NOI 2007 货币兑换Cash （cdq分治 or Splay）
在cdq分治之前，先用n^2的算法理一理题意。
Description
Input
第一行两个正整数N、S，分别表示小Y 能预知的天数以及初始时拥有的钱数。 接下来N 行，第K 行三个实数AK、BK、RateK，意义如题目中所述
Output
只有一个实数MaxProfit，表示第N 天的操作结束时能够获得的最大的金钱 数目。答案保留3 位小数。
Sample Input
3 100
1 1 1
1 2 2
2 2 3
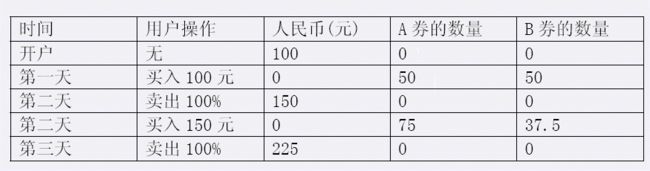
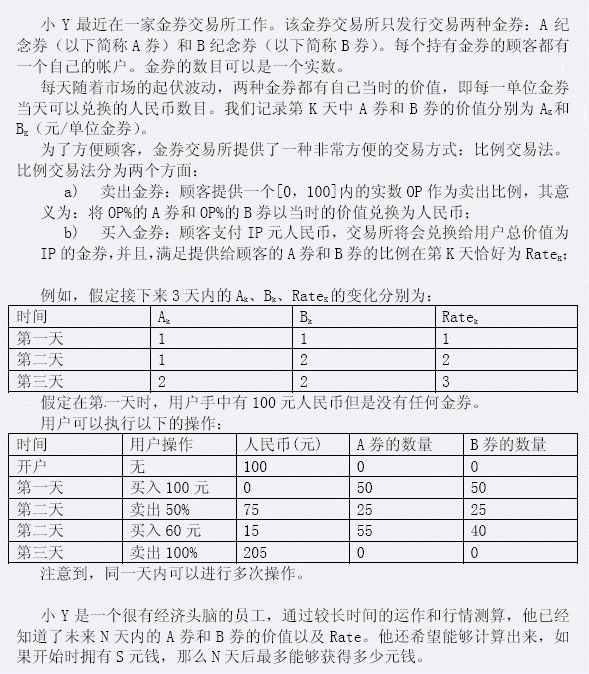
1 1 1
1 2 2
2 2 3
Sample Output
225.000
HINT
题解
只要记录第i天的最大价值为f[i]：
f[i] = max{f[i - 1], value(j, i) = (在第j天买光f[j]的钱,在第i天卖完所得的价值)}
在第j天卖光可以得到股票B的数量 nb = f[j] / (A[j] * Rate[j] + B[j])
在第j天卖光可以得到股票A的数量 na = nb * Rate[j]
所以value(j, i) = na * A[i] + nb * B[i];
复杂度O(n^2)，60分。代码长度 < 1kb
cdq的论文中是用f[i]记录第i天a股的个数，意思相同：
f [1]←S * Rate[1] / (A[1] * Rate[1] + B[1])
Ans←S
For i ← 2 to n
For j ← 1 to i-1
x ← f [j] * A[i] + f [j] / Rate[j] * B[i]
If x > Ans
Then Ans ← x
End For
f [i] ← Ans * Rate[i] / (A[i] * Rate[i] + B[i])
End For
Print(Ans)
Splay 强行维护一个凸包 可以过掉 由于Splay维护一个凸包 所以每次插入一个点都再处理一下这个点的左右是否仍然保持凸性，删除凸包内的点，也可能该点在凸包内就一次删掉了。（加了读入优化，可忽略）
图稍微盗几张放这里吧，凸性的一些证明详细这个链接， http://www.cppblog.com/zxytim/archive/2010/04/28/113854.html ，我是模仿这位菊苣的写的，由于抄的不留心导致debug了很久。
盗图部分，外链就是上面那条：
/*
观察可以发现，可以成为最大值的点一定是所有点在一象限以x递增，y递减的一些点构成的凸壳
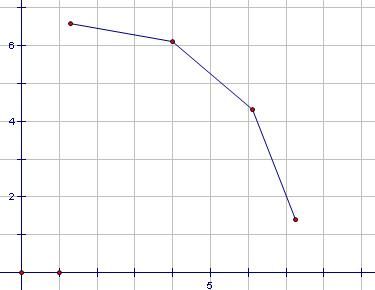
取得最大时：
所以我们要维护这个凸壳上的点。
插入时的维护：
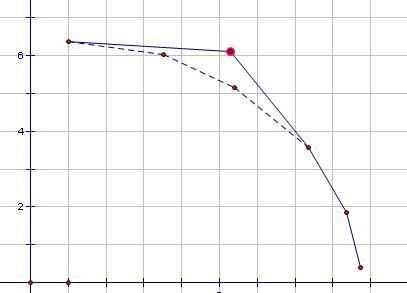
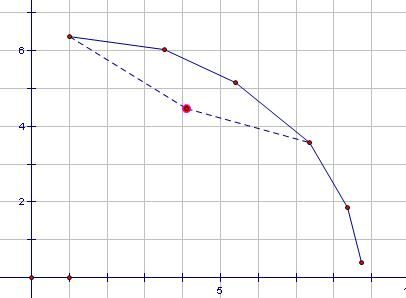
对一条斜率已知的直线查询时：
因为凸壳上斜率递减，所以可以通过对某个点与左右的点所构成直线的斜率进行判断：
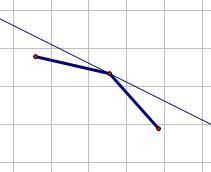
具体维护的时候为了达到较好的复杂度，要用平衡树维护。我选择了Splay，因为有些操作在Splay上面要方便些。。
*/
不懂伸展树进这里看，《算法合集之《伸展树的基本操作与应用》http://wenku.baidu.com/link?url=JznzcqFPVexmkM82og5ya1ui77gOyM105ETjqAp6V0tcUG8f08Tmc5D2DD2CUUmcuNwV3UZUtRv5idMwClHmhFI4ZaRzcEZtnzNQapOMyfe
代码这样：
/***********************************/
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
const int maxn = 100010;
#define REP(i,n) for(int i=0;i<n;i++)
#define FOR(i,l,r) for(int i=l;i<=r;i++)
#define INF 1e10
#define eps 1e-8
typedef double DB;
using namespace std;
/** I/O Accelerator Interface .. **/ //{
#define g (c=getchar())
#define d isdigit(g)
#define p x=x*10+c-'0'
#define n x=x*10+'0'-c
#define pp l/=10,p
#define nn l/=10,n
template<class T> inline T& RD(T &x){
char c;while(!d);x=c-'0';while(d)p;
return x;
}
inline DB& RF(DB &x){
//scanf("%lf", &x);
char c;while(g,c!='-'&&c!='.'&&!isdigit(c));
if(c=='-')if(g=='.'){x=0;DB l=1;while(d)nn;x*=l;}
else{x='0'-c;while(d)n;if(c=='.'){DB l=1;while(d)nn;x*=l;}}
else if(c=='.'){x=0;DB l=1;while(d)pp;x*=l;}
else{x=c-'0';while(d)p;if(c=='.'){DB l=1;while(d)pp;x*=l;}}
return x;
}
#undef nn
#undef pp
#undef n
#undef p
#undef d
#undef g
template<class T> inline void OT(const T &x){
printf("%.3lf\n", x);
}
template<class T> inline void checkMax(T &a,const T b){if (a<b) a=b;}
struct SplayNode{
int l, r, fa;
double x, y;
}node[maxn];
int tot=0;
inline double CrossProduct(double x0, double y0, double x1, double y1, double x2, double y2){
return (x1 - x0) * (y2 - y0) - (y1 - y0) * (x2 - x0);
}
inline double CrossProduct(int a, int b, int c){
return CrossProduct(node[a].x, node[a].y,
node[b].x, node[b].y,
node[c].x, node[c].y);
}
namespace SplayTree{
int root = 0;
inline void RightRotate(int x){
int l = node[x].l, fa = node[x].fa;
node[x].l = node[l].r; node[node[x].l].fa = x;
node[l].r = x; node[x].fa = l;
if (fa){
if (x == node[fa].l){
node[fa].l = l;
}
else{
node[fa].r = l;
}
}
node[l].fa = fa;
}
inline void LeftRotate(int x){
int r = node[x].r, fa = node[x].fa;
node[x].r = node[r].l; node[node[x].r].fa = x;
node[r].l = x; node[x].fa = r;
if (fa){
if (x == node[fa].l){
node[fa].l = r;
}
else{
node[fa].r = r;
}
}
node[r].fa = fa;
}
inline void Splay(int x, int FA){
int fa, Fa;
while(node[x].fa != FA){
fa = node[x].fa;
Fa = node[fa].fa;
if (Fa == FA){
if (x == node[fa].l)
RightRotate(fa);
else
LeftRotate(fa);
}
else{
if (x == node[fa].l){
if (fa == node[Fa].l){
RightRotate(Fa);
RightRotate(fa);
}
else{
RightRotate(fa);
LeftRotate(Fa);
}
}
else{
if (fa == node[Fa].r){
LeftRotate(Fa);
LeftRotate(fa);
}
else{
LeftRotate(fa);
RightRotate(Fa);
}
}
}
}
if (FA == 0)
root = x;
}
inline int Pred(int x){
if (node[x].l){
x = node[x].l;
while(1){
if (!node[x].r){
return x;
}
x = node[x].r;
}
}
else{
while(1){
if (node[x].fa){
if (x == node[node[x].fa].r){
return node[x].fa;
}
x = node[x].fa;
}
else{
return 0;
}
}
}
}
inline int Succ(int x){
if (node[x].r){
x = node[x].r;
while(1){
if (!node[x].l){
return x;
}
x = node[x].l;
}
}
else{
while(1){
if (node[x].fa){
if (x == node[node[x].fa].l){
return node[x].fa;
}
x = node[x].fa;
}
else{
return 0;
}
}
}
}
inline void Del(int now){
Splay(now, 0);
int pred = Pred(now), succ = Succ(now);
if (pred && succ){
Splay(pred, 0);
Splay(succ, root);
node[node[root].r].l = 0;
}
else if (pred && !succ){
Splay(pred, 0);
node[root].r = 0;
}
else if (!pred && succ){
Splay(succ, 0);
node[root].l = 0;
}
else{
root = 0;
}
}
inline void AdjustLeft(int now){
int p1, p2;
while(1){
p1 = Pred(now);
p2 = Pred(p1);
if (p1 && p2){
if(CrossProduct(p2, p1, now) >= 0 || node[p1].y <= node[now].y){
Del(p1);
}
else{
break;
}
}
else if(p1 && node[p1].y <= node[now].y){
Del(p1);
}
else{
break;
}
}
}
inline void AdjustRight(int now){
int p1, p2;
while(1){
p1 = Succ(now);
p2 = Succ(p1);
if (p1 && p2){
if(CrossProduct(now, p1, p2) >= 0){
Del(p1);
}
else{
break;
}
}
else{
break;
}
}
}
inline void Adjust(int now){
int pred = Pred(now); int succ = Succ(now);
if (pred && succ && CrossProduct(pred, now, succ) >= 0){
Del(now);
}
else if (succ && node[succ].y >= node[now].y){
Del(now);
}
else{
AdjustLeft(now);
AdjustRight(now);
}
}
inline void Insert(double x, double y){
int now = root, fa = 0, flag = 0;
while(1){
if (!now){
now = ++tot;
node[now].x = x, node[now].y = y;
node[now].fa = fa;
if (flag == 0){
node[fa].l = now;
}
else{
node[fa].r = now;
}
Splay(now, 0);
break;
}
else{
fa = now;
if (x <= node[now].x) now = node[now].l, flag = 0;
else now = node[now].r, flag = 1;
}
}
Adjust(root);
}
inline double Cal(double x, double y, double A, double B){
return A*x + B*y;
}
inline double Slope(double x, double y){
if (fabs(x) < eps){
return INF;
}
return y/x;
}
inline double getMax(double A, double B){
double k = -A/B;
double x, y;
int now = root;
while(1){
x = node[now].x; y = node[now].y;
int pred = Pred(now), succ = Succ(now);
if (!pred && !succ){
return Cal(x, y, A, B);
}
else if (pred && !succ){
if (k <= Slope(x - node[pred].x, y - node[pred].y)){
return Cal(x, y, A, B);
}
else{
if (node[now].l){
now = node[now].l;
}
else{
return Cal(x, y, A, B);
}
}
}
else if (!pred && succ){
if (k >= Slope(node[succ].x - x, node[succ].y - y)){
return Cal(x, y, A, B);
}
else{
if (node[now].r){
now = node[now].r;
}
else{
return Cal(x, y, A, B);
}
}
}
else{
double kl = Slope(x - node[pred].x, y - node[pred].y);
double kr = Slope(node[succ].x - x, node[succ].y - y);
if (kl >= k && k >= kr){
return Cal(x, y, A, B);
}
else if(k <= kr){
now = node[now].r;
}
else{
now = node[now].l;
}
}
}
}
}
int main(){
// freopen("data.in","r",stdin);
// freopen("data.out","w",stdout);
int n, s;
double ans, A, B, R;
RD(n); RD(s);
RF(A); RF(B); RF(R);
ans = s;
#define y (ans/(A*R+B))
#define x (y*R)
SplayTree::Insert(x,y);
FOR(i,2,n){
RF(A); RF(B); RF(R);
checkMax(ans, SplayTree::getMax(A, B));
SplayTree::Insert(x, y);
#undef x
#undef y
}
OT(ans);
return 0;
}
下面进入cdq分治
/********************************/