连连看游戏,2点是否可消除算法分析
现在在看郁金香的VC外挂教程,其中对于连连看外挂
在此感谢这位兄弟http://bbs.pediy.com/showthread.php?...8%8B+%E7%A8%8B
提供的下载地址,现在学习中……
言归正传,这个外挂的最难的就是检查2点是不是可以联通的算法,我们就来研究这一点
这个游戏,发现2点之间连接线段数需要满足 <= 3 这个条件
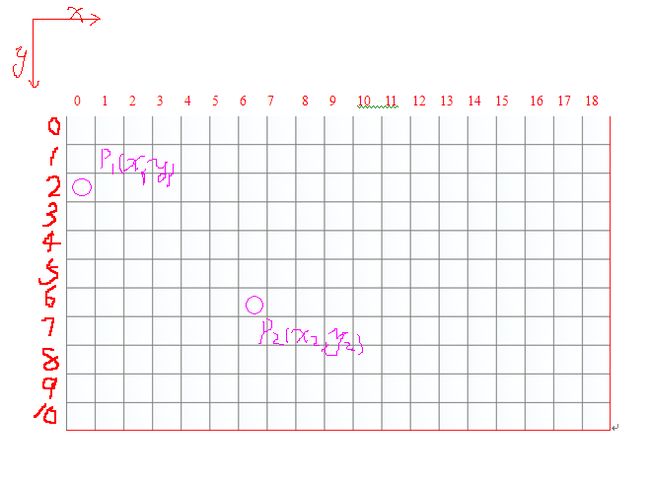
如图1:
我们先来谈谈3条线段的情况,先假设,棋盘上除了这2点以外全部为空,这2点分别用p1,p2表示,并显示坐标,那么在连接线段数<= 3 的情况下,一共有多少种路径呢?
如图2:
我们来思考一下,以下是所有路径,如图3:
(路径用绿线表示)可以看到这不是一两种的问题,而是由很多种,其中我用深颜色的线画出了几条有代表性的路径,
仔细的看图就会发现其中有规律可寻,看图4:

我标出了其中比较重要的4个点!~
这4个点分别是p1,p2在坐标轴上的投影,分别用 px1,px2(表示在x轴上的投影),py1,py2(表示y轴上的投影) 如图5:
先来分析px1,px2可以从图3上清楚的看到,联通路径上的有一部分就是就是线段px1,px2,或者是它的平行线!~
再分析py1,py2 也是一样的道理
我们再来分析一下px1,px2,py1,py2的坐标情况,如果已知p1(x1,y1),p2(x2,y2)的坐标,那么px1,px2,py1,py2坐标是什么呢?
只要有几何的初步知识就可以知道px1(x1,0),px2(x2,0),py1(0,y1),py2(0,y2)
那么分析上面的一大堆对于我们有什么用呢?
答案是肯定有用!~
看图6:
图中连通的路径由3条线段,有4个点组成,只要判断线段1,2,3,是否都连通,就可以判断2点是否可以连通了!~
实际上分析,每个人都可以分析的头头是道,编程最难的就是怎么样把分析好的数学模型通过编程来实现,分析是不需要考虑很多的细节问题的,而编程实现需要考虑很多的细节问题!~
那这样的话,就需要先写一个判断2点是否可以连通的函数了!~
好了我们下面来实现这个函数:
注:我用的是VC6.0
bool LineIfConnect(POINT Point1, POINT Point2, byte ChessData[10][18])
{
/* 功能 :检查Point1,Point2是否连通(2点之间连线的数值是不是为NULL,包括这2点自身)
*
* 参数1 :第1点
* 参数2 :第2点
* 对于参数的要求:Point1.x == Point2.x || Point1.y == Point2.y
* 参数3 :检测2点所在的数组(棋盘)
*
* 返回值 :true 表示可以连通,false 表示不可以连通
* */
int i;
if ((Point1.x == Point2.x) && (Point1.y != Point2.y)) // 横坐标相同,纵坐标不同
{
if (Point1.y < Point2.y) // point1 在 point2 上方
{
for (i = Point1.y; i <= Point2.y; i++) // for循环检测2点之间的所有元素
if (ChessData[i][Point1.x] != NULL)
return false;
}
else if (Point1.y > Point2.y) // point1 在 point2 下方
{
for (i = Point2.y; i <= Point1.y; i++) // for循环检测2点之间的所有元素
if (ChessData[i][Point1.x] != NULL)
return false;
}
}
else if ((Point1.x != Point2.x) && (Point1.y == Point2.y)) // 横坐标不同,纵坐标相同
{
if (Point1.x < Point2.x) // point1 在 point2 左边
{
for (i = Point1.x; i <= Point2.x; i++)
if (ChessData[Point1.y][i] != NULL)
return false;
}
else if (Point1.x > Point2.x) // // point1 在 point2 右边
{
for (i = Point2.x; i <= Point1.x; i++) // for循环检测2点之间的所有元素
if (ChessData[i][Point1.x] != NULL)
return false;
}
}
else if ((Point1.x == Point2.x) && (Point1.y == Point2.y)) // 2点为同一点的情况
return true;
else
return false;
return true;
}
bool DecideChessIfRemove(POINT Point1, POINT Point2, byte ChessData[10][18])
{
/* 功能 :检查Point1,Point2是否可以消除
*
* 参数1 :第1点
* 参数2 :第2点
* 参数3 :检测2点所在的数组(棋盘)
*
* 返回值 :true 表示可以消除,false 表示不可以消除
* */
int x1 = Point1.x;
int y1 = Point1.y; // Point1 == (x1, y1)
int x2 = Point2.x;
int y2 = Point2.y; // Point2 == (x2, y2)
int i, j;
POINT p1, p2;
byte point1 = ChessData[Point1.y][Point1.x];
byte point2 = ChessData[Point2.y][Point2.x];
ChessData[Point1.y][Point1.x] = ChessData[Point2.y][Point2.x] = NULL; // 2点在数组的位置设为NULL
p1.y = y1;
p2.y = y2;
for (i = 0; i <= 18; i++) // 横坐标在变 下面的两个for循环是关键,线段py1,py2在平移
{
p1.x = i; // p1 = (i, y1)
p2.x = i; // p2 = (i, y2)
if (LineIfConnect(p1, p2, ChessData))
if ((LineIfConnect(Point1, p1, ChessData)) && (LineIfConnect(Point2, p2, ChessData)))
{
ChessData[Point1.y][Point1.x] = point1;
ChessData[Point2.y][Point2.x] = point2;
return true;
}
}
p1.x = x1;
p2.x = x2;
for (j = 0; j <=10; j++) // 纵坐标在变 , 线段px1,px2 在平移
{
p1.y = j; // p1 = (x1, j)
p2.y = j; // p2 = (x2, j)
if (LineIfConnect(p1, p2, ChessData))
if ((LineIfConnect(Point1, p1, ChessData)) && (LineIfConnect(Point2, p2, ChessData)))
{
ChessData[Point1.y][Point1.x] = point1;
ChessData[Point2.y][Point2.x] = point2;
return true;
}
}
ChessData[Point1.y][Point1.x] = point1;
ChessData[Point2.y][Point2.x] = point2;
return false; // 没有找到连通的路径
}
好了函数的编写告一段落,实际 上写程序最为艰难就是调试阶段 了
来写一个程序测试一下:
#include <afxwin.h> // MFC core and standard components
#include <afxext.h> // MFC extensions
#include <afxdisp.h> // MFC Automation classes
#include <afxdtctl.h> // MFC support for Internet Explorer 4 Common Controls
#include <afxcmn.h> // MFC support for Windows Common Controls
#include <stdio.h>
#include <stdlib.h>
#include "function.h"
int main()
{
printf("开始 测试\r\n\n\n");
byte ChessData[10][18];
int i,j;
for (j = 0; j <= 10; j++)
{
for (i = 0; i <= 18; i++)
{
ChessData[j][i] = rand()%2;
printf("%2d ",ChessData[j][i]);
}
printf("\r\n");
}
POINT p1; // p1的位置
p1.x = 13;
p1.y = 5;
POINT p2; // p2的位置
p2.x = 14;
p2.y = 0;
if (DecideChessIfRemove(p1, p2, ChessData))
printf("2点相连\n\n");
else
printf("2点不相连!~\n\n");
for (j = 0; j <= 10; j++)
{
for (i = 0; i <= 18; i++)
{
printf("%2d ",ChessData[j][i]);
}
printf("\r\n");
}
return 0;
}
上面是可以联通的情况,那找一个不可以联通的情况试验一下:
#include <afxwin.h> // MFC core and standard components
#include <afxext.h> // MFC extensions
#include <afxdisp.h> // MFC Automation classes
#include <afxdtctl.h> // MFC support for Internet Explorer 4 Common Controls
#include <afxcmn.h> // MFC support for Windows Common Controls
#include <stdio.h>
#include <stdlib.h>
#include "function.h"
int main()
{
printf("开始 测试\r\n\n\n");
byte ChessData[10][18];
int i,j;
for (j = 0; j <= 10; j++)
{
for (i = 0; i <= 18; i++)
{
ChessData[j][i] = rand()%2;
printf("%2d ",ChessData[j][i]);
}
printf("\r\n");
}
POINT p1; // 这里改了
p1.x = 7;
p1.y = 7;
POINT p2; // 这里改了
p2.x = 10;
p2.y = 6;
if (DecideChessIfRemove(p1, p2, ChessData))
printf("2点相连\n\n");
else
printf("2点不相连!~\n\n");
for (j = 0; j <= 10; j++)
{
for (i = 0; i <= 18; i++)
{
printf("%2d ",ChessData[j][i]);
}
printf("\r\n");
}
return 0;
}
好了大功告成,说明我们的函数还是有些用的
最后感谢大家能看我一篇文章
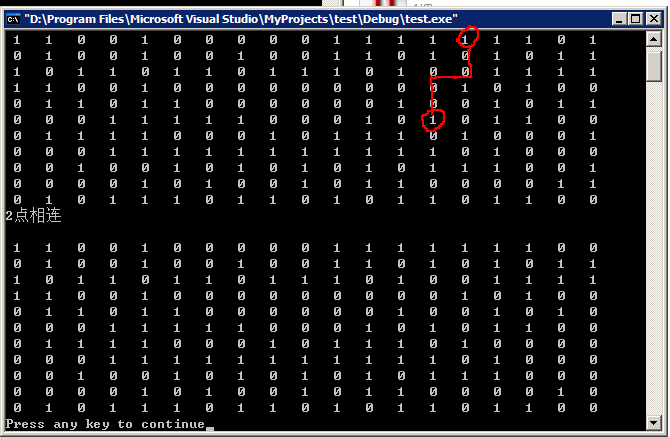
最后请看图9:

谁能给我分析一下,为什么2个图标红线处不一样呢?
我没有深入的进行调试,对不起了大家,如果用我的代码写外挂,有什么bug,我有免责申明啊