可扩展机器学习——梯度下降(Gradient Descent)
注:这是一份学习笔记,记录的是参考文献中的可扩展机器学习的一些内容,英文的PPT可见参考文献的链接。这个只是自己的学习笔记,对原来教程中的内容进行了梳理,有些图也是引用的原来的教程,若内容上有任何错误,希望与我联系,若内容有侵权,同样也希望告知,我会尽快删除。这部分本应该加上实验的部分,实验的部分在后期有时间再补上。
可扩展机器学习系列主要包括以下几个部分:
概述
- Spark分布式处理
- 线性回归(linear Regression)
- 梯度下降(Gradient Descent)
- 分类——点击率预测(Click-through Rate Prediction)
- 神经科学
四、梯度下降(Gradient Descent)
1、线性回归的优化问题
对于线性回归来说,其目标是找到一组 w∗ 使得下面的函数 f(w) 达到最小:
2、梯度下降法的流程
梯度下降法是一种迭代型的优化算法,根据初始点在每一次迭代的过程中选择下降法方向,进而改变需要修改的参数,梯度下降法的详细过程如下:
- Start at a random point
- Repeat
- Determine a descent direction
- Choose a step size
- Update
- Until stopping criterion is satisfied
具体过程如下图所示:
在初始时,在点 w0 处,选择下降的方向,选择步长,更新,此时到达 w1 处,判断是否满足终止的条件,发现并未到达最优解,重复上述的过程,直至到达 w∗ 。
3、凸优化与非凸优化
简单来讲,凸优化问题是指只存在一个最优解的优化问题,即任何一个局部最优解即为全局最优解,可以由下图表示:
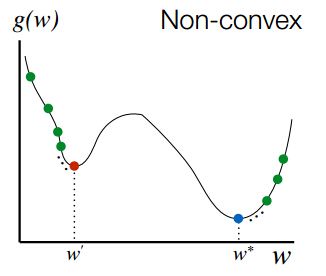
非凸优化是指在解空间中存在多个局部最优解,而全局最优解是其中的某一个局部最优解,可以由下图表示:
最小二乘(Least Squares),岭回归(Ridge Regression)和Logistic回归(Logistic Regression)的损失函数都是凸优化问题。
4、梯度下降法的若干问题
1、选择下降的方向
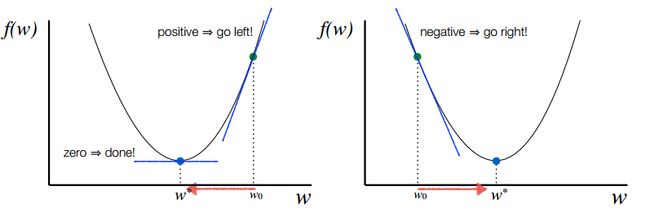
为了求解优化问题 f(w) 的最小值,我们希望每次迭代的结果能够接近最优价 w∗ ,对于一维的情况,如下图所示:
若当前点的斜率(梯度)为正,则选择的方向向左,若当前的斜率(梯度)为负,则选择的梯度的方向是向右。
负的斜率即为下降的方向。
对于上述的一维的情况,有下述的更新规则:
其中, αi 称为步长。对于二维的情况,如下图所示:
其中,函数值由黑白色表示,黑色表示更大的值,箭头表示的是梯度。
负的梯度是最快的下降的方向。
此时更新的规则如下:
2、最小二乘中的梯度下降
梯度下降法的更新规则如上所示,对于最小二乘法,有如下的损失函数的表示:
在利用梯度下降法的过程中需要求解梯度,即:
则根据更新公式,有如下的更新步骤:
对于向量形式,有:
3、步长的选择
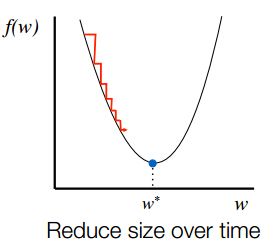
对于步长 α 的选择,若选择太小,会导致收敛的速度比较慢;若选择太大,则会出现震荡的现象,即跳过最优解,在最优解附近徘徊,上述两种情况如下面的两张图所示:
因此,选择合适的步长对于梯度下降法的收敛效果显得尤为重要。
在实践的过程中,人们发现了不同的步长形式,一种通用的步长设置方法如下:
其中, α 是一个常数, n 表示的是训练数据中特征的个数, i 表示的是迭代的代数。
4、梯度下降法的优缺点
对于梯度下降法,有如下的一些优缺点:
优点
- 容易并行
- 每次迭代过程中开销较小
- 随机梯度下降的开销更小
缺点
- 收敛速度较慢
- 需要在节点之间进行通信
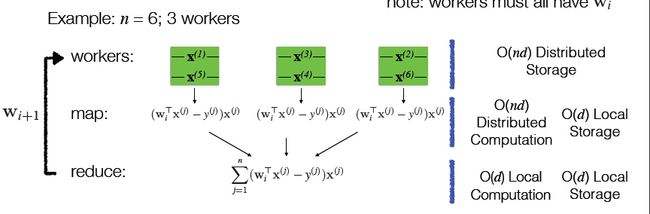
5、并行梯度下降
对于梯度下降法中的更新规则:
并行的计算方法如下:
若需要PDF版本,请关注我的新浪博客@赵_志_勇,私信你的邮箱地址给我。
参考文献
scalable-machine-learning