HDU-5521-Meeting【2015沈阳赛区】【最短路】

HDU-5521-Meeting

        Time Limit: 12000/6000 MS (Java/Others)    Memory Limit: 262144/262144 K (Java/Others)

Problem Description
Bessie and her friend Elsie decide to have a meeting. However, after Farmer John decorated his
fences they were separated into different blocks. John’s farm are divided into n blocks labelled from 1 to n.
Bessie lives in the first block while Elsie lives in the n-th one. They have a map of the farm
which shows that it takes they ti minutes to travel from a block in Ei to another block
in Ei where Ei (1≤i≤m) is a set of blocks. They want to know how soon they can meet each other
and which block should be chosen to have the meeting.

Input
The first line contains an integer T (1≤T≤6), the number of test cases. Then T test cases
follow.

The first line of input contains n and m. 2≤n≤105. The following m lines describe the sets Ei (1≤i≤m). Each line will contain two integers ti(1≤ti≤109) and Si (Si>0) firstly. Then Si integer follows which are the labels of blocks in Ei. It is guaranteed that ∑mi=1Si≤106.

Output
For each test case, if they cannot have the meeting, then output “Evil John” (without quotes) in one line.

Otherwise, output two lines. The first line contains an integer, the time it takes for they to meet.
The second line contains the numbers of blocks where they meet. If there are multiple
optional blocks, output all of them in ascending order.

Sample Input
2
5 4
1 3 1 2 3
2 2 3 4
10 2 1 5
3 3 3 4 5
3 1
1 2 1 2

Sample Output
Case #1: 3
3 4
Case #2: Evil John

Hint
In the first case, it will take Bessie 1 minute travelling to the 3rd block, and it will take Elsie 3 minutes travelling to the 3rd block. It will take Bessie 3 minutes travelling to the 4th block, and it will take Elsie 3 minutes travelling to the 4th block. In the second case, it is impossible for them to meet.

题目链接：HDU 5521

题目大意：A,B两个人分别在1和n区。给出区之间有联系的图以及到达所需时间。求两个人见面最短时间以及在哪个区碰面（可有多个）

题目思路：
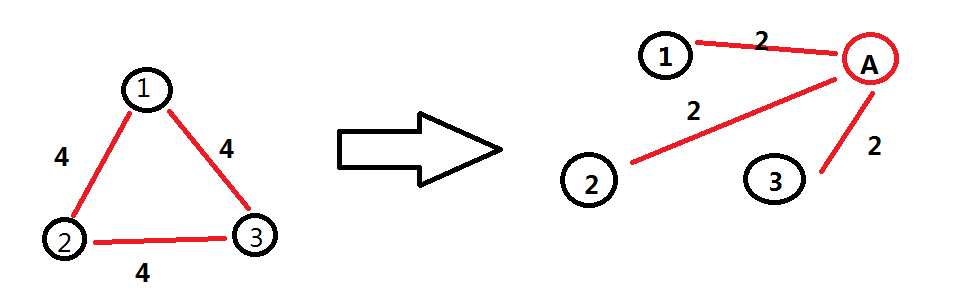
这道题难点在于建图，巧妙方法： 每个集合外虚建一个点Ai，然后，i集合里面的block到达A的距离为t/2。

                                    这样1->2也是4，很巧妙的减少了边。

考虑有浮点数误差，所以各点到A以t计算。最后结果除以2。

建图之后就是一道比较裸的最短路问题，用dijkstra分别求出1为起点和n为起点到各点的时间。第i点的时间为，time[i] = max（dist[0][i],dist[1][i]）;求出最小的time即可。

trick：

    1.点数N=n+2*最大集合数=1e5+2e6 
    2.边数M=3*最大集合数=3e6 
    3.要用LL存t和dist

以下是代码：

#include <vector>
#include <map>
#include <set>
#include <algorithm>
#include <iostream>
#include <cstdio>
#include <cmath>
#include <cstdlib>
#include <string>
#include <queue>
#include <cstring>
using namespace std;

/*=========================================*\ 复杂度：O（e * log e） INIT: 调用 init 初始化 CALL： dijkstra(n,start); dist[i] 为start到i的最短距离 \*=========================================*/ 
typedef long long LL;
int n,m;
vector <int> ans;
const LL INF = 0x3f3f3f3f3f;
const int MAXN = 3200010;
struct qnode
{
    int v;
    LL c;
    qnode (int _v = 0, LL _c = 0) : v(_v), c(_c) {}
    bool operator < (const qnode &r) const { return c > r.c; }
};
struct Edge
{
    int v;
    LL cost;
    Edge (int _v = 0,LL _cost = 0) : v(_v), cost (_cost){}
};
vector <Edge> E[MAXN];
bool vis[MAXN];
LL dist[2][MAXN];
void dijkstra(int n,int start,int poi) //点从编号1开始
{
    memset(vis,0,sizeof(vis));
    for (int i = 1; i <= MAXN; i++) dist[poi][i] = INF;
    priority_queue <qnode> que;
    while(!que.empty()) que.pop();
    dist[poi][start] = 0;
    que.push(qnode(start,0));
    qnode tmp;
    while(!que.empty())
    {
        tmp = que.top();
        que.pop();
        int u = tmp.v;
        if (vis[u]) continue;
        vis[u] = true;
        for (int i = 0; i < E[u].size(); i++)
        {
            int v = E[tmp.v][i].v;
            LL cost = E[u][i].cost;
            if (!vis[v] && dist[poi][v] > dist[poi][u] + cost)
            {
                dist[poi][v] = dist[poi][u] + cost;
                que.push(qnode(v,dist[poi][v]));
            }
        }
    }
}
void addedge(int u,int v,LL w)
{
    E[u].push_back(Edge(v,w));
}

int main(){
    int T;
    cin >> T;
    int cas = 1;
    while(T--)
    {
        for (int i = 0; i < MAXN; i++)
        {
            E[i].clear();
        }
        scanf("%d%d",&n,&m);
        int pos = n;    //用于记录新创建的点
        while(m--)
        {
            LL t;
            int s;
            scanf("%lld%d",&t,&s);
            pos++;
            while(s--)
            {
                int u;
                scanf("%d",&u);
                addedge(u,pos,t);
                addedge(pos,u,t);
            }
        } 
        dijkstra(pos,1,0);  //从1出发，结果保存在dist[0][]中 
        dijkstra(pos,n,1); //从n出发，结果保存在dist[1][]中 
        LL mindis = INF;
        ans.clear();
        for (int i = 1; i <= n; i++)
        {
            mindis = min(mindis,max(dist[0][i],dist[1][i]));
        }
        if (mindis == INF) printf("Case #%d: Evil John\n",cas++);
        else
        {
            printf("Case #%d: %lld\n",cas++,mindis / 2);
            for (int i = 1; i <= n; i++)
            {
                if (mindis == max(dist[0][i],dist[1][i]))
                {
                    ans.push_back(i);
                }
            }
            printf("%d",ans[0]);
            for (int i = 1; i < ans.size(); i++)
            {
                printf(" %d",ans[i]);
            }
            printf("\n");
        }      
    } 
    return 0;
}