ural1519之插头DP
1519. Formula 1
Time limit: 1.0 second
Memory limit: 64 MB Background
Regardless of the fact, that Vologda could not get rights to hold the Winter Olympic games of 20**, it is well-known, that the city will conduct one of the Formula 1 events. Surely, for such an important thing a new race circuit should be built as well as hotels, restaurants, international airport - everything for Formula 1 fans, who will flood the city soon. But when all the hotels and a half of the restaurants were built, it appeared, that at the site for the future circuit a lot of gophers lived in their holes. Since we like animals very much, ecologists will never allow to build the race circuit over the holes. So now the mayor is sitting sadly in his office and looking at the map of the circuit with all the holes plotted on it.
Problem
Who will be smart enough to draw a plan of the circuit and keep the city from inevitable disgrace? Of course, only true professionals - battle-hardened programmers from the first team of local technical university!.. But our heroes were not looking for easy life and set much more difficult problem: "Certainly, our mayor will be glad, if we find how many ways of building the circuit are there!" - they said.
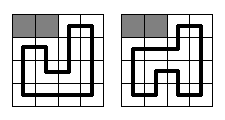
It should be said, that the circuit in Vologda is going to be rather simple. It will be a rectangle
N*
M cells in size with a single circuit segment built through each cell. Each segment should be parallel to one of rectangle's sides, so only right-angled bends may be on the circuit. At the picture below two samples are given for
N =
M = 4 (gray squares mean gopher holes, and the bold black line means the race circuit). There are no other ways to build the circuit here.
Input
The first line contains the integer numbers
N and
M (2 ≤
N,
M ≤ 12). Each of the next
N lines contains
M characters, which are the corresponding cells of the rectangle. Character "." (full stop) means a cell, where a segment of the race circuit should be built, and character "*" (asterisk) - a cell, where a gopher hole is located.
Output
You should output the desired number of ways. It is guaranteed, that it does not exceed 2
63-1.
Samples
|
分析看这(转):http://blog.sina.com.cn/s/blog_51cea4040100gmky.html
按照上面链接分析就很明确了,情况分清楚了就好写了
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <string>
#include <queue>
#include <algorithm>
#include <map>
#include <cmath>
#include <iomanip>
#define INF 99999999
typedef long long LL;
using namespace std;
const int MAX=300000+10;//最多的有效状态
const int N=10+10;
int n,m,size,index;
int mp[N][N],total[2],bit[N],ex,ey;//ex,ey记录最后一个非限制点,total记录有多少状态
int head[MAX],Next[MAX],Hash[MAX];//Hash用哈希查询状态,才用邻接表查询
//对于第i,j格只需要用到第i,j-1格到达,所以才用滚动数组节省内存
LL dp[2][MAX],state[2][MAX],sum;//state记录相应状态,dp记录相应状态可到达的数量
void Init(){
memset(mp,0,sizeof mp);
sum=size=index=0;
total[index]=1;
state[index][1]=0;//初始化只有一种可到达状态:没有任何插头
dp[index][1]=1;
}
void HashCalState(LL s,LL num){
int pos=s%MAX;
for(int i=head[pos];i != -1;i=Next[i]){
if(state[index][Hash[i]] == s){
dp[index][Hash[i]]+=num;
return;
}
}
++total[index];
state[index][total[index]]=s;
dp[index][total[index]]=num;
//头插法
Hash[size]=total[index];
Next[size]=head[pos];
head[pos]=size++;
}
void DP(){//才用4进制进行DP,x*4^y=x*2^(2*y)
for(int i=1;i<=n;++i){
for(int k=1;k<=total[index];++k)state[index][k]<<=2;//由上移一行到达这一行(i,0格)在上一行的0号插头前面再加一个插头,去掉最后一个插头(最后一个插头肯定为0)
for(int j=1;j<=m;++j){//求由i,j-1到达i,j的状态以及状态数
memset(head,-1,sizeof head);
size=0;
index=index^1;
total[index]=0;
for(int k=1;k<=total[index^1];++k){//枚举上一格的状态,用来到达i,j某个状态
LL s=state[index^1][k];//取状态
LL num=dp[index^1][k];//取到达相应状态个数
int p=(s>>bit[j-1])%4;//取第j位
int q=(s>>bit[j])%4;//取第j+1位
if(!mp[i][j]){//i,j有限制不能通过,必须绕过
if(p+q == 0)HashCalState(s,num);//只有p=q=0才能到达p'=q'=0的状态,才用哈希计算到达的状态以及个数
}else if(p+q == 0){//i,j无限制则必须有两个插头通过(一进一出)
if(!mp[i+1][j] || !mp[i][j+1])continue;
s=s+(1<<bit[j-1])+2*(1<<bit[j]);//创建新的连通块(增加第j,j+1个插头)
HashCalState(s,num);
}else if(!p && q){//p无插头,q有插头,则新状态需要增加一个插头
if(mp[i][j+1])HashCalState(s,num);//状态不变,连通块不变
if(mp[i+1][j]){
s=s+q*(1<<bit[j-1])-q*(1<<bit[j]);
HashCalState(s,num);
}
}else if(p && !q){//同上
if(mp[i+1][j])HashCalState(s,num);
if(mp[i][j+1]){
s=s-p*(1<<bit[j-1])+p*(1<<bit[j]);
HashCalState(s,num);
}
}else if(p+q == 2){//p=q=1,合并连通块
int b=1;
for(int t=j+1;t<=m;++t){//寻找最近的匹配的括号
int v=(s>>bit[t])%4;
if(v == 1)++b;
if(v == 2)--b;
if(b == 0){
s=s+(1<<bit[t])-2*(1<<bit[t]);//将右括号变为左括号
break;
}
}
s=s-(1<<bit[j-1])-(1<<bit[j]);
HashCalState(s,num);
}else if(p+q == 4){//p=q=2,同上
int b=1;
for(int t=j-2;t>=0;--t){//寻找最近的匹配括号
int v=(s>>bit[t])%4;
if(v == 2)++b;
if(v == 1)--b;
if(b == 0){
s=s-(1<<bit[t])+2*(1<<bit[t]);//将左括号变为右括号
break;
}
}
s=s-2*(1<<bit[j-1])-2*(1<<bit[j]);
HashCalState(s,num);
}else if(p == 1 && q == 2){//合并连通块,只有最后一格的时候才连成整个回路
if(i == ex && j == ey)sum+=num;
}else if(p == 2 && q == 1){
s=s-2*(1<<bit[j-1])-(1<<bit[j]);
HashCalState(s,num);
}
}
}
}
}
int main(){
char ch;
for(int i=0;i<N;++i)bit[i]=i<<1;//求4进制的某位用2进制求需要右移的位数*2
while(~scanf("%d%d",&n,&m)){
Init();
for(int i=1;i<=n;++i){
getchar();
for(int j=1;j<=m;++j){
scanf("%c",&ch);
mp[i][j]=(ch == '.');
if(ch == '.')ex=i,ey=j;
}
}
DP();//插头DP
printf("%lld\n",sum);
}
return 0;
}
/*
12 12
............
............
............
............
............
............
............
............
............
............
............
............
9 10
..........
..........
..........
..........
..........
..........
..........
..........
..........
*/