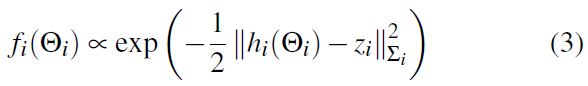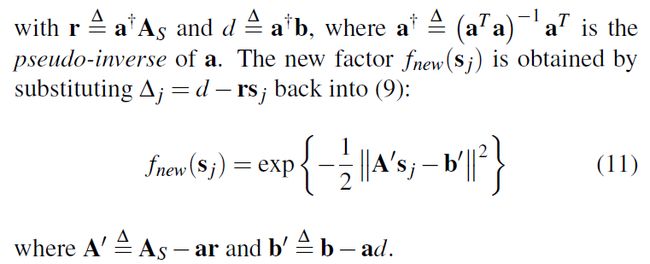iSAM2 笔记

摘要

iSAM2 将图优化问题转换成 Bayes tree 的建立、更新和推理问题。原始待优化的问题用 factor graph 表示，factor graph -> Bayes net 建立变量的条件概率，Bayes net -> Bayes tree 建立变量间的更新关系，Bayes tree 从 leaves 到 root 建立的过程，定义了变量逐级更新的 functions，Bayes tree 从 root 到 leaves 可以逐级更新变量值。iSAM2 整套架构建立在概率推理的基础上，和 iSAM 利用 QR 矩阵分解，当有 new factor 时，更新 R 矩阵差别蛮大。

感谢肖师兄讨论

factor grpah

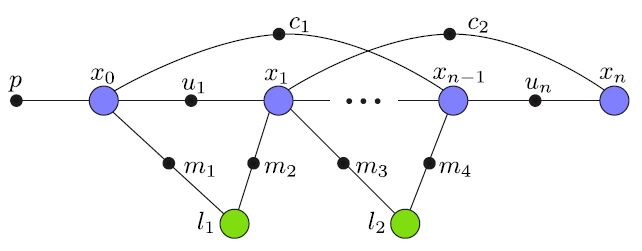
factor graph 结构如下：

在 SLAM 系统中通常假设 Gaussian measurement error 如下图所示：

SLAM 中的 pose 和 landmark 优化问题可以转化为图优化问题，在上图 factor graph 中：
xi 表示相机的 pose， li 表示 landmark point 坐标， xi 和 li 是 factor graph 中待求解的 variable。

ui 表示测量的相机两帧之间的位姿关系， mi 表示在相应相机位姿视角下对特征点的测量， p 是预先输入的 x0 的变量值，在 SLAM 系统中 x0 起到定义坐标系的作用。

SLAM 通常假设 Gaussian measurement model，factor graph 目标函数定义如下：

通过对变量线性化化简上式可得：

化简过程参见 iSAM 附录。

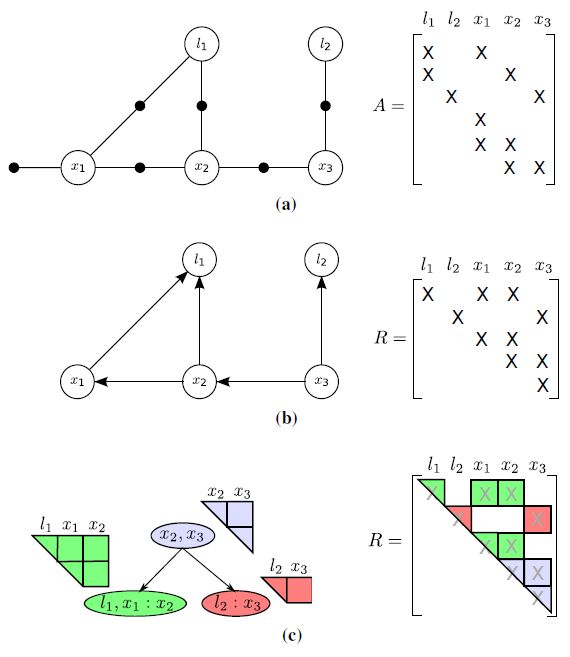
上式中的 A 矩阵，和 factor graph 中形式对应，如上图 (a) 所示，在 A 矩阵中，每个 factor 对应 A 矩阵的一行，factor 中包含到的变量在 A 矩阵中为非 0 元素，A 矩阵的非 0 元素是 factor 对变量一阶求导线性化得到。

上图中 (b) 矩阵 B 对应 factor graph A 矩阵消元后的结构，factor graph 每次消去一个变量，消去的变量在 square root R 中占据一行，最后的 R 矩阵的行列数等于变量的个数。这里的 R 矩阵只是个图示，在 iSAM2 实际求解过程中没有用到 iSAM 算法中 A 矩阵 QR 分解到的 R 矩阵。

根据 factor graph 构建的 Bayes tree 形式如 (c) 所示，(c) 中所示的 Bayes tree 和 R 矩阵成对应，重申一遍，这里 R 只是拿来做类比，在 iSAM2 求解过程中和 R 矩阵并无关系。

对于公式 5 的求解可以用 QR 或者 Cholesky 分解算法，流程如下：

factor graph -> Bayes net

作者原话 ”A crucial insight is that inference can be understood as converting the factor graph to a Bayes net using the elimination algorithms“

factor graph 中变量求解的转换成，factor graph 从 leaves 到 root 构建 Bayes tree，建立更新的 functions，和 Bayes tree 从 root 到 leaves 变量更新的过程。

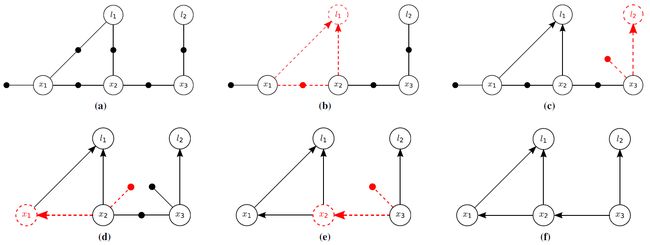
factor graph 变量消去过程如下图所示：

消去算法如下：

上图中 (a) 是原始的 factor graph，(b) (c) (d) (e) (f) 分别对应消去变量 l1 l2 x1 x2 x3 时的 factor graph。

factor graph 消元的过程看 Kaess 视频和 ppt，Kaess 视频 youtube 链接：
https://www.youtube.com/watch?v=_W3Ua1Yg2fk
视频 ppt 作者主页上可以找到。

factor graph 在消元过程中会建立变量的条件概率，例如对于变量 Δj 消元，和变量 Δj 相连的 factor 可以通过化简可以得到如下公式 (9)，当和变量 Δj 相连的变量已知时，可以得到公式 (10)，消去 Δj 得到和 Δj 相关联的变量之间的联合概率密度如公式 (11) 所示，同时 factor graph 消去变量还建立了消去的变量的更新公式，如公式 (12) 所示。

通过 factor graph 消元建立了变量的条件概率密度 P(θj|Sj) ，其中 θj 是待消去的变量， Sj 是和 θj 在 factor graph 相关联的变量。还同时建立了 Sj 的概率密度 fnew(θj) ，和待消去变量的更新关系（公式12）

后续会根据 factor grpah 消元产生的 P(θj|Sj) 和 fnew(θj) 建立 Bayes tree，Bayes tree 建立的过程实际是建立了变量的更新过程。

如上原文红色下划线描述，求解过程是 Bayes net 转化 Bayes tree，从树的低端开始到树的顶端构建变量之间的更新的 functions，然后再从树的顶端开始，根据公式 (12) 求解变量的最优值。

Bayes net -> Bayes tree

从 Bayes net 到 Bayes tree 构建过程如下，看Kaess 视频容易理解。

Bayes tree clique 中条件概率和变量间的更新关系，是根据前面 factor graph 到 Bayes net 转换时生成的条件概率和变量更新公式计算得到的，Bayes tree 实际建立了从根节点到叶子节点变量的更新关系。

Incremental inference

作者原文：”When a new measurement is added, for example a factor f′(xj,xj′) , only the paths between the cliques containing xj and xj′ and the root are affected. The sub-trees below these cliques are unaffected, as are any other sub-trees not containing xj or xj′ . The affected part of the Bayes tree is turned to a factor graph and the new factors are added to it. Using a new elimination order new factors are added to it. “

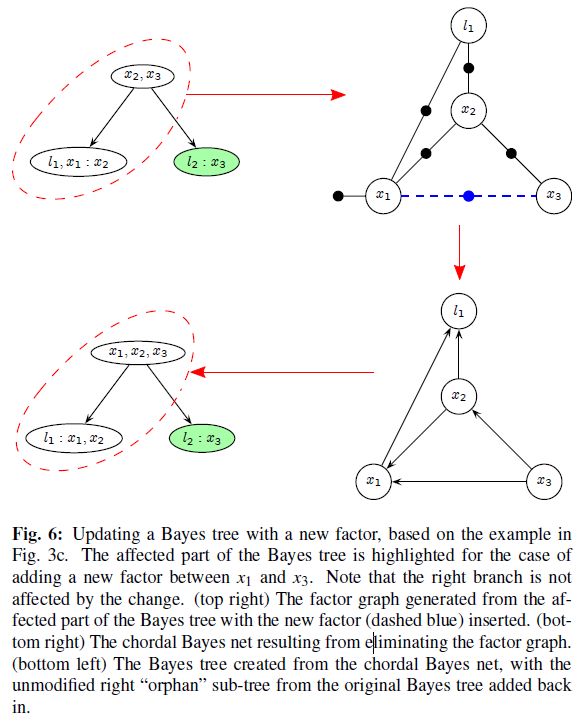
在添加一个新的 factor 时，例如在 xj 和 xj′ 之间添加一个新的 factor，只是 xj 和 xj′ 之间的 clique 和它们的 ancestor clique 会受影响，受影响的 clique 会在 Bayes tree 中重新拿出来，重新组合，组合完之后再把没有受到影响的 sub_trees 挂到重新组合后的 clique 下面。

更新完 Bayes tree 的结构后，从 root 出发到 leaves 还会逐级向下更新 clique 中的变量的值，相当于根据获取到的当前帧的信息，更新变量的值。作者视频中说从 root 向下更新的时候，如果变量值改变的较小，则停止更新，不再向下传播，但是代码中说，如果持续的不继续向下更新，误差会逐步累积。

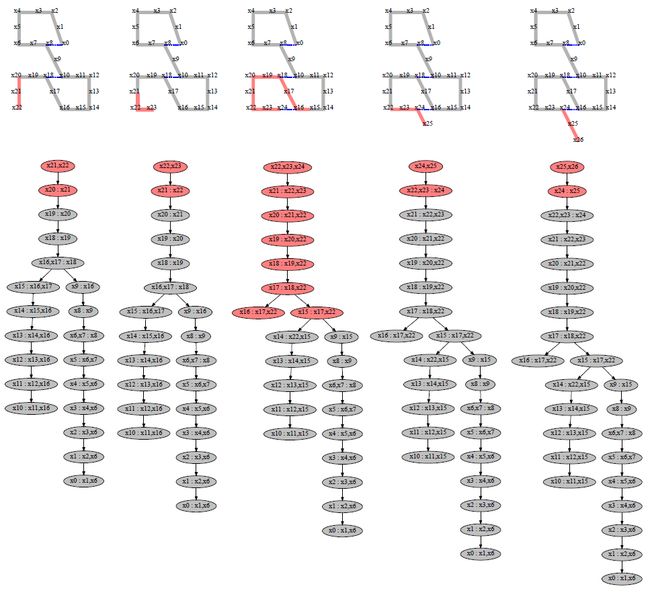
同样更新效果如下图，更新的时候，如果不存在回环更新只会牵扯到 root 附近的 clique，当存在回环时，牵扯到的 clique 较多，更新起来也相对更复杂。

当有新的 factor 时更新的 Bayes tree 方式如下：

Incrementtal variabl ordering

iSAM 对矩阵 QR 分解的时候，要有一个好的 variable ordering，一个好的 ordering 会减少矩阵分解的 fill-in，在 Bayes tree 中，fill-in translate to larger clique sizes，导致 clique 中变量个数太多，这点从变量更新的推导应该可以看出来（我自己还未仔细推导）。

对于 Bayes tree 来说每次更新的时候都可以对 Bayes tree 进行 reorder，”The affected part of the Bayes tree, for which variables have to be reordered, is typically small, as new measurements usually only affect a small subset of the overall state space represented by the variables of the estimation problem.”

和 iSAM 一样作者也是用 COLAMD 进行 reorder，COLAMD 论文读起来好吃力，请大神指教。

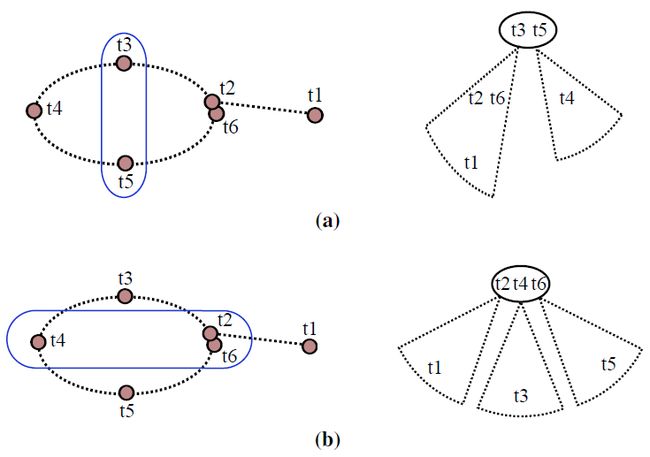
在 Bayes tree 中的变量进行 reorder 的时候，把新加入的变量放到树的 root 端会减少后续 Bayes tree 更新的计算量。作者举了个例子，如下：

在 (a) 和 (b) 中，新加入一个变量 t6 ， t2 和 t6 表示存在一个回环，(a) 表示不接受这个回环，如果不接收回环 t6 和 t5 有连接，更新的结果是 t6 挂在叶子节点上；(b) 表示接收回环，如果接收回环 t6 会和 t2 、 t5 相连接，更新的结果是，把 t6 放到 Bayes tree 的 root 节点上。两种更新对于 Bayes tree 的 fill in 是等价的，但是 (b) 把变量 t6 放到叶子节点上，使得下次添加和 t6 相关联的 factor 或者变量时，计算量减少。单纯使用 COLAMD reorder 不会考虑到这一点，作者提出使用 constrained COLAMD 进行更新，作者原话：”We use the constrained COLAMD (CCOLAMD) algorithm to both force the most recently accessed variables to the end and still provide a good overall ordering”

The iSAM2 Algorithm

作者原话：”We have already shown how the Bayes tree is updated with new liner factors. That leaves the question of how to deal with nonlinear factors and how to perform this process efficiently by only relinearizing where needed, a process that we call fluid relinearization. To further improve efficiency we restrict the state recovery to the variables that actually change, resulting in partial state updates”
因为在 SLAM 中要解决的是 nonlinear factors，需要对 nonlinear factors 线性化进行求解，作者提出跟踪实际变化的变量，只对实际变化的变量进行线性化 。

Fluid Relinearization

算法如下所示：

当添加新的 factor，Bayes tree 从 root 向 leaves 更新时，会根据公式 (12)，计算变量更新量，判断变量是否做更新 Alg. 5：
1、如果对变量的更新量大于一定阈值，对变量 mark
2、根据计算的更新量 Δj 对变量值进行更新
3、对 clique 中存在 marked variable 的 clique，和它们的 ancestor clique（一直到 root clique）的 clique 做 mark（因为这里需要对变量重新线性化，重新线性化的值，会对所有的 ancestors 的值有影响，Bayes tree 建立了自下到上的依赖关系）。

对于包含需要重新线性化的所有的 clique，和包含变量 clique 的父节点的 cliques（一直到 root clique），都需要根据 factor graph 重新消去变量重新计算变量间的更新关系，作者原话：”Caching those marginal factors during elimination allows restarting of the elimination process from the middle of the tree, rather than having to re-eliminate the complete system”

保存上一次消元时的中间结果，只需要从最下面一个受影响需要更新的 clique 开始重新线性化就好，不需要对整个 Bayes tree 都做线性化。

Partial State Updates

如上作者指出每次添加新的 factor 时，对于 Bayes tree 中变量不需要逐个都更新，只需要更新那些真的 change 的变量的就可以，可以想象在重建一个有多个房间的大的建筑物时，在一个房间中测量的结果，不会影响到其它几个房间中的变量，作者用 Partial state update 的方式，减少更新的变量的个数，算法如下：

算法 7 中要注意的一点如下图红色下划线所示：

这里改变量是指“更新量的改变量“，相当于二阶导数，因为上文中提出，当变量的更新量 Δ 超过一定阈值时，对变量重新线性化，也就说 Δ 值可能很大，所以这里判断变量更新的条件是如果 Δ 的改变量超过一定阈值时，才会对变量做更新。

变量更新是一个不断向下传播的过程，在 Bayes tree 中如果当前级变量判断不需要做更新了，当前级之后的变量也不需要做更新了。

Algorithm and Complexity

算法的整体框架 Alg. 8 所示，”The goal of our algorithm is to obtain an estimate θ for the variables(map and trajectory), given a set of nonlinear factors. New factors can arrive at any time and may add new variables to the estimation problem. Based on the current linearization point we solve a linearized systemas a subroutine in an iterative nonlinear optimization scheme. The linearized system is represented by the Bayes tree“

参考文献：
“iSAM2: Incremental Smoothing and Mapping Using the Bayes tree”
“iSAM: Incremental Smoothing and Mappint”