Kmeans和GMM参数学习的EM算法原理和Matlab实现

本文整理自JerryLead的博文“《K-means聚类算法》 ”，“《（EM算法）The EM Algorithm 》”，“《混合高斯模型（Mixtures of Gaussians）和EM算法 》”，以及自己编写的关于GMM的Matlab实现。
好的博文还有：
pluskid的《漫谈 Clustering (3): Gaussian Mixture Model》和《漫谈 Clustering (番外篇): Expectation Maximization》。

K-means和EM

K-means是聚类算法中最简单的一种，但是里面包含的思想却是不一般。聚类属于无监督学习，朴素贝叶斯、SVM等都是有类别标签 y 的，即已经给出了样本的分类。而聚类的样本中却没有给定 y ，只有特征 x 。聚类的目的是找到每个样本 x 潜在的类别 y ，并将同类别 y 的样本 x 放在一起。
在聚类问题中，给定训练样本 {xi}Ni=1 ，每个 xi∈Rn ，没有类别标签 y 。
K-means算法是将样本聚类成 K 个簇（cluster），具体算法描述如下：

1、随机选取 K 个聚类质心点为 {μk}Kk=1,μk∈Rn 。
2、重复下面过程直到收敛{
对于每一个样例 i ，计算其应该属于的类

zi=argminj||xi−μj||2

对于每一个类 j ，重新计算该类的质心

μj=∑Ni=11{zi=j}xi∑Ni=11{zi=j}

}

其中， K 是事先给定的聚类数， zi∈1,2,..,K 代表样例 i 与 K 个类中距离最近的那个类， μj 代表对属于同一个类的样本的质心。要将所有的样本聚成 K 类，首先随机选取 K 个点作为 K 个类的质心，第一步对于每一个样本计算其到 K 个质心的距离，选取距离最近的那个类作为 zi （经过第一步每个样本都有了所属的类）；第二步对于每一个类，重新计算它的质心 μj （对里面所有的样本坐标求平均）。重复迭代第一步和第二步直到质心不变或者变化很小。
K-means如何保证收敛?
K-means算法中强调结束条件就是收敛，可以证明的是K-means完全可以保证收敛性。下面定性的描述一下收敛性，定义畸变函数：

J(z,μ)=∑i=1N||xi−μzi||2

函数 J 表示每个样本点到其质心的距离平方和。K-means就是要将 J 调整到最小。假设当前 J 没有达到最小值，那么可以首先固定每个类的质心 μj ，调整每个样例的所属类别 zi 来让 J 函数减少，同样固定 zi ，调整 μj 也可以使 J 减小。这两个过程就是内循环中使 J 单调递减的过程。当 J 递减到最小时， μ 和 z 也同时收敛。由于畸变函数 J 是非凸函数，意味着不能保证取得的最小值是全局最小值，也就是说K-means对质心初始位置的选取比较敏感，但一般情况下K-means达到的局部最优已经满足需求。
K-means与EM的关系
K-means算法目的是将样本分成 K 个类，即求每个样例 x 的隐含类别 y ，然后利用隐含类别将 x 归类。由于事先不知道类别 y ，那么可以先对每个样例假定一个 y ，但是怎么知道假定的对不对呢？怎么评价假定的好不好呢？在此，可以使用样本的极大似然估计来度量，即 x 和 y 的联合分布 p(x,y) 。如果找到的 y 能够使 p(x,y) 最大，那么找到的 y 就是样例 x 的最佳类别， x 同时就聚类了。但是第一次指定的 y 不一定会让 p(x,y) 最大，而且 p(x,y) 还依赖于其他未知参数。当然在给定 y 的情况下，可以调整其他参数让 p(x,y) 最大；调整完参数后，发现有更好的 y 可以指定，那么重新指定 y 。反复迭代直至没有更好的 y 可以指定。
这个过程有几个难点：第一，怎么假定 y ？是每个样例硬指派一个 y 还是不同的 y 有不同的概率，概率如何度量？第二，如何估计 p(x,y) ， p(x,y) 还可能依赖很多其他参数，如何调整里面的参数让 p(x,y) 最大。
这可以采用EM的思想解决，E步就是估计隐含类别 y 的期望值，M步调整其他参数使得在给定类别 y 的情况下，极大似然估计 p(x,y) 能够达到极大值。然后在其他参数确定的情况下，重新估计 y ，周而复始，直至收敛。
对应于K-means，最开始对于每个样例 xi 随便指定一个 zi ，然后为了让 p(x,y) 最大（让 J 最小），求给定 zi 情况下最小时的 μj （前面提到的其他未知参数），然而此时发现，可以有更好的 zi （质心与样例 xi 距离最小的类别）指定给样例 xi ，那么 zi 得到重新调整，上述过程就开始重复了，直到没有更好的 zi 指定。可见K-means里体现了EM思想，E步是确定隐含类别变量 z ，M步更新其他参数 μ 来使 J 最小化。K-means隐含类别变量指定方法比较特殊，属于硬指定，即从 K 个类别中硬选出一个给样例，而不是对每个类别赋予不同的概率。总体思想还是一个迭代优化过程，有目标函数，也有参数变量，只是多了个隐含变量，确定其他参数估计隐含变量，再确定隐含变量估计其他参数，直至目标函数最优。

EM算法

下面介绍EM的整个推导过程：

Jensen不等式

设 f 是定义域为实数的函数，如果对于所有的实数 X ， f′′(x)≥0 ，那么 f 是凸函数。当 x 是向量时，如果其Hessian矩阵 H 是半正定的，那么 f 是凸函数。如果 f′′(x)>0 ，那么称 f 是严格凸函数。
Jensen不等式表述如下：如果 f 是凸函数， X 是随机变量，那么

E[f(x)]≥f(E[X])

特别地，如果 f 是严格凸函数，那么 E[f(x)]=f(E[X]) 当且仅当 p(x=E(X))=1 ，也就是说 X 是常量。
如果用图表示会很清晰：

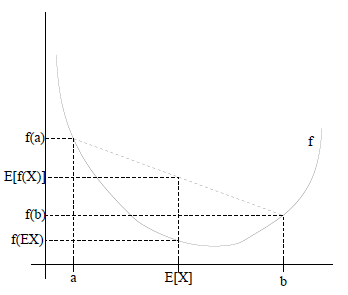
图中实线 f 是凸函数， X 是随机变量，有0.5的概率是a，有0.5的概率是b， X 的期望值就是a和b的中值了，图中可以看到 E[f(x)]≥f(E[X]) 成立。
当 f 是（严格）凹函数当且仅当 −f 是（严格）凸函数。
Jensen不等式应用于凹函数时，不等号方向反向，即 E[f(x)]≤f(E[X]) 。

EM算法

给定独立同分布训练样本 {xi}Ni=1 ，寻找到每个样例隐含的类别 z ，能使得 p(x,z) 最大。 p(x,z) 的最大似然估计如下：

L(θ)=∑i=1Nlogp(xi;θ)=∑i=1Nlog∑zip(xi,zi;θ)

该式直接求 θ 一般比较困难，因为有隐藏变量 z 存在，但是一般确定了 z 后，求解就容易了。
EM是一种解决存在隐含变量优化问题的有效方法。既然不能直接最大化 L(θ) ，那么就不断地建立 L(θ) 的下界（E步），然后优化下界（M步）。即对于每一个样例 i ，让 Q(zi) 表示该样例隐含变量 zi 的某种分布，且 ∑ziQ(zi)=1 ， Q(zi)≥0 。由Jensen不等式得：

L(θ)=∑i=1Nlog∑zip(xi,zi;θ)=∑i=1Nlog∑ziQ(zi)p(xi,zi;θ)Q(zi)≥∑i=1N∑ziQ(zi)logp(xi,zi;θ)Q(zi)

其中， log(x) 是凹函数且 ∑ziQ(zi)p(xi,zi;θ)Q(zi)
是 [p(xi,zi;θ)/Q(zi)] 的期望。
这个过程可以看作是对 L(θ) 求了下界。对于 Q 的选择，有多种可能，那种更好的？假设 θ 已经给定，那么 l(θ) 的值就决定于 Q(zi) 和 p(xi,zi) 了。通过调整这两个概率使下界不断上升，以逼近 L(θ) 的真实值，那么什么时候算是调整好了呢？当不等式变成等式时，说明调整后的概率能够等价于 L(θ) 。按照这个思路，要找到等式成立的条件。根据Jensen不等式，要想让等式成立，需要让随机变量变成常数值，即：

p(xi,zi;θ)Q(zi)=c

其中， c 为常数，不依赖于 zi 。由于 ∑zQ(z)=1 ，所以 ∑zip(xi,zi;θ)=1 ，（多个等式分子分母相加不变，这个认为每个样例的两个概率比值都是 c ），那么有下式：

Q(zi)=p(xi,zi;θ)∑zp(xi,z;θ)=p(xi,zi;θ)p(xi;θ)=p(zi|xi;θ)

至此，导出了在固定其他参数 θ 后， Q(zi) 就是后验概率，解决了 Q(zi) 如何选择的问题。这一步就是E步，建立 L(θ) 的下界。
接下来的M步，就是在给定 Q(zi) 后，调整 θ ，去极大化 L(θ) 的下界。那么一般的EM算法的步骤如下：

循环重复直到收敛 {
（E步）对于每一个 i ，计算

Q(zi)=p(zi|xi;θ)

（M步）计算

θ=argmaxθ∑i=1N∑ziQ(zi)logp(xi,zi;θ)Q(zi)

那么究竟怎么确保EM收敛？假定 θt 和 θt+1 是EM第 t 次和第 t+1 次迭代后的结果。如果 L(θt)≤L(θt+1) ，也就是说极大似然估计单调增加，且 L(θ) 有界，那么迭代会到达最大似然估计的最大值。下面证明 L(θt)≤L(θt+1) ：
固定 θt 后，E步

Qt(zi)=p(zi|xi;θt)

该步保证了在给定 θt 时，Jensen不等式中的等式成立，即

L(θt)=∑i=1N∑ziQt(zi)logp(xi,zi;θt)Qt(zi)

固定 Qt(zi) ，M步：
将 θt 视作变量，对 L(θt) 求导等于零可得到 θt+1 ，则下式成立：

L(θt)=∑i=1N∑ziQt(zi)logp(xi,zi;θt)Qt(zi)≤∑i=1N∑ziQt(zi)logp(xi,zi;θt+1)Qt(zi)≤∑i=1N∑ziQt+1(zi)logp(xi,zi;θt+1)Qt+1(zi)=L(θt+1)

证毕。
如果定义

J(Q,θ)=∑i=1N∑ziQ(zi)logp(xi,zi;θ)Q(zi),

则 J(Q,θ) 是 L(θ) 的下界。EM可以看作是 J 的坐标上升法，E步固定 θ ，优化 Q ，M步固定 Q 优化 θ 。

EM和GMM

给定训练样本 {xi}Ni=1 ，隐含类别标签用 zi 表示。与K-means硬指定不同，GMM认为 zi∈{1,2,...,K} 满足多项式分布 zi∼M(ϕ) ，其中 p(zi=j)=ϕj ， ϕj≥0 ， ∑Kj=1ϕj=1 。假定在给定 zi 的条件下 xi 满足多值高斯分布，即 (xi|zi=j)∼N(μj,σj) ，则联合分布 p(xi,zi)=p(xi|zi)p(zi) 。
GMM：

∑j=1KϕjN(μj,σj)

对于每个样例 xi ，先从 K 个类别中按多项式分布抽取一个 zi ，然后根据 zi 对应高斯分布生成样例 xi ，该过程称作混合高斯模型。注意： zi 是GMM的隐含随机变量， θ=(ϕ,μ,σ) 是GMM的参数，其中： ϕj 是样本类别中 zi=j 的比率， μj 是类别为 j 的样本特征均值， σj 是类别为 j 的样本特征方差。对数似然函数：

L(ϕ,μ,σ)=log∏i=1Np(xi;ϕ,μ,σ)=∑i=1Nlogp(xi;ϕ,μ,σ)=∑i=1Nlog∑zi=1Kp(xi,zi;ϕ,μ,σ)=∑i=1Nlog∑zi=1Kp(xi|zi;μ,σ)p(zi;ϕ)

该式不存在闭合解。考虑EM的思想，第一步是猜测隐含类别变量 ，第二步是更新其他参数，以获得最大的最大似然估计。
E步：固定 θ=(ϕj,μj,σj) ，求

wi(j)=Q(zi=j;θ)=p(zi=j|xi;θ)=p(xi,zi=j;θ)p(xi;θ)=p(xi|zi=j;μ,σ)p(zi=j;ϕ)∑Kl=1p(xi|zi=l;μ,σ)p(zi=l;ϕ)=12π√σjexp(−(xi−μj)22σ2j)⋅ϕj∑k=1K12π√σkexp(−(xi−μk)22σ2k)⋅ϕk

即每个样例 xi 的隐含类别 zi 为 j 的概率可以通过后验概率计算得到。对比K-means发现，每个样例分配的类别 zi 是有一定的概率的，每个样例 i 都要计算属于每一个类别 j 的概率。
M步：固定 wi(j) ，最大化

J(θ)=∑i=1N∑ziQ(zi)logp(xi,zi;θ)Q(zi)=∑i=1N∑j=1KQ(zi=j)logp(xi,zi;θ)Q(zi=j)=∑i=1N∑j=1Kwi(j)log12π√σjexp(−(xi−μj)22σ2j)⋅ϕjwi(j)

求参数 θ=(ϕj,μj,σj) 。
对 μj,σj 求导，得

∂J(θ)∂μj=∂∂μj⎛⎝∑i=1N∑j=1Kwi(j)⎡⎣log1wi(j)+log12π−−√σj−(xi−μj)22σ2j+logϕj⎤⎦⎞⎠=∑i=1Nwi(j)[1σ2j(μj−xi)μj]

∂J(θ)∂σj=∂∂σj⎛⎝∑i=1N∑j=1Kwi(j)⎡⎣log1wi(j)+log12π−−√+log1σj−(xi−μj)22σ2j+logϕj⎤⎦⎞⎠=∑i=1Nwi(j)[−1σj+1σ3j(xi−μj)2]

令其等于0，解得：

μj=∑Ni=1wi(j)xi∑Ni=1wi(j)σ2j=∑Ni=1wi(j)(xi−μj)2∑Ni=1wi(j)

同时，由于 ϕj≥0 ，且 ∑Kj=1ϕj=1 ，故建立拉格朗日函数

L(ϕj)=∑i=1Nwi(j)logϕj+β(∑Kj=1ϕj−1)

其中， ϕj 相关的常数被省略了。对 ϕj 求导等于0，结合 ∑Kj=1ϕj=1 可解得：

β=−∑i=1Nwi(j)ϕj=−∑j=1K∑i=1Nwi(j)∑j=1Kϕj=−∑i=1N∑j=1Kwi(j)=−∑i=1N1=−N

即：

ϕj=1N∑i=1Nwi(j)

算法过程如下：

循环下面步骤，直到收敛：{
（E步）对于每一个 i 和 j 计算

wi(j)=12π√σjexp(−(xi−μj)22σ2j)⋅ϕj∑k=1K12π√σkexp(−(xi−μk)22σ2k)⋅ϕk

（M步），更新参数：

ϕj=1N∑i=1Nwi(j)μj=∑Ni=1wi(j)xi∑Ni=1wi(j)σ2j=∑Ni=1wi(j)(xi−μj)2∑Ni=1wi(j)

}

E步中，将其他参数 ϕ,μ,σ 看作常量，计算 zi 的后验概率，也就是估计隐含类别变量。估计好后，利用上面的公式重新计算其他参数，计算好后发现最大化最大似然估计时， wi(j) 值又不对了，需要重新计算，周而复始，直至收敛。

GMM示例

给定由三个高斯的组成的混合模型（ K=3 ），其中：第一个高斯的均值 μ1=5 、方差 σ1=3 ，第二个高斯的均值 μ2=20 、方差 σ2=5 ，第三个高斯的均值 μ3=50 、方差 σ3=10 ，且三个高斯出现的概率为 ϕ1=0.2 、 ϕ1=0.4 、 ϕ1=0.4 。由该GMM生成10000个样本（ N=10000 ），并根据样本和给定的初始参数 ϕ=[0.33,0.33,0.34] 、 μ=[0,5,10] 、 σ=[5,5,5] ，迭代学习50次结果后收敛到 ϕ=[0.1969,0.4082,0.3950] 、 μ=[4.9686,20.0338,50.0925] 、 σ=[3.0639,5.0977,10.1096] 。下图给出了10000个样本的分布和50次迭代学习参数变化情况。

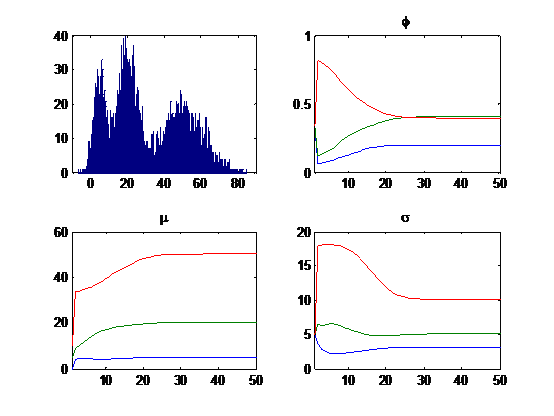
Matlab代码：

% 生成过程
phi1 = 0.2; mu1 = 5; sigma1 = 3;
phi2 = 0.4; mu2 = 20; sigma2 = 5;
phi3 = 0.4; mu3 = 50; sigma3 = 10;

N = 10000;
x = zeros(N,1);
for i = 1 : N
    rate = rand;
    if rate <= phi1
        x(i) = normrnd(mu1,sigma1);
    elseif rate <= phi1+phi2
        x(i) = normrnd(mu2,sigma2);
    else
        x(i) = normrnd(mu3,sigma3);
    end
end

figure(1); subplot(2,2,1); hist(x,1000);

% 学习过程
mu = [0, 5, 10];
sigma = [5, 5, 5];
phi = [0.33, 0.33, 0.34];
w = zeros(N,3);

T = 50;
mu_ = zeros(T+1,3);
sigma_ = zeros(T+1,3);
phi_ = zeros(T+1,3);
mu_(1,:) = mu;
sigma_(1,:) = sigma;
phi_(1,:) = phi;
for t = 1 : T
    % Expectation
    for k = 1 : 3
        w(:,k) = phi(k)*normpdf(x,mu(k),sigma(k));
    end
    w = w./repmat(sum(w,2),[1 3]);

    % Maximization
    for k = 1 : 3
        mu(k) = w(:,k)'*x / sum(w(:,k)); sigma(k) = sqrt(w(:,k)'*((x-mu(k)).*(x-mu(k))) / sum(w(:,k)));
        phi(k) = sum(w(:,k)) / N;
    end
    mu_(t+1,:) = mu;
    sigma_(t+1,:) = sigma;
    phi_(t+1,:) = phi;
end
figure(1); subplot(2,2,2); plot(phi_); title('\phi');
figure(1); subplot(2,2,3); plot(mu_); title('\mu');
figure(1); subplot(2,2,4); plot(sigma_); title('\sigma');