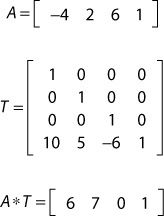第二章 A 3D/Math Primer
第二章 A 3D/Math Primer
本章介绍3D图形学的数学知识。借用一句Douglas Adams的名言,“别慌张”。我们会讲述vectors(向量),Matrix(矩阵),coordinate systems(坐标系统),transformations(变换),以及DirectXMath数学库。即使你已经很熟悉线性代数的知识,我也希望你能审核一下DirectX相关的内容。否则,做个深呼吸,坚持学习下去。
Vectors
你可能还记得高中物理课上学习的标量和向量的定义。标量是一个表示大小的量;向量是描述大小和方向的量。在3D图形学中Vectors有多种形式,可以表示速度,力量,方向或者简单的三维空间坐标点。
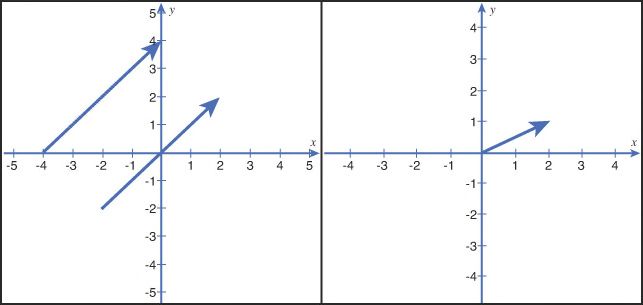
在几何数学中,可以把vector看作一个箭头;vector的长度即为大小,线段的指向即为vector的方向。在这种定义下,vector的尾部没有固定的位置。因此,判断两个vector相等只要比较他们的长度和方向是否都相等。但是,如果把vector的起点固定在坐标系统的原点,那么vector就可以表示成坐标系统中的一个点,该点指定了vector对应坐标轴的尺寸。在3D空间中,使用x,y,z坐标轴表示一个vector。比如点(2,5,8)表示一个距离原点对应于x轴偏移2个单位,y轴偏移5个单位,z轴偏移8个单位的vector。图2.1解释了2D中的情况。
图2.1 向量的表示。
Left-Handed and Right-Handed Coordinate Systems
图2.1显示了一个二维笛卡尔坐标系统(Cartesian coordinate system),x轴指向水平方向,y轴指向垂直方向,分别以向右和向上为正向。在三维空间中,z轴与x轴和y轴相互正交(垂直),根据左手或右手坐标系以指向屏幕里面或屏幕外面作为正向。在左手坐标系中,z轴朝向屏幕里面为正向,而在右手坐标系中朝向屏幕外面为正向。如何判断左右手坐标系有一个非常好的记忆方法,在你的眼前握住右手,保持拇指指向x轴的正向,食指指向y轴的正向,中指的指向即为z轴的正向也即朝向屏幕外面;左手刚好相反。图2.2描述了这两种坐标系。
图2.2 A mnemonic for 3D coordinate system hadedness。
Base Vector Operations
向量的加法和减法是两个向量各个部分都进行加减法,也就是两个向量中的各个元素对应的进行运算。例如,有两个向量a = (ax,ay,az)和b = (bx,by,bz),执行加法或减法产生向量c,依据表2.1执行这些操作。
表2.1 Basic Vector Operations
同理,乘法和除法是一个标量和一个向量的各个元素执行乘除法。下面是一个标量和向量相乘的例子:
4 * a = (4ax,4ay,4az)
Vector Length
vector的长度(或者大小)使用Pythagorean Theorem(勾股定理)进行计算。具体的使用以下公式(对于一个3维vector):
长度为1的vector称为unit vector(单位向量)。在只需要vector的方向而不用长度的情况下,unit vector是非常有用的。把一个vector的长度转变成1称为向量的标准化;标准化是通过把vector除以它的大小实现的。公式形式如下:
Dot Product(点积)
两个vectors的dot product是向量各个部分元素乘积的和。公式为:
a•b=(ax *bx)+(ay *by)+(az *bz)
这产生一个标量值,因些dot product也称为scalar product(或者inner product)。根据向量长度的定义,可以使用向量与其自身的点积的平方根来计算向量的长度。
在几何数学中,点积表示了两个向量之间的角度。公式为:
a • b = ||a||*||b|| * cos(θ)
θ即为向量a和b的夹角。如果向量a和b都已经标准化,点积可以简化为:
a • b = cos(θ)
根据这个公式,可以总结如下几点:
如果a • b > 0,两个向量的夹角小于90度。
如果a • b < 0,两个向量的夹角大于90度。
如果a • b = 0,两个向量相互垂直。
在后面的章节中,你会发现点积在计算机图形学中有多种多样的应用。比如,在光照计算中可以用点积来计算照射表面和光源之间的角度。在第二部分,“Shader Authoring with HLSL”将会详细讲解。
Cross Product(叉积)
Cross Product是另一个非常有用的向量运算。两个向量的叉积得到一个与这两个向量都正交的第三个向量。叉积的公式为:
a × b = (ay * bz – az * by, az * bx – ax * bz, ax * by – ay * bx)
叉积可以用于计算一个triangle的法向量(也就是triangle的朝向)。
a × b = (ay * bz – az * by, az * bx – ax * bz, ax * by – ay * bx)
叉积可以用于计算一个triangle的法向量(也就是triangle的朝向)。
Matrix
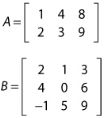
一个m×n矩阵是一个m行,n列的二维数组。比如一个4×1矩阵,有4行1列,一个2×3矩阵有两行3列,如下所示:
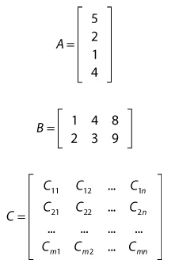
在矩阵C中,指出了矩阵中每个元素对应的下标。只有一个单一的行或列的矩阵有时被称为行向量和列向量。具有相同行数和列数的矩阵称为方阵。在3D图形学中,4×4方阵应用最广泛。

在矩阵C中,指出了矩阵中每个元素对应的下标。只有一个单一的行或列的矩阵有时被称为行向量和列向量。具有相同行数和列数的矩阵称为方阵。在3D图形学中,4×4方阵应用最广泛。
Basic Matrix Operations
你可以使用矩阵执行一些基本的算术运算。在向量中,是对两个向量的逐个元素执行加减法。因些两个矩阵必要具有相同的行数和列数才可以做加减法。标量乘法同样是进行逐个元素运算,把标量与矩阵中的每个元素相乘。但是,矩阵的乘法却有点不一样。
Matrix Multiplication
对于矩阵乘法,一个具有n列的矩阵只能和一个具有n行的矩阵相乘。在所得到的矩阵中,每一个元素都是第一个矩阵的行与第二个矩阵对应的列进行dot product计算出来的。如下公式所示,如果把矩阵A的每一行作为行向量,矩阵B的每一列作为列向量,可以定义乘积矩阵元素为:
图2.3 illustrates this process。
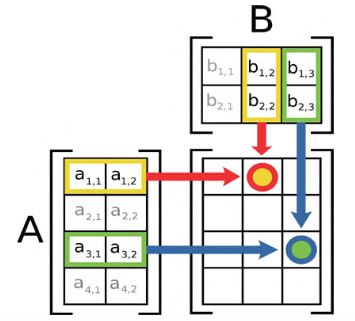
图2.3 Matrix multiplication。
图2.3 illustrates this process。

图2.3 Matrix multiplication。
如下所示:
矩阵A是一个两行3列的矩阵,矩阵B一个3行两列的矩阵。矩阵B的行数与A的列数相同,因此可以进行矩阵乘法。相乘的结果一个2×3矩阵,计算如下:
需要注意的是矩阵乘法是不满足交换律(不能交换相乘,也无法得到相同的乘积)。事实,一般情况下定义矩阵乘法A * B,对于B * A的情况是没有定义的,比如一个3×3矩阵乘以一个2×3矩阵。
需要注意的是矩阵乘法是不满足交换律(不能交换相乘,也无法得到相同的乘积)。事实,一般情况下定义矩阵乘法A * B,对于B * A的情况是没有定义的,比如一个3×3矩阵乘以一个2×3矩阵。
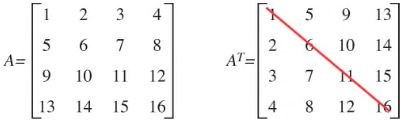
Transposition
Row-Major and Column-Major Order
处理矩阵时,必须考虑如何在计算机内存中存储矩阵。Direct3D以行优先的顺序存储矩阵,也就是说如果存储到一段连接内存中,是以一行一行的方式排列在内存中。这也是C语言中多维数组的存储格式。如下示例,是一个2×3矩阵以行优先顺序连接存储的形式:
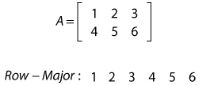
相反,同样的矩阵以列优先顺序存储在内存中的形式为:
Column − Major: 1 4 2 5 3 6
把一个行优先矩阵转成一个列优先矩阵涉及矩阵的转置(反之亦然)。如何存储矩阵会带来性能上的影响,而且不同的存储方法依赖于特定的顺序。将在第4章,“Hello,Shaders!”再讨论。
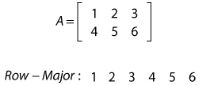
相反,同样的矩阵以列优先顺序存储在内存中的形式为:
Column − Major: 1 4 2 5 3 6
把一个行优先矩阵转成一个列优先矩阵涉及矩阵的转置(反之亦然)。如何存储矩阵会带来性能上的影响,而且不同的存储方法依赖于特定的顺序。将在第4章,“Hello,Shaders!”再讨论。
The Identity Matrix
单位矩阵是一个特殊的方阵,除了主对角线元素都是1之外,其他的元素都为0。例如一个4×4的单个矩阵定义为:
Transformations
前面已经讲过,vectors描述了3D空间中的方向和位置。比如,3D triangles中vertices的坐标位置就是用vectors存储的,两样法向量也是。但是在图形应用程序中vectors并不会一直保持不变。你的3D objects可能会在一个场景里移动,伸展,收缩,转动。专业的描述,位移称为translation(平移),伸展,收缩称为scaling(缩放),转动称为rotation(旋转)。这些操作统称为transformations(变换)。此外,想要把objects显示到屏幕上,需要经过多个参考坐标系的变换。矩阵将会用于把vectors的位置和方向从一个坐标系变换到另一个坐标系,同样用于translation,scaling和rotation。
Homogeneous Coordinates(齐次坐标)
在深入学习矩阵变换之前,需要特别注意的是我们将会使用齐次坐标。这种坐标系支持把translation,scaling,rotation操作合并到一个4×4矩阵。矩阵乘法满足结合律,因此可以把所有这些变换用一个4×4矩阵表示。在齐次坐标系中,每个坐标点有四个部分,分别为x,y,z,w。xyz坐标就是普通的3D坐标,坐标表示一个点的时候w为1,表示为方向的时候w为0。正如你所知道的,w = 0使得方向向量不能进行translation操作,这是非常有用的,因为单纯的方向向量在3D空间中是没有指明位置的。
Scaling
向量变换即执行向量-矩阵乘法,也就是一个矩阵乘以一个行向量或列向量。比如,3D缩放矩阵定义为:
主对角线上的数值表示对应于x,y,z轴的缩放因子。如果这些数据都相等,向量会等比例缩放。单位矩阵与此相似,相当于主对角线上数值都为1的缩放矩阵。
如下示例,使用一个非等比例的缩放矩阵变换一个点向量。点A的坐标为(-4,2,6,1)。其中第4列(w分量为1)是必须的,因为缩放矩阵有4列。
主对角线上的数值表示对应于x,y,z轴的缩放因子。如果这些数据都相等,向量会等比例缩放。单位矩阵与此相似,相当于主对角线上数值都为1的缩放矩阵。
如下示例,使用一个非等比例的缩放矩阵变换一个点向量。点A的坐标为(-4,2,6,1)。其中第4列(w分量为1)是必须的,因为缩放矩阵有4列。
Translation
Translation主要是沿着x,y,z轴移动object。平移矩阵定义如下:

以下示例描述了,一个点向量沿着x轴正向平移10个单位,沿y轴正向平移5个单位,没z的负向平移6个单位。如果向量的w分量为0(此时表示一个方向向量),那么平移变换没有任何效果。

以下示例描述了,一个点向量沿着x轴正向平移10个单位,沿y轴正向平移5个单位,没z的负向平移6个单位。如果向量的w分量为0(此时表示一个方向向量),那么平移变换没有任何效果。
Rotation
Rotation更复杂一点,因为每个坐标轴都对应一个不同的旋转矩阵。
以下示例描述了,把点(1,0,0)绕z轴逆时针方向旋转90度(π/2弧度)。
Matrix Concatenation(矩阵串联)
可以把多种变换矩阵串连成单个变换矩阵,而不是单独应用每一种变换。比如,缩放,旋转,平移矩阵可以组合成:
W = S * R * T
通过把缩放,旋转,平移串连成一个矩阵可以只需一步完成点向量变换。但是串连的顺序非常重要。矩阵串连是从左到右进行相乘,而且是不可交换的。例如,要渲染地球环绕太阳运行,地球相对太阳平移,还要绕着太阳旋转,那么串连矩阵也要按这种顺序执行。然而,如果还要模拟地球自转,那么在执行“公转”变换前要先执行自转的旋转操作。在这种情景下,完整的矩阵串连会是这样:
W = Raxial * T * Rorbit
只要明确从左到右要执行变换的顺序,那么可以串连任意数量的单个变换。
W = S * R * T
通过把缩放,旋转,平移串连成一个矩阵可以只需一步完成点向量变换。但是串连的顺序非常重要。矩阵串连是从左到右进行相乘,而且是不可交换的。例如,要渲染地球环绕太阳运行,地球相对太阳平移,还要绕着太阳旋转,那么串连矩阵也要按这种顺序执行。然而,如果还要模拟地球自转,那么在执行“公转”变换前要先执行自转的旋转操作。在这种情景下,完整的矩阵串连会是这样:
W = Raxial * T * Rorbit
只要明确从左到右要执行变换的顺序,那么可以串连任意数量的单个变换。
Changing Coordinates Systems
变换矩阵除了用于scaling,translation,rotation外,还可以用于把一个向量从一个坐标系转移到另一个坐标系。
Object Space and World Space
通常可以使用Autodesk Maya或者3D Studio Max等建模软件创建3D模型。模型本身所处的坐标系称为object space(或model space)。你的场景里可能包含成百上千个独立的模型,但是这些模型很少会作为一个整体去创建。而是分别存储在一个单独的文件中,而且它们的vertices只与模型的原点有关,与别的3D模型都没有关联。为了使用这些模型进行交互,必须共用一个通用的坐标系,也就是必须处于同一个世界中。因此,必须把这些模型从object space变换到world space。
World transformation matrix(世界坐标变换矩阵)由scale,translation,和rotation三个矩阵串联而成。只需要把3D模型的每个vertex与world matrix相乘就可以得到模型所处的world space。
View Space
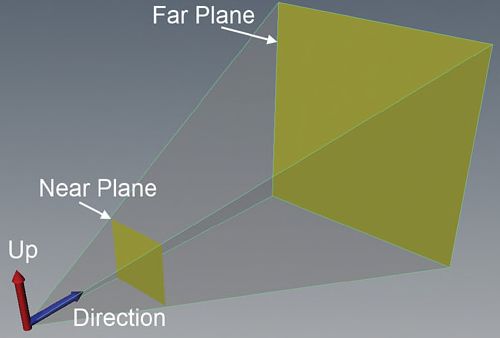
World space之后,object就变换到view space(或者camera space),这是一个相对于虚拟camera的坐标系。Camera的属性中定义了一个确定哪些object可见的空间体。这个空间体也被称为view frustum(视域体),如图2.4。View matrix用于把vectors从世界空间变换到视图空间,该矩阵由camera的位置(世界空间中),camera的朝向向量,以及一个表示朝向向上的向量组合计算得出的。在第三部分,“Rendering with DirectX”,将会讲角使用DirectX API创建view matrix。
图2.4 An illustration of the view frustum specified by the properties of a virtual camera.
Projection Space
Object space,world space和view space都是三维坐标系。但是,计算机屏幕却是二维的,projection matrix就是把3D几何图形投影到2D显示。在这个阶段,就可以描述深度的概念了,比如与屏幕越近的object比那些距屏幕较远的object看起来要大。这就是所谓的透视投影,与正交投影完全相反,正交投影的情况下所有object看起来与camera的距离都一样,不管实际的位置如何。
投影矩阵定义了视域体,并包含一个near plane(近裁剪面)和far plane(远裁剪面),一个垂直的视域,以及一个宽高比。在camera的和near plane之间的object是不可见的,超出far plane的object也不可见。就好比你的鼻子(near plane)和地平线(far plane)。视域定义了视域体的范围,宽高比即是显示器(或者窗口)的宽度除以高度。和view matrix一样,projection matrix也是调用DirectX API计算的。
World,view,projection space的变换都是在vertex shader阶段执行,但是需要你自己实现。可以单独使用每一种变换,也可以把这三个变换矩阵串联成一个world-view-projection矩阵,或者叫WVP。经过与投影矩阵相乘之后,所有的坐标都处于projection space(或者叫homogeneous clip space)中。