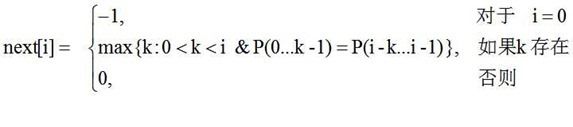经典算法题08-字符串模式匹配KMP
一. 提问
字符串模式匹配指的是,找出特定的字符串在一个较长的字符串中出现的位置。
有一个长字符串”ababcabababdc”,请问子串”babdc”出现的位置是哪里?
二. 思路
在字符串模式匹配的学习中,可能首先就会想起将模式字符串和目标字符串逐个去比较,直到匹配为止,这就BF(Brute Force)算法(称为“朴素”算法或者暴力算法),这算法的确可行,但是不高效。
BF(Brute Force)算法
基本思想是穷举法,即就是将目标串S的第一个字符与模式串P的第一个字符进行匹配,若相等,则继续比较S的第二个字符和P的第二个字符;若不相等,则比较S的第二个字符和P的第一个字符,依次比较下去,直到得出最后的匹配结果(如图所示)。

BF字符串模式匹配算法:
//wiki的BF
public static int BF(char S[], char T[], int pos) {//c从第pos位开始搜索匹配
int i = pos, j = 0;
while (S[i + j] != '.' && T[j] != '.') {
if (S[i + j] == T[j])
j++;
else {
i++;
j = 0;
}
}
if (T[j] == '.')
return i + 1;
else
return -1;
}
//自己写BF
public static int BFmath(String T, String P) {
int t = 0, p = 0;
int tLen = T.length();
int pLen = P.length();
if (tLen < pLen)
return -1;
while (p < pLen && t < tLen) {
if (T.charAt(t) == P.charAt(p)) {
p++;
t++;
} else {
t = t - p + 1;
p = 0;
}
}
if (p == pLen)
return t - pLen + 1;
else
return -1;
}朴素的模式匹配的算法复杂度是O( (n-m+1) * m) n为目标串的长度,m为模式串长度。
从其实现思想上可以很容易的看出,造成该算法低效的地方是在匹配不成功时主串和模式串的指针回溯上。
KMP算法
简单来讲KMP算法就是利用模式字符和匹配过程的已知条件得出一个值,去跳过在朴素算法逐个匹配过程中无必要的匹配,从而达到高效的算法。
为了避免指针的回溯,Knuth(D.E.Knuth)、Morris(J.H.Morris)和Pratt(V.R.Pratt)等人,发现其实每次右移的位数存在且与目标串无关,仅仅依赖模式本身,从而进行改进算法。
改进后的算法(简称为:KMP算法)的基本思想为:预先处理模式本身,分析其字符分布状况,并为模式中的每一个字符计算失配时应该右移的位数。这就是所谓的字符串的特征向量。
字符串的特征向量是KMP算法的关键,而这个字符串的特征向量也称为Next数组,所以如果我们可以得出这个Next数组就可以知道每一个字符失配时应该右移的位数。
这个所谓的Next数组(字符串的特征向量)怎么样可以求出?
“前缀子串”指除了最后一个字符以外,一个字符串的全部头部组合。
“后缀子串”指除了第一个字符以外,一个字符串的全部尾部组合。
定义”前缀子串”和”后缀子串”的最长的共有元素的长度为K值,称为特征数。
举一个栗子:
模式串:”ABCDABD”
“A”的前缀和后缀都为空集,共有元素的长度为0;
“AB”的前缀为[A],后缀为[B],共有元素的长度为0;
“ABC”的前缀为[A, AB],后缀为[BC, C],共有元素的长度0;
“ABCD”的前缀为[A, AB, ABC],后缀为[BCD, CD, D],共有元素的长度为0;
“ABCDA”的前缀为[A, AB, ABC, ABCD],后缀为[BCDA, CDA, DA, A],共有元素为”A”,长度为1;
“ABCDAB”的前缀为[A, AB, ABC, ABCD, ABCDA],后缀为[BCDAB, CDAB, DAB, AB, B],共有元素为”AB”,长度为2;
可知:所有的特征数组长度成为我们所求的Next数组(字符串的特征向量)。
由此可以得出模式P的特征向量Next的计算公式:
解释一下计算公式的使用:
next[j]来记录失配时模式串应该用哪一个字符于Si进行比较。
设 next[j]=k。根据公式我们有
next[j] = max{k | 0<k<j 且 P0P1..Pk-1=Pj-kPj-k+1...Pj-1}
-1 当j=0时 0 其他情况 好,接下来的问题就是如何求出next[j],这个也就是kmp思想的核心,对于next[j]的求法,我们采用递推法,现在我们知道了next[j]=k,我们来求next[j+1]=?的问题?其实也就是两种情况:
①:Pk=Pj 时 则P0P1…Pk=Pj-kPj-k+1…Pj, 则我们知:next[j+1]=k+1。
又因为next[j]=k,则: next[j+1]=next[j]+1。②:Pk!=Pj 时, 则P0P1…Pk!=Pj-kPj-k+1…Pj,
这种情况我们有点蛋疼,其实这里我们又将模式串的匹配问题转化为了上面我们提到的”主串“和”模式串“中寻找next的问题,你可以理解成在模式串的前缀串和后缀串中寻找next[j]的问题。现在我们的思路就是一定要找到这个k2,使得Pk2=Pj,然后将k2代入①就可以了。
设 k2=next[k]。 则有P0P1...Pk2-1=Pj-k2Pj-k2+1...Pj-1。 若 Pj=Pk2, 则 next[j+1]=k2+1=next[k]+1。 若 Pj!=Pk2, 则可以继续像上面递归的使用next,直到不存在k2为止。三. 编码
//计算字符串特征向量(优化版)
public static int[] getNext(String P) {
int i = 0;
int k = -1; //前缀串起始位置("-1"是方便计算)
int[] next = new int[P.length()]; // 动态存储区开辟整数数组
next[0] = -1;
while (i < P.length()-1) { //计算i=1...m-1的next值
if(k==-1 || P.charAt(k) == P.charAt(i)){
next[++i] = ++k; //pk=pi的情况: next[i+1]=k+1 => next[i+1]=next[i]+1
}else {
k = next[k]; //pk != pi 的情况:我们递推 k=next[k];要么找到,要么k=-1中止
}
}
return next;
}
//KMP模式匹配算法的实现
public static int KMPStrMatch(String T, String P) {
int[] next = getNext(P); //计算前缀串 和 后缀串的next
int t = 0,p = 0; //模式的下标变量
int pLen = P.length(); //模式的长度
int tLen = T.length(); //目标的长度
if (tLen < pLen) //如果目标比模式短,匹配无法成功
return -1;
while (p < pLen && t < tLen) { //反复比较对应字符来开始匹配
if (p == -1 || T.charAt(t) == P.charAt(p)) {
p++;
t++;
} else {
p = next[p];
}
}
if (p == pLen)
return t - pLen + 1;
else
return -1;
}附上jdk的实现方法:
String.indexOf(String)可见,也很经典的写法。
/**
* Code shared by String and StringBuffer to do searches. The
* source is the character array being searched, and the target
* is the string being searched for.
*
* @param source the characters being searched.
* @param sourceOffset offset of the source string.
* @param sourceCount count of the source string.
* @param target the characters being searched for.
* @param targetOffset offset of the target string.
* @param targetCount count of the target string.
* @param fromIndex the index to begin searching from.
*/
static int indexOf(char[] source, int sourceOffset, int sourceCount,
char[] target, int targetOffset, int targetCount,
int fromIndex) {
if (fromIndex >= sourceCount) {
return (targetCount == 0 ? sourceCount : -1);
}
if (fromIndex < 0) {
fromIndex = 0;
}
if (targetCount == 0) {
return fromIndex;
}
char first = target[targetOffset];
int max = sourceOffset + (sourceCount - targetCount);
for (int i = sourceOffset + fromIndex; i <= max; i++) {
/* Look for first character. */
if (source[i] != first) {
while (++i <= max && source[i] != first);
}
/* Found first character, now look at the rest of v2 */
if (i <= max) {
int j = i + 1;
int end = j + targetCount - 1;
for (int k = targetOffset + 1; j < end && source[j]
== target[k]; j++, k++);
if (j == end) {
/* Found whole string. */
return i - sourceOffset;
}
}
}
return -1;
}具体代码实现见我的github。
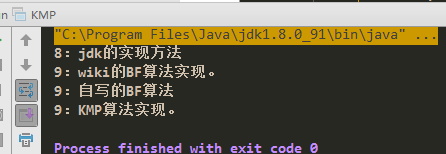
四. 结果:
五. 参考文献
极客学院wiki:http://wiki.jikexueyuan.com/project/kmp-algorithm/define.html
yahong:http://www.cnblogs.com/yahong/p/3420565.html