Stereo Matching文献笔记之（五）：经典算法DoubleBP读后感~

DoubleBP是一个立体匹配全局算法，来自于论文《Stereo Matching with Color-Weighted Correlation, Hierarchical Belief Propagation, and Occlusion Handling》，PAMI2009年提出，这是我第一篇读的，关于立体匹配方向的论文，当时感觉立体匹配太难了，很多概念都不知道是啥意思，比如说Color-Weighted Correlation，HBP，correlation volume，plane fitting，很庆幸，自己还是对能量函数的构造过程，建模过程比较清晰。当我完成立体匹配的项目之后，自己在回过头看这篇文章，很多地方理解的更加深刻了，在阅兵放假期间，就将我的理解写写~请大家不吝赐教哈~

这篇文章其实不难，还是秉承了PAMI的特点，都往框架方向构思，作者在序言部分说的很直白，DoubleBP共有两大贡献，一个是考虑到了图像的稳定点与非稳定点，然后根据低纹理区域和遮挡区域内的非稳定点来不断的更新能量函数中的数据项，最终使得视差能够正确地从稳定点传播到非稳定点（这点和tree filter那篇博客很像哦）。另一个就是融合了当前在立体匹配领域中几个不错的方法。所言不虚，因为在DoubleBP之前，所有的全局算法都没有考虑在稳定点上做文章，其实我们想想看，稳定点肯定靠谱一些，放弃不稳定点直觉上是正确的。

DoubleBP是绝对的全局算法，其重点放在了视差图的迭代求精上，靠的就是不断更新能量函数，然后利用HBP不断的求解。全局算法耗时严重，作者故意在设计算法的时候，使之更加适应并行计算。这样也具有一定的实际应用能力，但是很可惜，就算在FPGA上并行计算，仍旧达不到实时。

本文还是从算法思想，算法核心几个部分对DoubleBP进行描述。为了描述方便，我将代价计算值用CC值表示，将代价聚合值用CA来表示。

算法思想

DoubleBP似乎跳过了代价计算和代价聚合两个步骤，其实不然，其提出的correlation volume就是代价聚合的意思，计算correlation volume的相关公式如下所示：

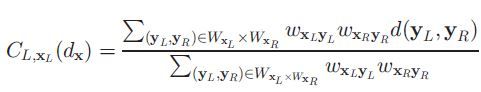
我为什么说这就是代价聚合？一般我们计算代价聚合的时候，先要基于左右两幅图像计算CC，然后往往只基于左图，基于每个目标像素周围的window来计算CA，首先要计算window内各个像素对目标像素的权值，权值乘以代价计算值再求和，就形成了目标像素的代价聚合值，这个公式也是如此，里面的d就是CC，唯一的区别在于权值的设计，这里面不仅考虑到了目标像素周围像素对它的权值，也考虑到了右图对应的目标像素周围像素的权值，二者采用连乘的方式。

之所以这样设计，是因为遮挡点边界两侧的颜色往往不同，颜色差距越大，对应的w就越小，correlation volume对遮挡像素就越不敏感。这里值得挑明的是，这个代价体其实就是对匹配代价所进行的双边滤波，权值同时考虑到了颜色和空间位置两大要素，具体原因请参考我的博客“《Spatial-Depth Super Resolution for Range Images》读后感~”，权值的计算公式如下所示：

代价聚合结束之后，往往直接采用WTA来计算视差图，本文也采用同样的方式。同时，它直接基于CA设计能量函数中的数据项，公式如下所示：

公式十分简单，就是一个对correlation volume的截断线性变换。之所以这么设计，是为了后续的HBP。但是，这个数据项的含义还是值得回味的，论文中说yita参数是correlation volume均值的两倍，为了防止图像中存在野值点，每个像素对应一个correlation volume，但是均值是多少个像素的均值？作者没说，我猜测是基于整幅图像。为什么这样可以防止野值点的干扰？我们想想看，如果图像中存在野值，那么左右两幅图像野值区域的像素correlation volume一定非常大（可以自己算算公式，也可以做个实验），如果我限制correlation volume的最大值，就可以间接的限制野值的干扰。

初始化的流程图直接引用作者的贴图

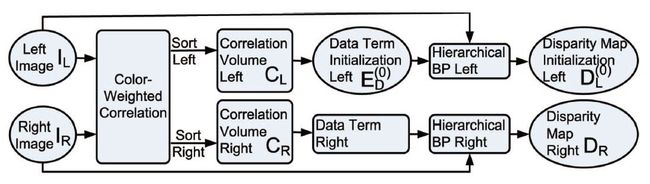
注意左右两幅图像均要计算出来各自的视差图，这种视差图效果很挫，有图为证。

这时，我们已经得到了左右两幅视差图，即将要进行的是mutual consistency check，其实就是左右图像一致性检查，对图像的像素进行分类，共分为遮挡点，稳定点和不稳定点三类。如果左视差图和右视差图得到的像素视差不等，那就说明它是遮挡点，否则进行一步细分，数学上的形式化公式如下所示：

这里值得重点说的是下面流程图中的稳定点和不稳定点的分类过程，作者为了达到这一目的，定义了一个叫做correlation confidence的距离度量方法，其实就是比较左右同一像素最好的两个correlation volume的改变程度，改变大就是稳定点，改变小就是不稳定点。

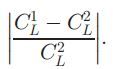
这部分一定感觉到很简单，但是意义却很大，只有将视差图的稳定点筛选出来，才能实现作者“将视差从稳定点扩散至不稳定点”的目标。流程图如下所示：

算法核心

这一节说一说这篇论文最精彩的部分，那就是对视差图的迭代求精，迭代求精是全局算法的终极手段，我们这个时候知道了视差图，知道了像素点的分类，当然还有原始图像，基于这三块内容，作者完成了一个漂亮的部分，其流程图如下所示：

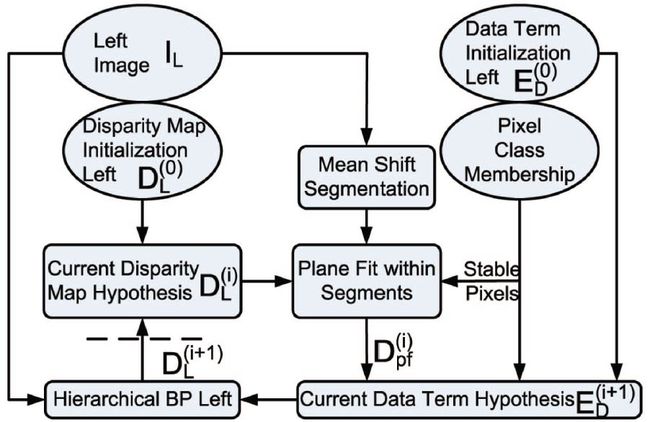
先说说算法整体的迭代流程，作者这个图画的很好，左下角部分，就是迭代循环，终止条件是虚线部分，这个迭代循环的输入值共有5个，分别是：图像分割结果，左图，左图视差图，像素分类结果（注意不是分割结果），以及上面说过的初始能量函数数据项。

plane fitting，我翻译成为平面拟合，对每一个分割区域都要进行，这里面有个拟合规则，如果该分割区域内稳定点的比例达到了70%，那么我们根据拟合结果确定非稳定点（遮挡点+不稳定点）的视差值，反之，连着稳定点一起算上，所有的像素点的视差值都要根据拟合结果来决定，拟合方法非常之多，多项式拟合，RANSAC等都可以。当然，稳定点越多，拟合出来的视差值误差肯定越小。

分割算法作者采用的是mean shift，其实这种分割算法不算好，可能是2009年文章的原因。

我们基于原始视差图Dl和稳定点计算出来新的视差图Dpf，下一步就要根据二者的差异来作为约束项，加上已有的数据项，用于根据不同的像素，构造新的数据项。注意，每个像素点都有一个数据项，这个时候还不是能量函数，只是数据项而已。

这个时候，本文最最晦涩难懂的一句话新鲜出炉了，就是下面这句话。。

从字面理解，它说的是这样的正则化项通过局部光滑限制的方式，保证了非稳定点始终与稳定点在同一平面，而这些稳定点已经与非稳定点在同一个分割区域中。

“老天爷啊！！这是啥啊？？？？”这就是我当初的状态。
后来冷静了许久，又回来品味这句话，自认为明白了作者的意思：每个分割区域内含有三类像素点，当我在进行平面拟合的时候，前提假设是他们都在一个plane上，这决定着得到的拟合视差图的质量高低，但是如何保证这个假设是一直成立的？答案是要通过数据项来保证，对非稳定点加以大的约束。这样，在每一步迭代中，就可以间接的保证同一分割区域内的非稳定点和稳定点始终都在一个平面内，这个时候用平面拟合才会靠谱，才会达到作者钟爱的，一直强调的“将视差从稳定点传播到非稳定点”的想法，game over。。。。。

关于HBP，置信度传播算法，是传统的解决马尔科夫图的优化方法，通过消息传递的机制来不断更新每个节点对应的权重，最终使得整个马尔科夫图像能量最小，HBP就是分层BP，也就是cross-scale那篇论文中提到的由粗到精的思想：将图像进行下采样，不同层次之间的像素存在对应关系，利用这种对应关系建立新的能量函数，其余的与BP一模一样。关于这块内容我要专门写一篇博客，因为它实在是太有用了。

结论

算法后续采用了“亚像素求精+均值滤波”的办法进一步提升了效果，我们会发现对于低纹理区域的黑色斑块，通过亚像素求精竟然全部消失，其实每个算法中都可以利用这种方法进行后处理，但是我在其他算法中得不到太明显的效果，远低于文本的提升，想来想去可能是由于经过迭代求精之后，DoubleBP得到的像素代价序列更加靠谱，这样求取的局部极值自然就更加精确，反之，如果求得的代价序列并不理想，那么经过二次多项式拟合之后，求取的极值可能会起到相反的作用。当然这只是我的实验效果的猜想，还请大家指教。

这是一篇很牛的文章，应该可以被称为全局立体匹配算法的代表性作品，用工程组合的方法，将多个模块组合起来，达到精确的估计效果，引用率很高，我看完这篇文章之后，最大的感觉就是在立体匹配这个领域，复杂的“一步到位”的方法，可能并不适用，还是工程组合的方法适合这个领域，这篇文章提出的像素分类，视差值从稳定点传递到不稳定点的思想，被多篇论文所采用，难怪作者认为这才是他最大的贡献。好文章，我说完了，不对的地方还请大家不吝指教哈！