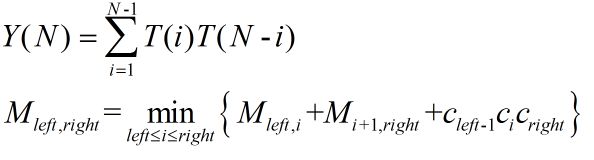算法设计技巧

从算法的实现向算法的设计转变，提供解决问题的思路

1.贪心算法

一种局部最优算法设计思路，思想是保证每一步选择在当前达到最优。一个很常见的贪心算法案例是零钱找取问题。

调度问题：书上的调度问题比较简单，其目标是所有作业的平均持续时间（调度+运行）最短，无论是但处理器还是多处理器，最优解的方案总是按作业的长短排序进行调度。《计算机算法设计与分析》上的作业调度的目标是最后完成时间最小，这要稍微复杂一些。

霍夫曼编码：最优编码必定保持满树的性质，基本问题在于找到总之最小的满二叉树。最简单的霍夫曼编码是一个两趟扫描算法：第一趟搜集频率数据，第二趟进行编码。

近似装箱问题：bin packing problem（不同于背包），分为两类：联机装箱（on-line packing）和脱机装箱（off-line packing），区别是脱机装箱具有先验性，而联机装箱不知道下一个到来的元素大小和总元素数目。

-- 可以证明，联机算法不能总给出最优解，也可以证明，存在一些输入使得任意联机装箱算法至少是最优箱子的4/3。有三种简单的算法可以保证最多使用两倍的最优装箱数。

1）丅项适配（next fit）：任意一个物品到来时，只检测当前箱子能否装下，线性时间运行。

2）首次适配（first fit）：依次扫描之前的箱子，寻找能放下当前物品的第一个箱子，O(N*N)运行（可以优化），可以证明，首次适配使用的箱子不多于1.7M（上取整）。

3）最佳适配（best fit）：将物品放到所有箱子中能够容纳它的最满的箱子中，不会超过1.7M。

-- 脱机算法：首次适配递减算法（fist fit decreasing），按照非增进行排序，然后进行fist fit装箱。

-- 应用：操作系统，在动态向堆申请内存的过程中，以隐式空闲链表实现的分配器放置分配的块时所采取的策略。（《深入理解计算机系统》修订版 P635）

2.分治算法

分治算法要求最优子结构 和独立(非重叠)子问题，算法通常由两部分组成divide-conquer。思路是递归解决较小的子问题，然后从子问题的解构建原问题的解。分治算法通常至少含有两个内部递归，其运行时间可通过下面的关系得到：

                                                    

                                                   

最近点问题：naive算法花费O(N*N)时间复杂度，可以将点空间划分为两半，递归的解两个子问题，然后进行合并。需要注意的是，合并的复杂度决定了最终的复杂度，所以要对合并的过程进行优化。思路是，首先取左右区域最小值的最小值dmin=min(dleft_min, dright_min)，作为中间区域的边界，横轴界为[middle-dmin, mindle+dmin]，纵轴自上而下以高度为dmin的窗口进行扫描，按照dmin的定义，窗口内待比较的元素不会超过7个，保证合并过程的线性复杂度，最终复杂度为O(NlogN)。算法执行前需进行O(NlogN)预处理，保留两个分别按照x坐标和y坐标排序的点的表P和Q。
选择问题：利用快排实现的选择问题可以在平均时间O(N)下进行，但其最坏复杂度为O(N*N)，即使是使用了三元素中值枢纽元，也不能提供避免最坏情况的保证。改进思路是从中项的样本中找出中项（五分化中项的中项，media-of-media-of-five partitioning）：将N个元素分成N/5（上取整）组，找出每组的中项，然后找出中项的中项作为枢纽元返回。可以证明：1）每个递归子问题的大小最多是原问题的70%，这样基本保证了快速选择的问题等分；2）用8次比较可以对5个数进行排序，然后递归的调用选择算法找出中项的中项，所以寻找枢纽元的复杂度为O(N)，最终的复杂度也为O(N)。

最后，五分化中项的中项方法系统开销太大，根本不实用。

整数相乘：不仅要进行子问题的划分，还要通过合并变换减少实际的乘法次数

矩阵相乘：同上。

3.动态规划

通常递归算法会重复一些子问题，造成不必要的性能下降。动态规划的思路是弃用递归，将子问题的答案系统的记录在中间表（table）中。其特点是最优子结构和重叠子问题。

矩阵连乘：寻找最优分割点。上式表示存在的组合数目，是一个指数形式，遍历开销太大；下式是对父问题的分解，注意Cleft-1。

                                 

算法实现：（数据大小很容易超出类型限制，注意比较边界）

#include "stdafx.h"
#include <iostream>
#include <vector>
#include "matrix.h" //自定义matrix类
using namespace std;

#define INFINITY 999999999

void optMatrix(const vector<int> &c, matrix<long> &m, matrix<long> &lastChange)
{
    //c[0]存储第一个矩阵的行数，剩下的分别存储第i个矩阵的列数
    int n = c.size() - 1;
    //将对角元素初始化为0，保护边界
    for(int i = 1; i <= n; i++)
        m.data[i][i] = 0;
    //k = right - left，left和right最大间隔是n-1
    for(int k = 1; k < n; k++)
        for(int left = 1; left <= n-k; left++)
        {
            int right = left + k;
            m.data[left][right] = INFINITY;
            for(int i = left; i < right; i++)
            {
                long currentCost = m.data[left][i] + m.data[i+1][right]
                    + c[left-1]*c[i]*c[right];
                if(currentCost < m.data[left][right])
                {
                    m.data[left][right] = currentCost;
                    lastChange.data[left][right] = i;
                }
            }
        }
}

最优二叉查找树：元素带权重（通常是出现的概率），目标是使得查找带来的开销最小，此时平衡二叉树不是最优。与矩阵连乘问题类似，子问题分解公式为：

                                     

所有点最短路径：Dijkstra算法对于单源最短路径查找为O(N*N)，所有点需要N次迭代。此处给出一种更紧凑的动态规划算法，该算法支持负值路径（Dijkstra不支持）。子问题分解式：

                                         

算法实现：

void dynamicDij(matrix<int> &a, matrix<int> &d, matrix<int> &route)
{
	//matrix<int> &a不能定义成const，否则调用不了getHeight()
	int n = a.getHeight();

	for(int i = 0; i < n; i++)
		for(int j = 0; j < n; j++)
		{
			d.data[i][j] = a.data[i][j];
			route.data[i][j] = -1;
		}

	for(int k = 0; k < n; k++)
		for(int i = 1; i < n; i++)
			for(int j = 0; j < n; j++)
			{
				int cost_tmp = d.data[i][k]+d.data[k][j];
				if(cost_tmp < d.data[i][j])
				{
					d.data[i][j] = cost_tmp;
					route.data[i][j] = k;
				}
			}	
}

4. 随机化算法

好的随机化算法没有不好的输入，而只有不好的随机数（考虑快排枢纽元的选取）。

随机数生成器：实现真正的随机数生成器是不可能的，依赖于算法，都是些伪随机数。产生随机数最简答的方法是线性同余生成器，Xi+1 = A Xi mod M，序列的最大生成周期为M-1，还需要仔细选择A，贸然修改通常意味着失败。需要注意的是，直接按照前面公式实现有可能发生溢出大数的现象，通常需要进行变换。

跳跃表：借助随机化算法实现以O(NlogN)期望时间支持查找和插入操作数据结构。本质是多指针链表。当查找时，从跳跃表节点的最高阶链开始寻找；当插入元素时，其阶数是随机的（抛硬币直到正面朝上时的总次数）。

素性测试：某些密码方案依赖于大数分解的难度。费马小定理（下1）：如果定理宣称一个数不是素数，那这个数肯定不是素数；若宣称是素数的话，有可能不是素数。可借助平方探测的特殊情况（下2）加以判断。

5.回溯算法

虽然分析回溯算法的复杂度可能很高，但实际上的性能却很好，明显优于穷举法。有时还会借助裁剪的方法进一步降低复杂度。与分支限界法不同，回溯算法通常是深度优先递归的搜索所有解，而分支限界通常是广度优先，找出满足条件的一个解。

公路收费问题：（重构问题远比创建问题复杂）一般以O(N*NlogN)运行（假设没有回溯，那么以优先队列实现d，每次插取数据logN，共插取了N*N次），最坏需花费指数时间。伪代码：

bool tuinpike(vector<int> &x, DisSet d, int n)
{
	x[1] = 0; //设置原点
	d.deleteMax(x[n]);
	d.deleteMax(x[n-1]);
	
	//由于问题在初始时具有对称性，因此判断一次即可
	if(x[n] - x[n-1] in d)
	{
		d.remove(x[n] - x[n-1]);
		return place(x, d, n, 2, n - 2);
	}
	else
		return false;
}

bool place(vector<int> &x, DisSet d, int n, int left, int right)
{
	bool found = false;

	if (d.isEmpty()) return ture;

	int max = d.findMax();

	if(|x[i] - max| in d, for all 1<=i<left, right<i<=n)
	{
		x[right] = max;
		for(1<=i<left, right<i<=n)
			d.remove(|x[i] - max|);
		found = place(x, d, n, left, right - 1);
		
		//backtrack不可行，恢复问题，换个方向继续试
		if(found == false)
		{
			for(1<=i<left, right<i<=n)
				d.insert(|x[i] - max|);
		}
	}

	if(found == false && |x[i] - (x[n] - max)| in d, for all 1<=i<left, right<i<=n )
	{
		x[left] = x[n] - max; //注意不是max
		for(1<=i<left, right<i<=n)
			d.remove(|x[i] - (x[n] - max)|);
		found = place(x, d, n, left + 1, right);

		if(found == false)
		{
			for(1<=i<left, right<i<=n)
				d.insert(|x[i] - (x[n] - max)|);
		}
	}

	return found;
}

博弈问题：待续

《数据结构与算法分析 C++描述》原书第10章整理