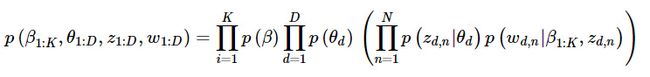LDA文档主题生成模型

基础知识：

LDA: latent dirichlet allocation ，又名潜在狄利克雷分布，是非监督机器学习技术，用于识别文档集中潜在的主题词信息。

主要思想：采用词袋方法，将每一篇文档视为词频向量，将文本信息转换为数字信息，没有考虑词与词之间的顺序。每一篇文档代表了一些主题所构成的概率分布，每一个主题又代表了很多单词所构成的概率分布。

文档主题生成模型：即三层贝叶斯概率模型，包含词、主题和文档。

生成模型：每个词通过“以一定的概率选择了主题，并从主题中以一定概率选择某个词语”的过程得到。

特点：文档到主题服从多项式分布，主题到词服从多项式分布

算法思想：

D:文档集合，T:主题集合，词袋：一篇文章中的单词,Vocabulary:所有文档中的词的集合

S1:统计D中每个文档d看作单词序列<w1,w2,...,wn>,wi表示第i个单词,设d有n个单词

S2:将D中涉及的所有单词组成Vocabulary,LDA以文档集合D作为输入，训练出两个结果向量(设聚成k个topic,Vocabulary中包含m个词):

S21:对每个D中的文档d,对应到不同主题的θd<pt1,pt2,...,ptk>,其中,pti表示d对应T中第i个主题的概率。pti=nti/n,nti是d中对应于T中第i个主题的词的数目，n是d中所有词的总数。

S22:对于T中每个主题topict,生成不同单词的概率φt<pw1,...,pwn>,pwi:表示t生成VOC中第i个单词的概率。pwi =Nwi/N,其中Nwi表示对应到主题的Vocabulary中第i个单词的数目,

N表示所有对应到topict的单词总数

核心公式:p(w|d) = p(w|t)*p(t|d)=θd * φt
,以主题词作为中间层

逻辑流程：

处理逻辑主要包含生成过程和学习过程

生成过程:

1为每一篇文档从主题分布中抽取一个主题

2从该主题对应的单词分布中抽取一个单词

3重复上述过程，直至遍历文档中每一个单词

记：文档到主题的分布为θ

记：主题到单词的分布为φ

学习过程：

方法总览：对于所有的文档和主题,随机给θd和φt赋值，不断重复上述过程，直到收敛，就是LDA的输出

1对于特定文档ds中第i个单词wi,若令该单词对应的topic为tj,把上述公式改写为

pj(wi|ds) = p(wi|tj) * p(tj|ds)

2枚举T中的topic,得到所有的pj(wi|ds),其中j的范围是[1,k]。根据概率值结果为ds中第i个单词wi选择一个topic.

最简单：令pj(wi|ds)最大的tj

3如果ds中第i个单词wi选择了与原先不同的主题，就对θd和φt有影响，反过来影响p(w|d)。对d中所有w进行一次p(w|d)的计算

并重新选择topic看作是一次迭代。进行n次迭代后，收敛到LDA的结果。

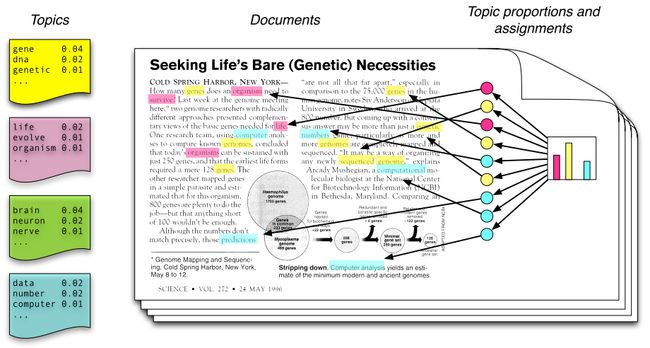
主题产生的过程:

是由词语的分布定义，比如蓝色主题是:2%概率的data,%2的number构成，....

一篇文章的产生过程:

文章是由一些主题构成。具体地，从主题集合中按概率分布选取一些主题，从主题中按概率分布选取一些词语，词语构成了最终的文档

我们的目标：计算这两个概率分布->得到模型，可以根据文档推断出它的主题分布，即分类。

文档->主题 是文档生成过程的逆过程

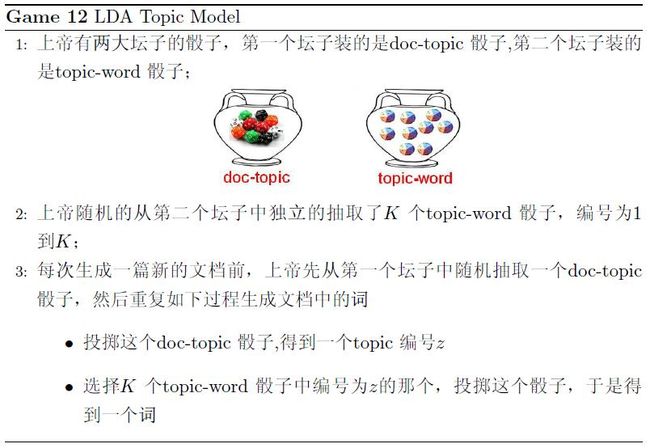
文档生成过程的描述:

1上帝有两个坛子的骰子，第一个坛子装的是文档到主题骰子，第二个坛子装的是主题到词语的骰子

2上帝从第二个坛子中独立抽取K个主题到词语骰子，编号为1~K

3每次生成一篇新的文档前，上帝从第一个坛子中随机抽取文档到主题的骰子，重复下列过程，生成文档中的词

   3.1 投掷这个文档到主题的骰子，得到主题编号z

    3.2选择K个主题到词的骰子中编号为z的那个，投掷这个骰子，得到一个词

概率模型：

LDA是使用联合分布来计算给定测量变量下隐藏变量的条件分布(后验分布)的

概率模型，观测变量为词的集合，隐藏变量为主题

联合分布：

参数解释:

β:主题

θ:主题概率

z:某个特定文档或词语的主题

w:单词

β_{1:K :主题集合}

_{βk :第k个主题的词的分布}

_{θd :第d个文档中该主题所占的比率}

_{θd,k :第d个文档中的第k个主题所占的比率}

_{zd :第d个文档的主题全体}

_{zd,n :第d个文档中第n个词所对应的主题}

_{wd :第d个文档的单词全体}

_{wd,n :第d个文档中第n个单词}

p(β）：从主题集合中选取特定主题的概率

p(θ_d)：该主题在特定文档中的概率

大括号里面前半部分：在主题确定的条件下，该文档第n个词的主题的概率

大括号里面后半部分：该文档第n个词的主题与该词的联合分布

连乘符号：随机变量的依赖性

词受两个方面影响：

1确定了主题后文档中该主题的分布θ_d

_{2第k个主题的词的分布βk}

后验分布：

分子：联合分布，给定语料库可计算

分母：无法暴力计算，文档集合词库达到百万

基于采样的算法通过收集后验分布样本，以样本的分布求得后验分布的近似。

θ_{d ：概率服从Dirichlet分布}

_{Zd,n:的分布服从多项式分布}

_{两个分布共轭，共轭：指先验分布和后验分布形式相同}