scikit-learn : 岭回归

背景

岭回归可以弥补线性回归的不足，它引入了正则化参数来”缩减”相关系数，可以理解为对相关系数做选择。当数据集中存在共线性的时候，岭回归就会有用。

让我们加载一个不满秩（low effective rank）数据集来比较岭回归和线性回归。秩是矩阵线性无关组的数量，满秩是指一个 m×n 矩阵中行向量或列向量中线性无关组的数量等于 min(m,n) 。

数据

构造模拟数据

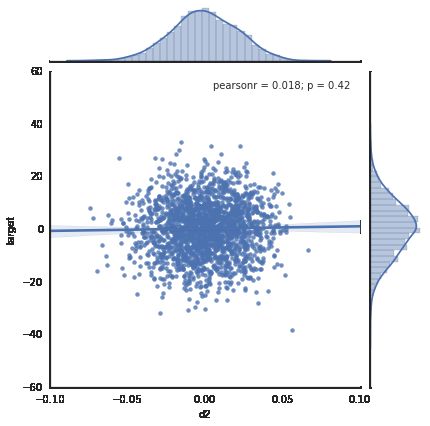
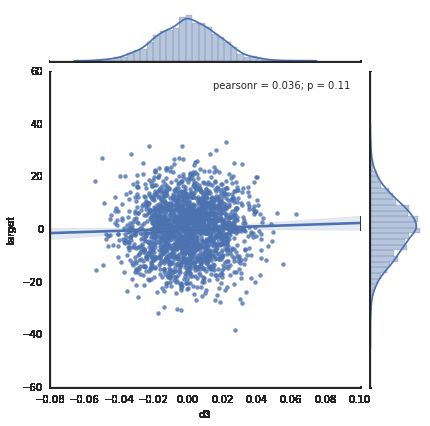
首先用make_regression建一个有3个自变量的数据集，但是其秩为2，因此3个自变量中有两个自变量存在相关性。

from sklearn.datasets import make_regression
reg_data, reg_target = make_regression(n_samples=2000, n_features=3, effective_rank=2, noise=10)

绘制散点图

import pandas as pd
import warnings # 用来忽略seaborn绘图库产生的warnings
warnings.filterwarnings("ignore")
import seaborn as sns
import matplotlib.pyplot as plt
sns.set(style="white", color_codes=True)
%matplotlib inline

def skdata2df(skSimuData,skSimuTarget):
    dfdata = pd.DataFrame(skSimuData,columns=["d1","d2","d3"])
    dfdata["target"] = skSimuTarget
    return dfdata
simuData = skdata2df(reg_data,reg_target)
fig = plt.figure()
for i,f in enumerate(["d1","d2","d3"]):
    sns.jointplot(x=f, y="target", data=simuData, kind='reg', size=6)

<matplotlib.figure.Figure at 0xcc23128>

普通的线性回归拟合模拟数据

import numpy as np
from sklearn.linear_model import LinearRegression
lr = LinearRegression()

def fit_2_regression(lr):
    n_bootstraps = 1000
    coefs = np.ones((n_bootstraps, 3))
    len_data = len(reg_data)
    subsample_size = np.int(0.75*len_data)
    subsample = lambda: np.random.choice(np.arange(0, len_data), size=subsample_size)

    for i in range(n_bootstraps):
        subsample_idx = subsample()
        subsample_X = reg_data[subsample_idx]
        subsample_y = reg_target[subsample_idx]
        lr.fit(subsample_X, subsample_y)
        coefs[i][0] = lr.coef_[0]
        coefs[i][1] = lr.coef_[1]
        coefs[i][2] = lr.coef_[2]
    %matplotlib inline
    import matplotlib.pyplot as plt
    f, axes = plt.subplots(nrows=3, sharey=True, sharex=True, figsize=(7, 5))
    f.tight_layout()

    for i, ax in enumerate(axes):
        ax.hist(coefs[:, i], color='b', alpha=.5)
        ax.set_title("Coef {}".format(i))
    return coefs

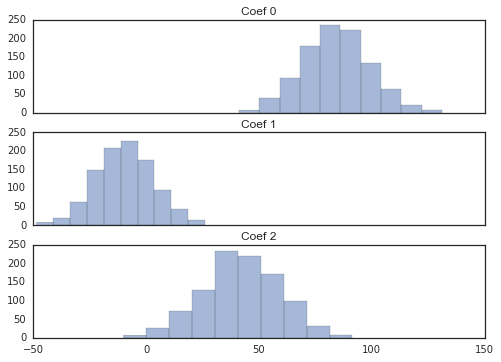
coefs = fit_2_regression(lr)

用岭回归（Ridge）拟合数据

from sklearn.linear_model import Ridge
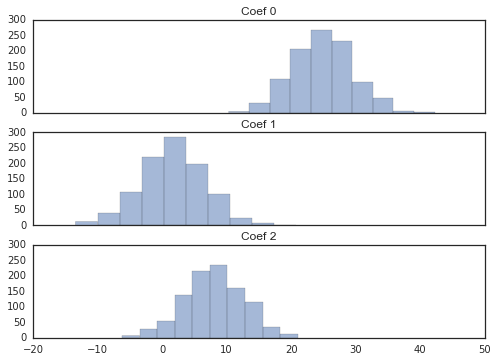
coefs_r = fit_2_regression(Ridge())

从上面两组图里可以看出，岭回归的相关系数更接近0。再看看两者相关系数的差异：

np.mean(coefs - coefs_r, axis=0)

array([ 59.37325536, -11.03784295,  34.01143862])

从均值上看，线性回归比岭回归的相关系数要大恨多。均值显示的差异其实是线性回归的相关系数隐含的偏差。那么，岭回归究竟有什么好处呢？让我们再看看相关系数的方差：

print "coefs_var:",np.var(coefs, axis=0)
print "coefs_r_var:",np.var(coefs_r, axis=0)

coefs_var: [ 215.46292923  162.3269464   276.29797874]
coefs_r_var: [ 21.56145591  24.13437546  21.4632597 ]

岭回归的相关系数方差也会小很多。这就是机器学习里著名的偏差-方差均衡(Bias-Variance Trade-off)。

方差和偏差一般来说，是从同一个数据集中，用科学的采样方法得到几个不同的子数据集，用这些子数据集得到的模型，就可以谈他们的方差和偏差的情况了。方差和偏差的变化一般是和模型的复杂程度成正比的，模型越复杂，偏差就越小，而模型越简单，偏差就越大。

岭回归与线性回归的不同

前面介绍过，线性回归的目标是最小化：

∥y^−Xβ∥2

岭回归的目标是最小化:

∥y^−Xβ∥2+∥ΓX∥2

其中， Γ 就是岭回归Ridge的alpha参数，指单位矩阵的倍数。

岭回归参数:

Ridge()

Ridge(alpha=1.0, copy_X=True, fit_intercept=True, max_iter=None,
   normalize=False, random_state=None, solver='auto', tol=0.001)

岭回归相关系数的解是：

β=(XT+ΓTΓ)−1Xy^

前面的一半和线性回归的相关系数的解是一样的，多了 ΓTΓ 一项。矩阵 A 的 AAT 的结果是对称矩阵，且是半正定矩阵(对任意非0向量 x ，有 xTAx≥0 )。相当于在线性回归的目标函数分母部分增加了一个很大的数。这样就把相关系数挤向0了。这样的解释比较粗糙，要深入了解，建议你看看SVD（矩阵奇异值分解）与岭回归的关系。