scikit-learn : 线性回归模型性能评估

背景

在这个主题中，我们将介绍回归模型拟合数据的效果。每当用线性模型拟合数据做完之后，我们应该问的第一个问题就是“拟合的效果如何？”本主题将回答这个问题。

线性模型

我们还用上一主题里的lr对象和boston数据集。lr对象已经拟合过数据，现在有许多方法可以用。

from sklearn import datasets
boston = datasets.load_boston()
from sklearn.linear_model import LinearRegression
lr = LinearRegression()
lr.fit(boston.data, boston.target)
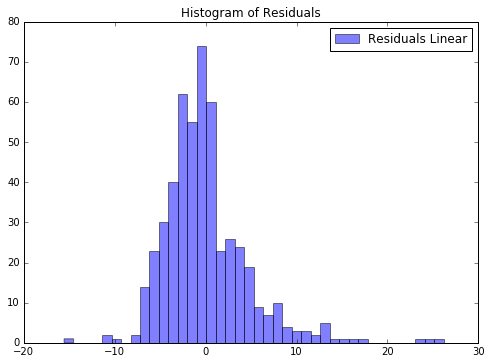
predictions = lr.predict(boston.data)

在线性回归那篇博客里，我们用残差直方图直观的展示拟合的效果。

%matplotlib inline
from matplotlib import pyplot as plt
f, ax = plt.subplots(figsize=(7, 5))
f.tight_layout()
ax.hist(boston.target - predictions,bins=40, label='Residuals Linear', color='b', alpha=.5);
ax.set_title("Histogram of Residuals")
ax.legend(loc='best');

计算残差的均值：

import numpy as np
np.mean(boston.target - predictions)

7.5828671405228079e-16

Q-Q图

另一个值得看的图是Q-Q图（分位数概率分布），我们用Scipy来实现图形，因为它内置这个概率分布图的方法：

Q-Q图是一种散点图,对应于正态分布的Q-Q图,就是由标准正态分布的分位数为横坐标,样本值为纵坐标的散点图. 要利用QQ图鉴别样本数据是否近似于正态分布,只需看QQ图上的点是否近似地在一条直线附近,而且该直线的斜率为标准差,截距为均值. 用QQ图还可获得样本偏度和峰度的粗略信息.

from scipy.stats import probplot
f = plt.figure(figsize=(8, 6))
ax = f.add_subplot(111)
probplot(boston.target - predictions, plot=ax);

均方误差 MAD(mean squared error)

这个图里面倾斜的数据比之前看的要更清楚一些。
我们还可以观察拟合其他量度，最常用的还有均方误差（mean squared error，MSE），平均绝对误差（mean absolute deviation，MAD）。让我们用Python实现这两个量度。后面我们用scikit-learn内置的量度来评估回归模型的效果：
MSE的计算公式是：

MAD=E(y¯t−yi)2

计算预测值与实际值的差，平方之后再求平均值。这其实就是我们寻找最佳相关系数时是目标。高斯－马尔可夫定理（Gauss-Markov theorem）实际上已经证明了线性回归的回归系数的最佳线性无偏估计（BLUE）就是最小均方误差的无偏估计（条件是误差变量不相关，0均值，同方差）。在用岭回归弥补线性回归的不足主题中，我们会看到，当我们的相关系数是有偏估计时会发生什么。

def MSE(target, predictions):
    squared_deviation = np.power(target - predictions, 2)
    return np.mean(squared_deviation)

print "MSE:",MSE(boston.target, predictions)

MSE: 21.8977792177

平均绝对误差 MAD(mean absolute deviation)

MAD是平均绝对误差，计算公式为：

MAD=|y¯t−yi|

线性回归的时候MAD通常不用，但是值得一看。为什么呢？可以看到每个量度的情况，还可以判断哪个量度更重要。例如，用MSE，较大的误差会获得更大的惩罚，因为平方把它放大。

def MAD(target, predictions):
    absolute_deviation = np.abs(target - predictions)
    return np.mean(absolute_deviation)

print "MAD:",MAD(boston.target, predictions)

MAD: 3.272944638

Boostrapping

还有一点需要说明，那就是相关系数是随机变量，因此它们是有分布的。让我们用bootstrapping（重复试验）来看看犯罪率的相关系数的分布情况。bootstrapping是一种学习参数估计不确定性的常用手段：

n_bootstraps = 1000
len_boston = len(boston.target)
subsample_size = np.int(0.5*len_boston)
subsample = lambda: np.random.choice(np.arange(0, len_boston),size=subsample_size)
coefs = np.ones(n_bootstraps)
for i in range(n_bootstraps):
    subsample_idx = subsample()
    subsample_X = boston.data[subsample_idx]
    subsample_y = boston.target[subsample_idx]
    lr.fit(subsample_X, subsample_y)
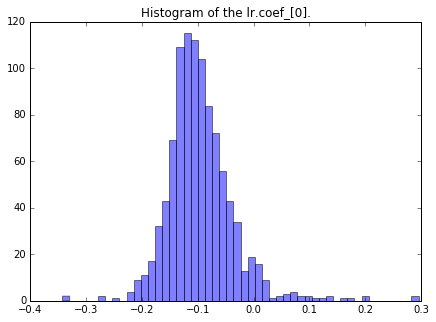
    coefs[i] = lr.coef_[0]#对应犯罪率相关系数

相关系数的分布直方图：

f = plt.figure(figsize=(7, 5))
ax = f.add_subplot(111)
ax.hist(coefs, bins=50, color='b', alpha=.5)
ax.set_title("Histogram of the lr.coef_[0].");

重复试验后的置信区间：

print "Confidence interval:",np.percentile(coefs, [2.5, 97.5])

Confidence interval: [-0.19127218  0.02423529]

置信区间的范围表面犯罪率其实不影响房价，因为0在置信区间里面，表面犯罪率可能与房价无关。
值得一提的是，bootstrapping可以获得更好的相关系数估计值，从上面相关系数的直方图可以看出使用bootstrapping方法的均值，会比普通估计方法更快地收敛（converge）到真实均值。