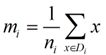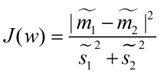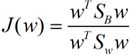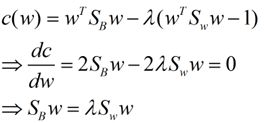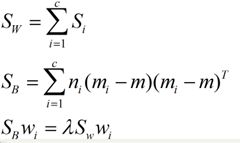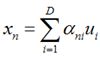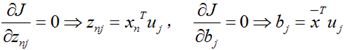chapter13 机器学习之利用PCA简化数据

LDA：

    LDA的全称是Linear Discriminant Analysis（线性判别分析），是一种supervised learning。有些资料上也称为是Fisher’s Linear Discriminant，因为它被Ronald Fisher发明自1936年，Discriminant这次词我个人的理解是，一个模型，不需要去通过概率的方法来训练、预测数据，比如说各种贝叶斯方法，就需要获取数据的先验、后验概率等等。LDA是在目前机器学习、数据挖掘领域经典且热门的一个算法，据我所知，百度的商务搜索部里面就用了不少这方面的算法。

    LDA的原理是，将带上标签的数据（点），通过投影的方法，投影到维度更低的空间中，使得投影后的点，会形成按类别区分，一簇一簇的情况，相同类别的点，将会在投影后的空间中更接近。要说明白LDA，首先得弄明白线性分类器(Linear Classifier)：因为LDA是一种线性分类器。对于K-分类的一个分类问题，会有K个线性函数：

     当满足条件：对于所有的j，都有Yk > Yj,的时候，我们就说x属于类别k。对于每一个分类，都有一个公式去算一个分值，在所有的公式得到的分值中，找一个最大的，就是所属的分类了。

    上式实际上就是一种投影，是将一个高维的点投影到一条高维的直线上，LDA最求的目标是，给出一个标注了类别的数据集，投影到了一条直线之后，能够使得点尽量的按类别区分开，当k=2即二分类问题的时候，如下图所示：

     红色的方形的点为0类的原始点、蓝色的方形点为1类的原始点，经过原点的那条线就是投影的直线，从图上可以清楚的看到，红色的点和蓝色的点被原点明显的分开了，这个数据只是随便画的，如果在高维的情况下，看起来会更好一点。下面我来推导一下二分类LDA问题的公式：

     假设用来区分二分类的直线（投影函数)为：

    LDA分类的一个目标是使得不同类别之间的距离越远越好，同一类别之中的距离越近越好，所以我们需要定义几个关键的值。

    类别i的原始中心点为：（Di表示属于类别i的点)

    类别i投影后的中心点为：

    衡量类别i投影后，类别点之间的分散程度（方差）为：

    最终我们可以得到一个下面的公式，表示LDA投影到w后的损失函数：

   我们分类的目标是，使得类别内的点距离越近越好（集中），类别间的点越远越好。分母表示每一个类别内的方差之和，方差越大表示一个类别内的点越分散，分子为两个类别各自的中心点的距离的平方，我们最大化J(w)就可以求出最优的w了。想要求出最优的w，可以使用拉格朗日乘子法，但是现在我们得到的J(w)里面，w是不能被单独提出来的，我们就得想办法将w单独提出来。

   我们定义一个投影前的各类别分散程度的矩阵，这个矩阵看起来有一点麻烦，其实意思是，如果某一个分类的输入点集Di里面的点距离这个分类的中心店mi越近，则Si里面元素的值就越小，如果分类的点都紧紧地围绕着mi，则Si里面的元素值越更接近0.

   带入Si，将J(w)分母化为：

   同样的将J(w)分子化为：

   这样损失函数可以化成下面的形式：

 

   这样就可以用最喜欢的拉格朗日乘子法了，但是还有一个问题，如果分子、分母是都可以取任意值的，那就会使得有无穷解，我们将分母限制为长度为1（这是用拉格朗日乘子法一个很重要的技巧，在下面将说的PCA里面也会用到，如果忘记了，请复习一下高数），并作为拉格朗日乘子法的限制条件，带入得到：

   这样的式子就是一个求特征值的问题了。

   对于N(N>2)分类的问题，我就直接写出下面的结论了：

   这同样是一个求特征值的问题，我们求出的第i大的特征向量，就是对应的Wi了。

   这里想多谈谈特征值，特征值在纯数学、量子力学、固体力学、计算机等等领域都有广泛的应用，特征值表示的是矩阵的性质，当我们取到矩阵的前N个最大的特征值的时候，我们可以说提取到的矩阵主要的成分（这个和之后的PCA相关，但是不是完全一样的概念）。在机器学习领域，不少的地方都要用到特征值的计算，比如说图像识别、pagerank、LDA、还有之后将会提到的PCA等等。

   下图是图像识别中广泛用到的特征脸（eigen face），提取出特征脸有两个目的，首先是为了压缩数据，对于一张图片，只需要保存其最重要的部分就是了，然后是为了使得程序更容易处理，在提取主要特征的时候，很多的噪声都被过滤掉了。跟下面将谈到的PCA的作用非常相关。

    特征值的求法有很多，求一个D * D的矩阵的时间复杂度是O(D^3), 也有一些求Top M的方法，比如说power method，它的时间复杂度是O(D^2 * M), 总体来说，求特征值是一个很费时间的操作，如果是单机环境下，是很局限的。

PCA：

    主成分分析（PCA）与LDA有着非常近似的意思，LDA的输入数据是带标签的，而PCA的输入数据是不带标签的，所以PCA是一种unsupervised learning。LDA通常来说是作为一个独立的算法存在，给定了训练数据后，将会得到一系列的判别函数（discriminate function），之后对于新的输入，就可以进行预测了。而PCA更像是一个预处理的方法，它可以将原本的数据降低维度，而使得降低了维度的数据之间的方差最大（也可以说投影误差最小，具体在之后的推导里面会谈到）。

    方差这个东西是个很有趣的，有些时候我们会考虑减少方差（比如说训练模型的时候，我们会考虑到方差-偏差的均衡），有的时候我们会尽量的增大方差。方差就像是一种信仰（强哥的话），不一定会有很严密的证明，从实践来说，通过尽量增大投影方差的PCA算法，确实可以提高我们的算法质量。

    说了这么多，推推公式可以帮助我们理解。我下面将用两种思路来推导出一个同样的表达式。首先是最大化投影后的方差，其次是最小化投影后的损失（投影产生的损失最小）。

    最大化方差法：

    假设我们还是将一个空间中的点投影到一个向量中去。首先，给出原空间的中心点：

    假设u1为投影向量，投影之后的方差为：

    上面这个式子如果看懂了之前推导LDA的过程，应该比较容易理解，如果线性代数里面的内容忘记了，可以再温习一下，优化上式等号右边的内容，还是用拉格朗日乘子法：

    将上式求导，使之为0，得到：

    这是一个标准的特征值表达式了，λ对应的特征值，u对应的特征向量。上式的左边取得最大值的条件就是λ1最大，也就是取得最大的特征值的时候。假设我们是要将一个D维的数据空间投影到M维的数据空间中（M < D)， 那我们取前M个特征向量构成的投影矩阵就是能够使得方差最大的矩阵了。

    最小化损失法：

    假设输入数据x是在D维空间中的点，那么，我们可以用D个正交的D维向量去完全的表示这个空间（这个空间中所有的向量都可以用这D个向量的线性组合得到）。在D维空间中，有无穷多种可能找这D个正交的D维向量，哪个组合是最合适的呢？

    假设我们已经找到了这D个向量，可以得到：

    我们可以用近似法来表示投影后的点：

    上式表示，得到的新的x是由前M 个基的线性组合加上后D - M个基的线性组合，注意这里的z是对于每个x都不同的，而b对于每个x是相同的，这样我们就可以用M个数来表示空间中的一个点，也就是使得数据降维了。但是这样降维后的数据，必然会产生一些扭曲，我们用J描述这种扭曲，我们的目标是，使得J最小：

    上式的意思很直观，就是对于每一个点，将降维后的点与原始的点之间的距离的平方和加起来，求平均值，我们就要使得这个平均值最小。我们令：

    将上面得到的z与b带入降维的表达式：

    将上式带入J的表达式得到：

     再用上拉普拉斯乘子法（此处略），可以得到，取得我们想要的投影基的表达式为：

    这里又是一个特征值的表达式，我们想要的前M个向量其实就是这里最大的M个特征值所对应的特征向量。证明这个还可以看看，我们J可以化为：

    也就是当误差J是由最小的D - M个特征值组成的时候，J取得最小值。跟上面的意思相同。

    下图是PCA的投影的一个表示，黑色的点是原始的点，带箭头的虚线是投影的向量，Pc1表示特征值最大的特征向量，pc2表示特征值次大的特征向量，两者是彼此正交的，因为这原本是一个2维的空间，所以最多有两个投影的向量，如果空间维度更高，则投影的向量会更多。

源码如下：

#coding=utf-8

'''
Created on Jun 1, 2011

@author: Peter Harrington

本章 按照数据方差最大方向调整数据的主成分分析降维方法。
chapter14、奇异值分解 它是矩阵分解技术中的一种，通过对原始数据的逼近来达到降维的目的。
chapter15、大数据下的机器学习


利用PAC简化数据

降维技术
主成分分析(PCA)
对半导体数据进行降维处理

在低维下，数据更容易进行处理，另外相关特性可能在数据中明确的显示出来，通常而言我们在应用其他机器学习算法之前们必须先识别出其相关特性

对数据进行简化具有如下好处
1、使得数据及更加容易使用
2、降低很多算法的计算开销
3、取出噪声
4、使得结果易懂



    第一种降维的方法称为主成分分析(Principal Component Analysis, PCA )。在PCA中，数据
从原来的坐标系转换到了新的坐标系，新坐标系的选择是由数据本身决定的。第一个新坐标轴选
择的是原始数据中方差最大的方向，第二个新坐标轴的选择和第一个坐标轴正交且具有最大方差
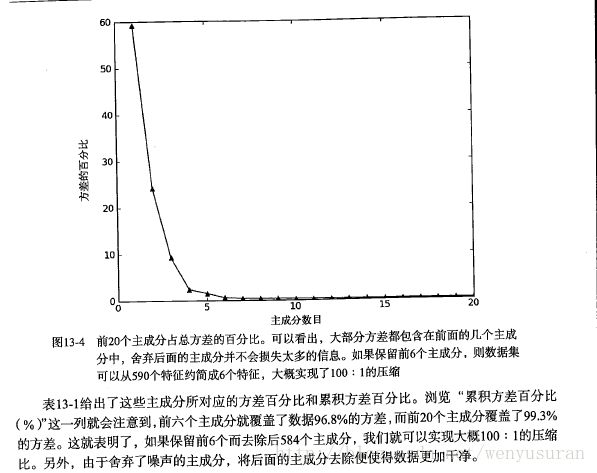
的方向。该过程一直重复，重复次数为原始数据中特征的数目。我们会发现，大部分方差都包含
在最前面的几个新坐标轴中。因此，我们可以忽略余下的坐标轴，即对数据进行了降维处理。在
13.2节我们将会对PCA的细节进行深人介绍。
    另外一种降维技术是因子分析(Factor Analysis )。在因子分析中，我们假设在观察数据的生
成中有一些观察不到的隐变量(latent variable )。假设观察数据是这些隐变量和某些噪声的线性
组合。那么隐变量的数据可能比观察数据的数目少，也就是说通过找到隐变量就可以实现数据的
降维。因子分析已经应用于社会科学、金融和其他领域中了。
    还有一种降维技术就是独立成分分析(Independent Component Analysis , ICA)。ICA假设数
据是从N个数据源生成的，这一点和因子分析有些类似。假设数据为多个数据源的混合观察结果，
这些数据源之间在统计上是相互独立的，而在PCA中只假设数据是不相关的。同因子分析一样，
如果数据源的数目少于观察数据的数目，则可以实现降维过程。


主成分分析：
优点:降低数据的复杂性，识别最重要的多个特征。
缺点:不一定需要，且可能损失有用信息。「
适用数据类型:数值型数据。

'''
from numpy import *


'''
在NumPy中实现PCA

将数据转换成前N个主成分的伪码大致如下:
去除平均值
计算协方差矩阵
计算协方差矩阵的特征值和特征向量
将特征值从大到小排序
保留最上面的N个特征向量
将数据转换到上述N个特征向量构建的新空间中

程序清单13
-1中的代码包含了通常的NwnPy导人和loadDataSet()函数。这里的load-
DataSet()函数和前面章节中的版本有所不同，
因为这里使用了两个list comprehension来构建矩阵。
pca()函数有两个参数:
第一个参数是用于进行PCA操作的数据集，第二个参数topNfeat
则是一个可选参数，即应用的N个特征。如果不指定topN
个特征，或者原始数据中全部的特征。
feat的值，那么函数就会返回前9 999 999
首先计算并减去原始数据集的平均值.。然后
计算协方差矩阵及其特征值，接着利用
根据特征值排序结果的逆序就可以得到
argsort()函数对特征值进行从小到大的排序。根据特征值}} l} } } a}7 } l} x}c p} }:} }} }o
topNfeat个最大的特征向量.。这些特征向量将构成后面对数据进行转换的矩阵，该矩阵则利
用N个特征将原始数据转换到新空间中.。最后，原始数据被重构后返回用于调试，同时降维之
后的数据集也被返回了。

'''
def loadDataSet(fileName, delim='\t'):
    fr = open(fileName)
    stringArr = [line.strip().split(delim) for line in fr.readlines()]   #使用两个list comprehension来构建矩阵。
    datArr = [map(float,line) for line in stringArr]
    return mat(datArr)

def pca(dataMat, topNfeat=9999999):
    meanVals = mean(dataMat, axis=0)
    meanRemoved = dataMat - meanVals #remove mean  计算并减去原始数据集的平均值
    covMat = cov(meanRemoved, rowvar=0)
    eigVals,eigVects = linalg.eig(mat(covMat))  #计算协方差矩阵及其特征值
    eigValInd = argsort(eigVals)            #sort, sort goes smallest to largest 对特征值进行从小到大的排序  根据特征值排序结果的逆序就可以得到topNfeat个最大的特征向量 从小到大对N值进行排序
    eigValInd = eigValInd[:-(topNfeat+1):-1]  #cut off unwanted dimensions  这些特征向量将构成后面对数据进行转换的矩阵，该矩阵则利用N个特征将原始数据转换到新空间中
    redEigVects = eigVects[:,eigValInd]       #reorganize eig vects largest to smallest
    lowDDataMat = meanRemoved * redEigVects#transform data into new dimensions
    reconMat = (lowDDataMat * redEigVects.T) + meanVals
    return lowDDataMat, reconMat  #最后原始数据被重构后返回用于测试，同时降维之后的数据集也被返回了
'''

def replaceNanWithMean(): 
    datMat = loadDataSet('secom.data', ' ')
    numFeat = shape(datMat)[1]
    for i in range(numFeat):
        meanVal = mean(datMat[nonzero(~isnan(datMat[:,i].A))[0],i]) #values that are not NaN (a number)
        datMat[nonzero(isnan(datMat[:,i].A))[0],i] = meanVal  #set NaN values to mean
    return datMat

>>> lowDMat,reconMat=pca.pca(dataMat,2)
>>> dataMat = pca.replaceNanWithMean()
>>> meanVals=mean(dataMat,axis=0)
>>> meanRemoved=dataMat-meanVals
>>> covMat = cov(meanRemoved,rowvar=0)
>>> eigVals,eigVects = linalg.eig(covMat)