老生常谈——哈希表
哈希表的概念
哈希表也叫做散列表,是一种根据关键码值(key value)来进行直接访问的数据结构。它通过某种映射关系,将关键码值映射到某个存储位置中来进行访问
用一个简单的公式描述为:存储位置=f(关键码值)
我们也将这种通过关键码值直接计算出存储位置的技术称之为散列技术。
散列技术本质上是用来描述记录的存储位置和记录的关键字之间的对应关系——也就是函数关系f。对弈任何一个关键词key对应一个存储位置f(key)。
这种对应关系f也就是所谓的映射关系,我们称之为映射函数,也叫散列函数,或者是哈希(Hash)函数。按照这个思路,利用散列技术将记录存储到一块连续的存储空间中,这块连续的存储空间称之为散列表或哈希表,关键字对应的记录的存储位置称之为散列地址。
哈希表的基本思想
哈希表(散列表)以表中的每个元素的关键字key为自变量,通过一定的函数关系f(key)计算出函数的值,把这个值作为数组的下标,将元素存入对应的数组中。
哈希表特性
1.存储:通过散列函数计算记录的散列地址,将记录存储到该散列地址。
2.查找:通过散列函数计算记录的散列地址,按照此地址访问该记录。
通过上面我们知道散列技术不但是一种存储方法也是一种查找方法。和以往的线性表、树、图等不同的是,这几种数据结构中的元素之间往往存在某种逻辑关系(一对一等),而散列技术的记录之间则不存在什么逻辑关系,它只和关键字有关。
因此,散列主要适用于面向查找的存储结构。但是以下几种情况不适用于哈希表:
- 大量不同记录中的关键字是一样的。比如说不同的学员信息,其性别只有男、女两种,如果用性别作为关键字,显然这不是一个很好的方案。
- 不适合于范围内查找。比如说将学员的年龄作为关键字,并希望查询18~30岁之间的学员信息,这显然是非常不合常理的。
除此之外,哈希表就是完美的么?显然不是!上面我们所谈的都是处在理想状态下——关键字不重复,其散列地址也重复。然而在现实世界中却会发生以下情况:
key1≠key2 ,但是 f(key1)=f(key2) ,我们将这种现象称之为冲突,并把 key1 和 key2 成为同义词。
哈希表查找的时间复杂度
由于哈希表存储的是键值对,查找时,是通过计算哈希码值来直接定位元素的存储位置,因为它不受元素数量影响,其时间复杂度为O(1)。
知道哈希表的特性可以让我们针对不同的情况学会高效的使用哈希表,但更重要的是学会如何设计一个简洁高效的哈希函数以及如何解决冲突。
哈希函数的设计
那么什么样的哈希函数才是优良的呢?一般来说,首先要计算简单,其次是要计算出的存储地址要均匀。计算简单保证了算法拥有较低的复杂度。计算出的存储地址均匀则保证整个存储空间是有效的,并在一定程度上减少为处理冲突而耗费的时间。值得我们注意的是,冲突是无法避免的。通常有如下几种设计哈希函数的方法:
1、直接定址法
2、除法取余法
3、数字分析法
4、平方取中法
5、折 叠 法
在这里为了更有明确性,我只选择其中常用的除法取余法来做简单的介绍。
对于哈希表长m的哈希函数而言,可表示为:
f(key)=keymodp(p⩽m)
此种方法的关键在于p的选择是否合理。如果不合理,则会产生大量的冲突。下面我们举例说明一下:
要存储的记录关键字集合为:{4,12,6,27,55,11,13,10}
如果设p为10,则存储情况如下:
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 关键字 | 10 | 11 | 12 | 13 | 4 | 55 | 6 | 27 | 8 |
我们发现这是一种很情况下几乎不会产生冲突。如果我们设p为6,发现:
4 mod 6=2;
12 mod 6=0;
6 mod 6=0;产生冲突
如果哈希表长为m,则p通常为小于或等于m的最小质数。
总之,应该根据现实况选择不同的哈希函数以及设定p。
处理哈希冲突
上面我们说到任何冲突无法完全避免,那一旦出现冲突之后应该如何处理呢?方案很多,打个比方说,你想租A栋709这件房子,结果你发先这间房子已经被被别人先租了,那应该怎么办呢?第一种是直接的方法就是看看能不能租A栋710;另一种方法是,如果这个房子里面是可以合租的,那我不就可以租房子中的一小间了么?第三种方法则是你会考虑B栋709能不能租呢?
这里的第一种方法类似开放地址法,而第二种方法就有点像链接法了,第三种方法就类似再散列的方法。
1、开放地址法
2、链接法
3、公共溢出区法
4、再散列的方法。
1、开发地址法
所谓的开发地址法也就是一旦发生冲突,则寻找下一个空的散列地址。如果散列表足够大,那么总可以找到一个空的散列地址。其公式如下:
fi(key)=(f(key)+di)modm(di=1,2,3,.....,m−1)
我们举个例子来说明一下:
要存储的记录关键字集合为:4、12、27、6、55、11,表长尾6
计算{4,12,27}时,不存在冲突情况,如下图所示:
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 |
| 关键字 | 12 | 4 | 27 |
当计算key=6时,f(6)=0,此时发现与12所在的位置冲突。这时用上面提到的公式
f(6)=f(f(6)+1) mod 6=1。这种做法就像A栋709被别人租了,那就尝试租A栋710此时如下图:
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 |
| 关键字 | 12 | 6 | 4 | 27 |
当计算key=55时,f(55)=1,此时发现与6所在的位置冲突,重复上述解决冲突的步骤:
f(55)=f(f(55)+1) mod 6=2,此时由于4所在的位置冲突,于是f(55)=f(f(55)+2) mod 6=3,仍然冲突,于是f(55)=f(f(55)+3) mod 6=4,此时存在空位,可直接存入,若下图所示:
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 |
| 关键字 | 12 | 6 | 4 | 27 | 55 |
当计算key=11时,f(11)=5,存在空位,直接存入,如下图所示:
| 下标 | 0 | 1 | 2 | 3 | 4 | 5 |
| 关键字 | 12 | 6 | 4 | 27 | 55 | 11 |
我们将以上这种——每次发生冲突之后,往下探测是否有空位置的的方法,称之为线性探测法。为了解决线性探测法只能从前往后寻找空位置这一缺点,出现了二次探测法。二次探测法的特点在于冲突发生时,在冲突的两侧进行跳跃式探测,直到找到空位置。其公式为:
fi(key)=(f(key)+di)modm(di=12,−12,22,−22,...,q2,−q2;q⩽m/2)
2、再散列的方法
在散列的方法就相当于在发现A栋709被租时,考虑B栋709,换句话说就是一旦发生冲突,则使用新的哈希函数重新计算一个存储地址,其公式为:
fi(key)=RHi(key)(i=1,2,....k)
这里RHi就是指的不同的散列函数。
3、链接法
开发寻址法和再散列方法所使用的哈希表结构是同一种(关键词对应的记录存放在数组当中),方法的本质就是一旦发生冲突就寻找下一个空散列地址。那么哈希表只有这一种结构么?
下面我们就来介绍另外一种由数组和链表共同组成的哈希表结构,其原理如下:
将所有哈希地址为i的元素构成一个称为同义词链的单链表,并将单链表的头指针存在哈希表的第i个单元
我们举个例子来说明一下:
要存储的记录关键字集合为:{4,12,27,6,55,11},表长为:6,哈希函数采用除法求余法。此时其哈希表结构如下图:
当关键字为6时,计算出的散列地址和12的散列地址冲突,此时直接将6接到12后即可。
我们可以看到这种特殊结构的哈希表有效的解决了冲突问题,绝对不会出现找不到存储地址的情况,但与之而来的是在查找过程中需要遍历单链表,此时将造成一定的性能损耗。
4、公共溢出区法
公共溢出区法则是一种更简单的处理冲突的方法,其理念就是分表存储——将哈希表分为基本表和溢出表两部分,凡是和基本表发生冲突的元素,一律填入溢出表。
同样,我们举例来说明一下:
要存储的记录关键字集合为:{4,12,27,6,55,11},表长为:6,哈希函数采用除法求余法。此时其哈希表结构如下图:
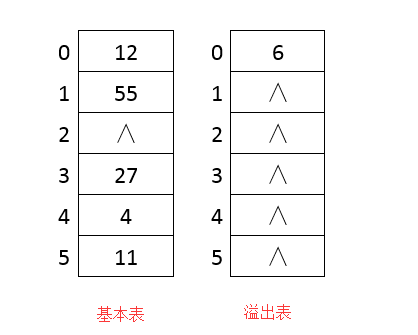
在查找时,对给定的关键词通过哈希函数计算出其散列地址,首先与基本表相应位置进行比对,如果相等,则代表查找成功;如果不相等,就到溢出表进行顺序查找。(注意:溢出表是顺序存储)
代码实现
上面我们简单的介绍一下哈希表的理论,但是理论只有化成实践才有效。下面我们通过代码来展示哈希表的构建和使用
#include<stdio.h>
#define HASH_LEN 13//哈希表长度
#define TABLE_LEN 8
int data[TABLE_LEN]={69,65,90,37,92,6,28,54};//待插入的原始数据
int hash[HASH_LEN]={0};//哈希表,初始化为0
void insertHash(int hash[],int m,int data)
{
int i;
i=data%HASH_LEN;//计算哈希地址
while(hash[i]){//元素位置已经被占用
i=(++i)%m;//采用线性探测法解决冲突
}
hash[i]=data;
}
void createHash(int hash[],int m,int data[],int n)
{
int i;
for(i=0;i<n;i++){
insertHash(hash,m,data[i]);
}
}
int searchHash(int hash[],int m,int key)
{
int i;
i=key%13;//计算哈希地址
while(hash[i]&&hash[i]!=key) {//判断是否冲突
i=(++i)%m;//线性探测法解决冲突
if(hash[i]==0){
return -1;//查找失败
}else{
return i;//查找成功
}
}
}
int main()
{
int key,i,pos;
createHash(hash,HASH_LEN,data,TABLE_LEN);//创建哈希表
printf("哈希表结构:");
for(i=0;i<HASH_LEN;i++)
printf("%ld,",hash[i]);
printf("\n");
printf("输入查找的关键词");
scanf("%ld",&key);
pos=searchHash(hash,HASH_LEN,key);
if(pos>0)
printf("查找成功); else printf("查找失败"); return 0; }