贪心算法-面试
基本思想
贪心算法(又称贪婪算法)是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,他所做出的是在某种意义上的局部最优解。
贪心算法不是对所有问题都能得到整体最优解,关键是贪心策略的选择,选择的贪心策略必须具备无后效性,即某个状态以前的过程不会影响以后的状态,只与当前状态有关。
面试题
分析
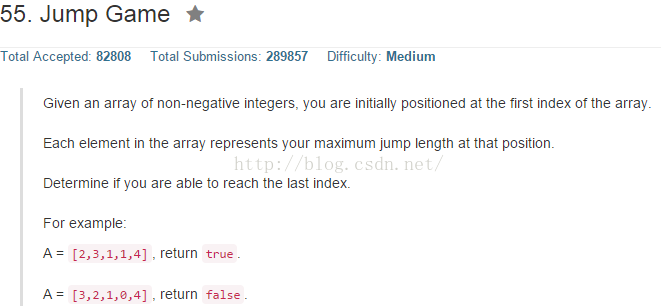
依次从当前的可达范围内搜寻下一步最大可达范围,注意避免重复搜索,只有新增的可达范围才可能发现新的最大可达范围。
public boolean canJump(int[] nums) {
int index=0,maxindex=index+nums[index];
while(index<=maxindex){
if(maxindex>=nums.length-1)
return true;
if(index+nums[index]>=maxindex)
maxindex=index+nums[index];
index++;
}
return false;
}
分析
同上,只是在搜索过程中记录步数。
public int jump(int[] nums) {
if(nums.length==1)return 0;
int start=1,step=1,end=nums[0];
while(end<nums.length-1){
step++;
int max=Integer.MIN_VALUE;
while(start<=end){
if(start+nums[start]>max)
max=start+nums[start];
start++;
}
end=max;
}
return step;
}
分析
最优选择:依次找到价格的最低点购入,然后找到价格最高点售出。
public int maxProfit(int[] prices) {
if(prices.length<=1) return 0;
int profit=0,minindex=0,maxindex;
while(true){
while(minindex+1<prices.length&&prices[minindex+1]<prices[minindex])
minindex++;
if(minindex==prices.length-1) break;
maxindex=minindex+1;
while(maxindex+1<prices.length&&prices[maxindex+1]>prices[maxindex])
maxindex++;
profit+=prices[maxindex]-prices[minindex];
if(maxindex==prices.length-1) break;
minindex=maxindex+1;
}
return profit;
}
分析
类似最长连续子段和。如果当前起点能继续行驶就继续往前行驶,不能行驶就更换起点。
public int canCompleteCircuit(int[] gas, int[] cost) {
if(gas.length==0)return-1;
int start=0,sum=0,end=0;
while(true){
sum+=gas[end]-cost[end];
if(sum<0){
if(end<start||end==gas.length-1)
return -1;
start=end+1;
end=start;
sum=0;
}else{
end=(end+1+gas.length)%gas.length;
if(end==start)
break;
}
}
return start;
}
分析
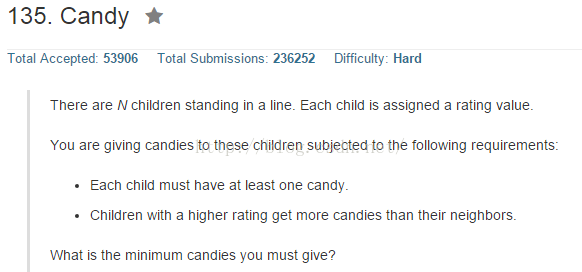
对于优先权递增的序列糖果数量递增,对于优先权递减的序列从最低点开始递增糖果数量,如果一个元素同时作为递增序列的结尾和递减序列的开始则取较大值。
我们可以将整个序列划分为多个波浪形(先增后减少)的序列,每个波谷的糖果数量都是1,波峰的数量取两侧的最大高度。例如一个波浪形优先权序列为1,3,7,6,5,4,2,分为两侧1,3,7和7,6,5,4,2,则糖果数量分别为1,2,5,4,3,2,1。对于优先权相等的情况,3,3,3,4这样的优先序列,分为三段波形3、3、3,4,这样糖果数量分别是1,1,1,2。
代码一
递归的方式求解,当递减序列过长时,递归深度过大会导致栈溢出,时间复杂度O(n),空间复杂度O(n)。
public int candy(int[] ratings) {
Map<Integer,Integer> candyMap=new HashMap<Integer,Integer>();
int sum=0;
for(int i=0;i<ratings.length;i++){
sum+=solve(ratings,i,candyMap);
}
return sum;
}
public int solve(int[] ratings,int index,Map<Integer,Integer> candyMap){
Integer count=candyMap.get(index);
if(count==null){
count=1;
//如果说
if(index>0&&ratings[index]>ratings[index-1]){
count=Math.max(count, solve(ratings,index-1,candyMap)+1);
}
if(index<ratings.length-1&&ratings[index]>ratings[index+1]){
count=Math.max(count, solve(ratings,index+1,candyMap)+1);
}
}
return count;
}
代码二
依次对每个波形进行处理,时间复杂度O(n),空间复杂度O(1)。
public int candy(int[] ratings) {
if(ratings.length<=1)return ratings.length;
int sum=0;
int start=0,max=0,end=0;
while(true){
max=start;
while(max+1<ratings.length&&ratings[max+1]>ratings[max])
max++;
end=max;
while(end+1<ratings.length&&ratings[end+1]<ratings[end])
end++;
int leftHight=max-start+1,rightHight=end-max+1;
sum+=Math.max(leftHight, rightHight);
for(int i=1;i<leftHight;i++)
sum+=i;
for(int i=1;i<rightHight;i++)
sum+=i;
if(end==ratings.length-1)
break;
if(ratings[end+1]==ratings[end]){
start=end+1;
}else{//波谷重合
sum-=1;
start=end;
}
}
return sum;
}
代码三
先从左往右扫描增序列,再从右往左扫描递减序列,时间复杂度O(n),空间复杂度O(1)。
public int candy(int[] ratings) {
int n=ratings.length;
int[] counts=new int[n];
for(int i=0;i<n;i++)counts[i]=1;
int sum=0;
for(int i=1,inc=1;i<n;i++){
if(ratings[i]>ratings[i-1])
counts[i]=Math.max(++inc,counts[i]);
else
inc=1;
}
for(int i=n-2,inc=1;i>=0;i--){
if(ratings[i]>ratings[i+1])
counts[i]=Math.max(++inc, counts[i]);
else
inc=1;
}
for(int i=0;i<n;i++)
sum+=counts[i];
return sum;
}