poj1240 Pre-Post-erous!

照例先上题目：

1:Pre-Post-erous!
查看 提交 统计 提问
总时间限制: 1000ms 内存限制: 65536kB
描述
We are all familiar with pre-order, in-order and post-order traversals of binary trees. A common problem in data structure classes is to find the pre-order traversal of a binary tree when given the in-order and post-order traversals. Alternatively, you can find the post-order traversal when given the in-order and pre-order. However, in general you cannot determine the in-order traversal of a tree when given its pre-order and post-order traversals. Consider the four binary trees below:

a a a a
/ / \ \
b b b b
/ \ / \
c c c c

All of these trees have the same pre-order and post-order traversals. This phenomenon is not restricted to binary trees, but holds for general m-ary trees as well.
输入
Input will consist of multiple problem instances. Each instance will consist of a line of the form
m s1 s2
indicating that the trees are m-ary trees, s1 is the pre-order traversal and s2 is the post-order traversal.All traversal strings will consist of lowercase alphabetic characters. For all input instances, 1 <= m <= 20 and the length of s1 and s2 will be between 1 and 26 inclusive. If the length of s1 is k (which is the same as the length of s2, of course), the first k letters of the alphabet will be used in the strings. An input line of 0 will terminate the input.
输出
For each problem instance, you should output one line containing the number of possible trees which would result in the pre-order and post-order traversals for the instance. All output values will be within the range of a 32-bit signed integer. For each problem instance, you are guaranteed that there is at least one tree with the given pre-order and post-order traversals.
样例输入
2 abc cba
2 abc bca
10 abc bca
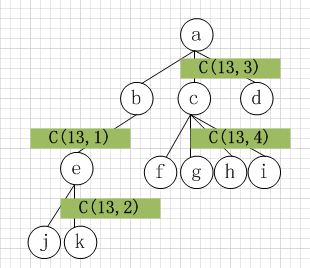
13 abejkcfghid jkebfghicda
0
样例输出
4
1
45
207352860
来源
East Central North America 2002

1. 在不作其他规定的情况下，对于一般的m叉树，dfs的方式仅有先根遍历和后根遍历。先根遍历和后根遍历都是递归定义的过程。
2. 先根遍历：访问根结点；然后按顺序先根遍历第0、1、2...m-1棵子树。后根遍历：按顺序后根遍历第0、1、2...m-1棵子树；然后访问根结点。

若给定m叉树的先根遍历和后根遍历序列，我们可以重建树的大致形状。举个例子，样例输入中的"13 abejkcfghid jkebfghicda":

最后得：

因此共计C(13, 3)*C(13, 1)*C(13, 4)*C(13, 2)=207352860种可能性。

代码清单：

#include <iostream>
#include <cstdio>
#include <string>
#include <cstring>
using namespace std;

#include <vector>

#define MAXLEN 30
char pre[MAXLEN];
char post[MAXLEN];

vector<int> branch_vec;

//计算n!
int factorial(int n)
{
	int result=1;

	if (n==0) return 1;
	else
	{
		for (int i=1; i<=n; ++i) result *= i;
		return result;
	}
}

//计算C(n, m)
int calc_C(int n, int m)
{
	unsigned int tmp=1;
	for (int i=0; i<m; ++i, --n) tmp*=n;

	return (tmp/(factorial(m)));
}

//计算每一个根结点有多少分支（子树）
void branch_count(int pr1, int pr2, int po1, int po2)	//参数是：preOrder序列的起止下标、postOrder序列的起止下标
{
	int a,b,len, branch=0;

	if(pr1==pr2 && po1==po2) return;	//递归出口：这个根结点没有任何子树。
	else
	{
		a=pr1+1;
		b=po1;
		len=0;

		while (b<po2)
		{
			while ( (pre[a] != post[b+len]) && (b+len<po2) ) ++len;
		
			++branch;	//每找到一个子树，++branch
			branch_count(a, a+len, b, b+len);	//对这个子树递归执行branch_count
		
			a=a+len+1;
			b=b+len+1;
			len=0;
		}

		branch_vec.push_back(branch);	//这个根结点的branch数目存入vector容器
	}
}

int main()
{
	freopen("D:\\in.txt", "r", stdin);  
	freopen("D:\\out.txt", "w", stdout); 

	int m, init_len, ans;

	while (1)
	{
		scanf("%d", &m);
		if(m==0) break;
		else
		{
			scanf("%s%s", pre, post);

			init_len=strlen(pre);

			branch_count(0, init_len-1, 0, init_len-1);

			ans=1;
			for (int i=0; i<branch_vec.size(); ++i)
			{
				ans*=(calc_C(m, branch_vec[i]));
			}

			printf("%d\n", ans);

			branch_vec.clear();
		}
	}

	return 0;
}