R实战之从头到尾分析广告数据集

前言

这篇文章主要用简单的线性回归模型来介绍统计学中一些很重要的概念。比如：置信区间（confidence interval）、t-statistic、p-value、 R2 statistic和F-statistic等一些概念。我会用具体的数据集来分析这些值分别意味着什么？并用具体的R代码来分析数据集并做出一个好的决策？

数据分析之前的几个重要问题

在提出问题之前，我先介绍一下Advertising数据集。数据集包含了200个不同市场的产品销售额，每个销售额对应3种广告媒体，分别是：TV, radio, 和 newspaper

如果我们能分析出广告媒体与销售额之间的关系，我们就可以更好地分配广告开支并且使销售额最大化。换句话说：我们的目标是开发出一个基于这3个广告媒体，准确预测销售额的模型。

下面，我提出几个问题，有着这些问题目标，我们的数据分析才有意义。

1. 广告预算与销售额之间存在关系吗？
2. 如果存在关系，它们之间的关系有多强？
3. 哪个媒体与销售额之间存在关系？
4. 每个媒体对销售额有多大的影响？
5. 我们对未来销售额的预测有多准确？

这篇文章中，我们假设线性模型是正确的，销售额之间是不存在协同关系的。在以后的文章中，我会写这些问题的。

估算线性回归系数并评估其准确性

为了清楚地解释一些统计学上的概念，在这里我只用最简单的线性回归，也就是只有一个变量的模型。定义如下模型：

sales^=β0^+β1^×TV^

在用R估算两个系数之前，我先给出residual sum of squares(RSS)的定义。如下：

RSS=(y1−β0^−β1^×x1)2+(y2−β0^−β1^×x2)2+⋯+(yn−β0^−β1^×xn)2

least squares方法就是选择出最好的 β0^和β1^ 来最小化RSS.下面我用具体的R代码来做这件事情。

adver <- read.csv("Advertising.csv",colClasses=c("NULL",NA,NA,NA,NA)) # 读取Advertising数据集,跳过第一列
fitadver=lm(Sales~TV,data=adver) # 用线性回归fit
coef(fitadver) # 查看估算出的系数
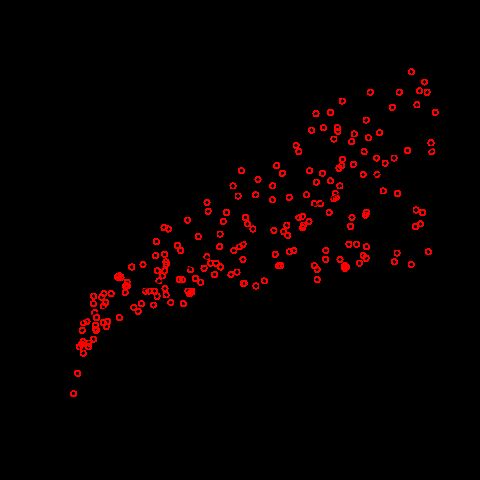
# plot数据点和已经估算出的线，图形如下
plot(adver$TV, adver$Sales, col="red", xlab='TV', ylab='sales')
abline(fit1)

PS：如果你想保存你的Plots作为图片，下面的代码就行，具体其它的格式请参考Saving Plots in R

dev.copy(png,'myplot.png')
dev.off()

为了更好地分析数据，下面给大家来点理论知识吧。哈哈！！！

上面我们已经估算出了相应的系数，可是这个系数有多么准确呢？为了更好地解释这个，我先举个例子。假设我们有一个随机变量Y，我们想找出它的平均值 μ ，但是我只知道它可能取到的一部分值 y1,y2,…,yn ， 因此这部分值的平均值是对 μ 很合理的一个估算。除非我们非常幸运，否则我们的这个估算值是不可能等于 μ 的，它要么比 μ 小，要么比 μ 大。但是，如果我们有很多这样的集合，我们就可以有很多的估算值，然后我们把这些值平均下来就会等于 μ 了。那么对 β0和β1 的估算是同样的道理。

我们已经知道把很多数据集上估算的值平均下来会很接近真正的 μ 值。但是，单个估算的值会与真正的 μ 值相差多少呢？为了回答这个问题，我们要求出 μ^ 的standard error.记作 SE(μ^) .这里有个非常有名的公式：

Var(μ^)=SE(μ^)2=σ2n

由上面的公式我们可以看出，其实求的就是 μ^ 的方差，即它离平均值（真正的 μ ）的距离。同样的道理， 对于 β0^和β1^ 也有相应的公式。

SE(β0^)2=σ2(1n+x¯2∑ni=1(xi−x¯)2)SE(β1^)2=σ2∑ni=1(xi−x¯)2

• 上面的 σ2=Var(ϵ)
• 为了使公式严格地成立，我们需要假设每个observation的误差 ϵi 是不相关的

通过上面求出的standard error，我们可以用它来计算confidence intervals.对于 β1 来说：我们有如下的confidence interval：

[β1^−2∗SE(β1^),β1^+2∗SE(β1^)]

大约有95%的机会真正的 β1 值包含在上面的区间中。对于 β0 也是同样的道理，我们也可以写出相似的confidence interval.下面，我用具体的R代码来求出上面 β1和β0 的confidence interval.

confint(fitadver)
# 输出结果如下
                 2.5 %     97.5 %
(Intercept) 6.12971927 7.93546783
TV          0.04223072 0.05284256

从上面的结果我们可以得出，对于 β0 来说：95%的confidence interval为[6.12971927，7.93546783];对于 β1 来说：95%的confidence interval为[0.04223072，0.05284256]。因此，我们可以得出结论：在没有广告的情况下，平均的销售额为6.12971927和7.93546783之间的某个值。在电视广告上我们每增加$1,000，增加的平均的销售额在42.23072和52.84256之间。

standard error也可以对系数执行hypothesis tests.最普遍的假设是null
hypothesis（ H0 ：在X和Y之间没有关系）和alternative hypothesis（ Ha ：在X和Y之间有关系）。数学上对应的是 H0：β1=0和Ha：β1≠0

为了判断上面的假设是否正确，下面我来介绍一下t-statistic和p-value这两个概念。为了拒绝null hypothesis我们需要判断 β1的估算β1^ 是够远离0的，因此我们可以很自信地说 β1 是非0的。但是，多远算是足够远呢？这取决于 SE(β1^) 。如果 SE(β1^) 是小的，那么即使是比较小的 β1^ 也有很强的证据表明 β1≠0 ，因此在X和Y之间存在关系。但是，如果 SE(β1^) 是大的，那么只有在绝对值 β1^ 很大的时候才能拒绝null hypothesis.在实际应用中，我们通常计算 β1^ 的t-statistic：

t=β1^−0SE(β1^)

上面的公式度量的实际是 β1^ 距离0的标准差。t越大证明它离0越远。在假设 β1=0 的情况下，p-value是可以观察到任何值大于等于|t|的概率。简单地说：在predictor和response之间没有关系的情况下，一个小的p-value表明你不可能在predictor和response之间观察到大的关联。因此，如果我们看到一个小的p-value就可以推断出在predictor和response之间存在关系。通常情况下，拒绝null hypothesis的p-value的切分点是5%或1%。当n=30，它们分别对应的t-statistic值大约为2和2.75

下面，我来用具体的R代码来打印上面模型系数的t-statistic和p-value

summary(fitadver)
# 输出结果如下
Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 7.032594   0.457843   15.36   <2e-16 ***
TV          0.047537   0.002691   17.67   <2e-16 ***

由于t-statistic的值为系数和其对应的standard error的比值，而 β0^和β1^ 相对于它们的standard error来说很大，所以它们的t-statistic也很大。那么 H0 成立的情况下，看到这么大的t-statistic值的概率几乎为0，大的t-statistic代表系数离0很远，因此 H0 不成立。我们现在可以得出结论为 β0≠0和β1≠0

评估模型的准确性

上面我们已经解释了估算出的系数的准确性，predictor和response之间是否有关系。下面，我们来解释一下估算出系数以后，整个模型的准备性到底怎么样？此时，你可能会想，只要我们的系数估算的准确，那模型正确率就是100%啊，但事实并非如此。其实我们的数据集来自的模型是这样的： Y=f(X)+ϵ ，即使你把所有的系数都求对，即 f(X) 求对，你的预测也不一定正确，因为误差项我们没法知道。

因此，我们要从现有的数据集中来评估模型的准确性。下面，我给出residual standard error(RSE)的定义：

RSE=1n−2RSS−−−−−−−−−−√=1n−2∑i=1n(yi−yi^)2−−−−−−−−−−−−−−−−√

实际上，RSE就是 ϵ 的标准差的估算。简单的说，它就是response
（预测值）偏离真正回归线的平均值。

回到我们上面的那个例子中，还是用summary那个R命令，我们就可以打印出求得的RSE为3.259。

如果预测值非常接近真实值，那么RSE将会很小，因此我们可以得出模型非常好在拟合了数据。然而，如果一个或多个observations的预测值和真实值相距很远，那么RSE会非常大，这表明模型并没有很好地拟合数据。

RSE是一种绝对的度量关于模型fit数据的不足。由于它的度量是以预测和真实值之间的绝对差异的形式进行的，因此什么样的RSE是一个好的RSE不总是清晰的。下面，我来介绍 R2 statistic，它的值始终在0与1之间，它相比RSE来说，具有更好地解释性。

R2=TSS−RSSTSS=1−RSSTSS

• TSS=∑(yi−y¯)2 ，叫做total sum of squares(TSS)

TSS测量的是关于response的总方差，可以把它当作是在线性回归执行前，内在变化性总量。而RSS测量的是在线性回归执行后，剩下未解释的变化性总量。因此，TSS − RSS测量的是通过执行线性回归，response中被解释的变化性总量。 R2 测量的是Y被X解释的变化性的比率。 R2 statistic接近于1表明response中大部分的变化性都被回归给解释了，而接近于0表明不没有解释太多的变化性，出现这样的情况可能是线性模型是错的，或者内部误差 σ2 很高。

在我们上面的例子中， R2 statistic是0.6119，因此TV只解释了sales中 23 的变化性。

多元线性回归

现在，我们已经知道了一些统计学的概念。下面，让我们来完善上面的模型吧。上面我用TV这一个predictor，现在我要用数据集中的所有predictors来构建模型。具体的R代码如下：

fitall=lm(Sales~.,data=adver)

在我们执行完多元线性回归后，你可能会感兴趣下面的几个问题。

一、至少有一个predictors对于预测response是有用的吗？

答：在只有一个predictor的时候，我们的 H0假设为β1=0 。那么现在假设我们有p个predictors，我们要把 H0的假设修改为β1=β2=⋯=βp=0 ,而 Ha为至少有一个βj≠0 。先前我们计算t-statistic，现在我们计算F-statistic，公式如下：

F=(TSS−RSS)/pRSS/(n−p−1)

如果 H0 为true，F-statistic的值接近于1;如果 Ha 为true，F-statistic将大于1.通过R中的summary命令，我们打印出上面模型的F-statistic值为570.3，远远大于1，这表明有很强的现象认为 H0 为false.也就是说，大的F-statistic表明至少有一个广告相关于sales.
然而，到底多大的F-statistic可以认为 H0 为false呢？答案是这取决于n和p的值。当n很大的时候，仅仅是比1大一点的F-statistic都可以认为 H0 为false;当n很小的时候，则需要一个更大的F-statistic. 前面t-statistic有一个对应的p-value,而对于F-statistic来说，同样有其对应的p-value,只要给定对应的n和p值，统计软件都会帮你计算出相应的p-value值。基于这个p-value,我们可以决定是否拒绝 H0
对于我们的数据集来说，F-statistic对应的p-value值非常接近于0，因此我们有强烈的迹象表明至少一个广告与sales是相关联的。

现在你可能会想，我们可以看每个系数对应的p-value，其中只要有一个值是非常小的，我们就可以说至少有一个predictor是相关于response的。为什么要费劲去计算F-statistic呢？这样的逻辑看似合理，实际上是不对的，尤其是当predictor的数量是非常大的时候。

假设我们有100个predictor，这100个predictor没有一个与response是相关的。但是，每一个predictor对应的p-value有5%的机会是小于0.05的。也就是说，对于100个predictor而言，我们有5个predictor对应的p-value是小的，即使在我们明知道这100个predictor没有一个与response是相关的情况下。因此，如果我们想要用单独的p-value去说明问题的话，那么会有很大的机率去总结一个错误的结论。而F-statistic没有这样的弊端，它是独立于predictor的数量的，即使在 H0 为true的情况下，它只有5%的概率p-value会很小，不论你有多少的predictor，这个概率都不会变。

二、哪一个predictor是重要的？

答：我们已经用F-statistic去表明至少有一个变量与response是有关联的。接下来我们会想，哪个变量是有关联的呢？这里我只列出几个经典方法的名字，有兴趣的可以去Google一下具体的做法，在以后的文章我会介绍更好的方法。
1、Forward selection
2、Backward selection
3、Mixed selection

三、模型拟合数据有多好？

答：我们还是看 R2和RSE 这两个量。
关于 R2 有一点应该注意：当更多的变量加入到模型中时，即使是这些变量与response有很弱地关联， R2 总是会增加。这是因为加变量使least squares方法更加准确地拟合training data（即使对testing data是没有必要的）， R2 也在training data被计算，因此它一定增加。
关于先前计算RSE的公式这里我也修正一下：

1n−p−1RSS−−−−−−−−−−−−−√

先前的公式只不过是当p=1时的特例

四、作出的预测有多么准确？

我们这里不讨论模型是否有偏差，也就是说我们认为线性模型是正确的。那么现在就只剩下两个应该考虑的问题。

1. 我们的预测值与真正的 f(X) 有多么接近？
2. 我们的预测值 Y^ 与真正的 Y 有多么接近？

在回答这两个问题之前，我先介绍一点知识。

通常情况下，真正Y与X之间的关系是： Y=f(X)+ϵ ,你可以把 f(X) 想象成我们要通过机器学习手段来学习到数据中潜在的模式，这个是reducible error，我们可以通过恰当的机器学习技术来减少我们的预测模型与它之间的误差。但是， ϵ 是irreducible error，这不是一个关于X的函数，因此你不能用X去预测它，在实际应用中我们也没法测量它，有很多因素会影响它的值，我们不去管它。我们真正关心的是要把reducible error做到最小。

如果你理解我上面说的，confidence interval度量的就是预测值与 f(X) 之间有多么接近。而prediction interval度量的是预测值与Y之间有多么接近。因此，prediction interval的区间范围要比confidence interval的区间范围要宽。

下面我用具体的R代码来演示一下：

new <- data.frame(TV=c(2,3,4),Radio=c(345,23,12), Newspaper=c(45,23,2)) # 我们想要预测的新数据

predict(fitall, new, interval="confidence") # 预测的结果以及相应的confidence interval
# 输出结果如下
        fit       lwr       upr
1 68.026587 62.584096 73.469078
2  7.388511  6.922937  7.854086
3  5.382233  4.838660  5.925806

predict(fitall, new, interval="prediction") # 预测的结果以及相应的prediction interval
# 输出结果如下
        fit       lwr       upr
1 68.026587 61.649275 74.403900
2  7.388511  4.032001 10.745022
3  5.382233  2.014018  8.750449

从上面的结果我们也可以看出prediction interval的区间范围要比confidence interval的区间范围要宽。

文章开篇问题答案

1题答案如下：

在多元线性回归那节，我们计算了F-statistic，它对应的p-value值很小，这表明广告预算与销售额之间存在关系。

2题答案如下：

R2 statistics大约为90%，也就是广告媒体解释了销售额90%的方差。这表明广告媒体与销售额之间存在很强的关系。

3题答案如下：

我们可以查看每个predictor对应的p-values值。在多元线性回归那节，TV和radio的p-values值是低的，而newspaper不是。这表明只有TV和radio与销售额之间存在关系。

4题答案如下：

我们看相应系数的置信区间就行了。

5题答案如下：

前面我已经解释过了，用prediction interval和confidence interval

结尾

有需要数据集的，留言给我，看到之后我发给你。