chapter2 机器学习之KNN(k-nearest neighbor algorithm)--K近邻算法从原理到实现

一.引入 

K近邻算法作为数据挖掘十大经典算法之一，其算法思想可谓是intuitive，就是从训练集里找离预测点最近的K个样本来预测分类

        因为算法思想简单，你可以用很多方法实现它，这时效率就是我们需要慎重考虑的事情，最简单的自然是求出测试样本和训练集所有点的距离然后排序选择前K个，这个是O(nlogn)的，而其实从N个数据找前K个数据是一个很常见的算法题，可以用最大堆(最小堆)实现，其效率是O（nlogk）的，而最广泛的算法是使用kd树来减少扫描的点，这也就是这篇文章的主要内容，本文偏实现，详细理论教程见july的文章 ，不得不服，july这篇文章巨细无遗！

二.前提：堆的实现

        堆是一种二叉树，用一个数组存储，对于k号元素，k*2号是其左儿子，k*2+1号是其右儿子

        而大根堆就是跟比左儿子和右儿子都大，小根堆反之。

        要满足这个条件我们需要通过up( index )操作和down( index )维护它的结构

        当然讲这个的文章实在有些多了，随便搜一篇大家看看：点击打开链接

        大小根堆的作用是

              a) 优先队列：因为第一个元素是最大或者最小的元素，所以可以实现优先队列

              b) 前K个最大(最小)值：这里限制堆的大小为k，来获得O( n log k)的效率，但注意此时小根堆是获得前K个最大值，大根堆是获得前K个最小值，插入的时候先把元素和堆顶比较再决定是否插入。

        因为事先KD-tree+BBF 要同时用到这两个东西，所以把它们实现在了同一个类里，感觉代码略漂亮，贴出来观赏一下：

        此代码是dml / tool / heap.py

  

from __future__ import division
import numpy as np
import scipy as sp
def heap_judge(a,b):
        return a>b

class Heap:
        def __init__(self,K=None,compare=heap_judge):
                '''''
                        'K'                 is the parameter to restrict the length of Heap
                                                !!! when K is confirmed,the Min heap contain Max K elements
                                                                  while Max heap contain Min K elements
                        'compare'         is the compare function which return a BOOL when pass two variable
                                                default is Max heap
                '''
                self.K=K
                self.compare=compare
                self.heap=['#']
                self.counter=0
        def insert(self,a):
                #print self.heap
                if self.K!=None:
                        print a.x,'==='
                if self.K==None:
                        self.heap.append(a)
                        self.counter+=1
                        self.up(self.counter)
                else:
                        if self.counter<self.K:
                                self.heap.append(a)
                                self.counter+=1
                                self.up(self.counter)
                        else:
                                if (not self.compare(a,self.heap[1])):
                                        self.heap[1]=a
                                        self.down(1)
                return
        def up(self,index):
                if (index==1):
                        return
                '''''
                print index
                for t in range(index+1):
                        if t==0:
                                continue
                        print self.heap[t].x
                print
                '''
                if self.compare(self.heap[index],self.heap[int(index/2)]):
                        #fit the condition
                        self.heap[index],self.heap[int(index/2)]=self.heap[int(index/2)],self.heap[index]
                        self.up(int(index/2))
                return
        def down(self,index):
                if 2*index>self.counter:
                        return
                tar_index=0
                if 2*index<self.counter:
                        if self.compare(self.heap[index*2],self.heap[index*2+1]):
                                tar_index=index*2
                        else:
                                tar_index=index*2+1
                else:
                        tar_index=index*2
                if not self.compare(self.heap[index],self.heap[tar_index]):
                        self.heap[index],self.heap[tar_index]=self.heap[tar_index],self.heap[index]
                        self.down(tar_index)
                return

        def delete(self,index):
                self.heap[index],self.heap[self.counter]=self.heap[self.counter],self.heap[index]
                self.heap.pop()
                self.counter-=1
                self.down(index)
                pass

        def delete_ele(self,a):
                try:
                        t=self.heap.index(a)
                except ValueError:
                        t=None
                if t!=None:
                        self.delete(t)
                return t

from __future__ import division
import numpy as np
import scipy as sp
def heap_judge(a,b):
        return a>b

class Heap:
        def __init__(self,K=None,compare=heap_judge):
                '''
                        'K'                 is the parameter to restrict the length of Heap
                                                !!! when K is confirmed,the Min heap contain Max K elements
                                                                  while Max heap contain Min K elements
                        'compare'         is the compare function which return a BOOL when pass two variable
                                                default is Max heap
                '''
                self.K=K
                self.compare=compare
                self.heap=['#']
                self.counter=0
        def insert(self,a):
                #print self.heap
                if self.K!=None:
                        print a.x,'==='
                if self.K==None:
                        self.heap.append(a)
                        self.counter+=1
                        self.up(self.counter)
                else:
                        if self.counter<self.K:
                                self.heap.append(a)
                                self.counter+=1
                                self.up(self.counter)
                        else:
                                if (not self.compare(a,self.heap[1])):
                                        self.heap[1]=a
                                        self.down(1)
                return
        def up(self,index):
                if (index==1):
                        return
                '''
                print index
                for t in range(index+1):
                        if t==0:
                                continue
                        print self.heap[t].x
                print 
                '''
                if self.compare(self.heap[index],self.heap[int(index/2)]):
                        #fit the condition
                        self.heap[index],self.heap[int(index/2)]=self.heap[int(index/2)],self.heap[index]
                        self.up(int(index/2))
                return
        def down(self,index):
                if 2*index>self.counter:
                        return
                tar_index=0
                if 2*index<self.counter:
                        if self.compare(self.heap[index*2],self.heap[index*2+1]):
                                tar_index=index*2
                        else:
                                tar_index=index*2+1
                else:
                        tar_index=index*2
                if not self.compare(self.heap[index],self.heap[tar_index]):
                        self.heap[index],self.heap[tar_index]=self.heap[tar_index],self.heap[index]
                        self.down(tar_index)
                return

        def delete(self,index):
                self.heap[index],self.heap[self.counter]=self.heap[self.counter],self.heap[index]
                self.heap.pop()
                self.counter-=1
                self.down(index)
                pass

        def delete_ele(self,a):
                try:
                        t=self.heap.index(a)
                except ValueError:
                        t=None
                if t!=None:
                        self.delete(t)
                return t

          传入的时候不设置K就是正常的优先队列，设置了K就是限制堆的大小了

          compare参数是比较大小的，默认是“数”的大根堆，你可以往堆里传任何类，只要有相适应的compare参数，比如我们KD-tree传的就是KD-Node

        

三.KD-BFF的原理：

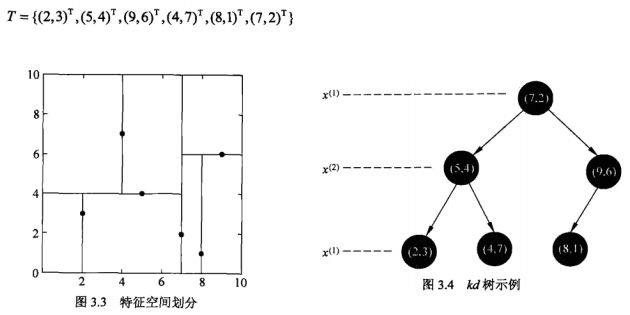
          首先从KD-Tree的创建说起：（直接贴《统计学习方法》的内容了）

         

          事实上从选择哪一个feature开始切割，还可以选择方差最大的那个参数，但是考虑到简便，以及我们可以选择更多的相似性度量方法，还是用《统计学习方法》里面的选择方式了。

          然后是KD-tree搜索的方法：（来自《统计学习方法》，但注意这里是最近邻，也就是k=1的时候）

         

          那么我们要K近邻要怎么做呢？就是用堆的第二个应用，用大根堆保持K个最小的距离，然后用根的距离(也就是其中最大的一个)来作为判断的依据是否有更近的点不在结果中，这一点很重要！

          同时摘录july博客的一段读者留言讲得非常好的：

              在某一层，分割面是第ki维，分割值是kv，那么 abs(q[ki]-kv) 就是没有选择的那个分支的优先级，也就是计算的是那一维上的距离； 同时，从优先队列里面取节点只在某次搜索到叶节点后才发生，计算过距离的节点不会出现在队列的，比如1~10这10个节点，你第一次搜索到叶节点的路径是1-5-7，那么1，5，7是不会出现在优先队列的。换句话说，优先队列里面存的都是查询路径上节点对应的相反子节点，比如：搜索左子树，就把对应这一层的右节点存进队列。

          大致这就是我们实现的基本思路了

四.KD-BFF的实现：

        知道原理了，并且有了堆这个工具之后我们就可以着手实现这个算法了：（终于要贴代码了）

       代码~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~此代码是 dml / KNN / kd.py

         

from __future__ import division
import numpy as np
import scipy as sp
from operator import itemgetter
from scipy.spatial.distance import euclidean
from dml.tool import Heap
class KDNode:
    def __init__(self,x,y,l):
        self.x=x
        self.y=y
        self.l=l
        self.F=None
        self.Lc=None
        self.Rc=None
        self.distsToNode=None

class KDTree:
    def __init__(self,X,y=None,dist=euclidean):
        self.X=X
        self.k=X.shape[0] #N
        self.y=y
        self.dist=dist
        self.P=self.maketree(X,y,0)
        self.P.F=None
    def maketree(self,data,y,deep):
        if data.size==0:
            return None
        lenght = data.shape[0]
        case = data.shape[1]
        p=int((case)/2)
        l = (deep%self.k)
        #print data
        data=np.vstack((data,y))
        data=np.array(sorted(data.transpose(),key=itemgetter(l))).transpose()
        #print data
        y=data[lenght,:]
        data=data[:lenght,:]

        v=data[l,p]
        rP=KDNode(data[:,p],y[p],l)
        #print data[:,p],y[p],l
        if case>1:
            ldata=data[:,data[l,:]<v]
            ly=y[data[l,:]<v]
            data[l,p]=v-1
            rdata=data[:,data[l,:]>=v]
            ry=y[data[l,:]>=v]
            data[l,p]=v
            rP.Lc=self.maketree(ldata,ly,deep+1)
            if rP.Lc!=None:
                rP.Lc.F=rP
            rP.Rc=self.maketree(rdata,ry,deep+1)
            if rP.Rc!=None:
                rP.Rc.F=rP
        return rP

    def search_knn(self,P,x,k,maxiter=200):
        def pf_compare(a,b):
            return self.dist(x,a.x)<self.dist(x,b.x)
        def ans_compare(a,b):
            return self.dist(x,a.x)>self.dist(x,b.x)
        pf_seq=Heap(compare=pf_compare)
        pf_seq.insert(P)    #prior sequence
        ans=Heap(k,compare=ans_compare)  #ans sequence
        while pf_seq.counter>0:
            t=pf_seq.heap[1]
            pf_seq.delete(1)
            flag=True
            if ans.counter==k:
                now=t.F
                #print ans.heap[1].x,'========'
                if now != None:
                    q=x.copy()
                    q[now.l]=now.x[now.l]
                    length=self.dist(q,x)
                    if length>self.dist(ans.heap[1].x,x):
                        flag=False
                    else:
                        flag=True
                else:
                    flag=True
            if flag:
                tp,pf_seq,ans=self.to_leaf(t,x,pf_seq,ans)
            #print "============="
            #ans.insert(tp)
        return ans


    def to_leaf(self,P,x,pf_seq,ans):
        tp=P
        if tp!=None:
            ans.insert(tp)
            if tp.x[tp.l]>x[tp.l]:
                if tp.Rc!=None:
                    pf_seq.insert(tp.Rc)
                if tp.Lc==None:
                    return tp,pf_seq,ans
                else:
                    return self.to_leaf(tp.Lc,x,pf_seq,ans)
            if tp.Lc!=None:
                pf_seq.insert(tp.Lc)
            if tp.Rc==None:
                    return tp,pf_seq,ans
            else:
                    return self.to_leaf(tp.Rc,x,pf_seq,ans)

from __future__ import division
import numpy as np
import scipy as sp
from operator import itemgetter
from scipy.spatial.distance import euclidean
from dml.tool import Heap
class KDNode:
	def __init__(self,x,y,l):
		self.x=x
		self.y=y
		self.l=l
		self.F=None
		self.Lc=None
		self.Rc=None
		self.distsToNode=None

class KDTree:
	def __init__(self,X,y=None,dist=euclidean):
		self.X=X
		self.k=X.shape[0] #N
		self.y=y
		self.dist=dist
		self.P=self.maketree(X,y,0)
		self.P.F=None
	def maketree(self,data,y,deep):
		if data.size==0:
			return None
		lenght = data.shape[0]
		case = data.shape[1]
		p=int((case)/2)
		l = (deep%self.k)
		#print data
		data=np.vstack((data,y))
		data=np.array(sorted(data.transpose(),key=itemgetter(l))).transpose()
		#print data
		y=data[lenght,:]
		data=data[:lenght,:]
		
		v=data[l,p]
		rP=KDNode(data[:,p],y[p],l)
		#print data[:,p],y[p],l
		if case>1:
			ldata=data[:,data[l,:]<v]
			ly=y[data[l,:]<v]
			data[l,p]=v-1
			rdata=data[:,data[l,:]>=v]
			ry=y[data[l,:]>=v]
			data[l,p]=v
			rP.Lc=self.maketree(ldata,ly,deep+1)
			if rP.Lc!=None:
				rP.Lc.F=rP
			rP.Rc=self.maketree(rdata,ry,deep+1)
			if rP.Rc!=None:
				rP.Rc.F=rP
		return rP

	def search_knn(self,P,x,k,maxiter=200):
		def pf_compare(a,b):
			return self.dist(x,a.x)<self.dist(x,b.x)
		def ans_compare(a,b):
			return self.dist(x,a.x)>self.dist(x,b.x)
		pf_seq=Heap(compare=pf_compare)
		pf_seq.insert(P)    #prior sequence
		ans=Heap(k,compare=ans_compare)  #ans sequence
		while pf_seq.counter>0:
			t=pf_seq.heap[1]
			pf_seq.delete(1)
			flag=True
			if ans.counter==k:
				now=t.F
				#print ans.heap[1].x,'========'
				if now != None:
					q=x.copy()
					q[now.l]=now.x[now.l]
					length=self.dist(q,x)
					if length>self.dist(ans.heap[1].x,x):
						flag=False
					else:
						flag=True
				else:
					flag=True
			if flag:
				tp,pf_seq,ans=self.to_leaf(t,x,pf_seq,ans)
			#print "============="
			#ans.insert(tp)
		return ans


	def to_leaf(self,P,x,pf_seq,ans):
		tp=P
		if tp!=None:
			ans.insert(tp)
			if tp.x[tp.l]>x[tp.l]:
				if tp.Rc!=None:
					pf_seq.insert(tp.Rc)
				if tp.Lc==None:
					return tp,pf_seq,ans
				else:
					return self.to_leaf(tp.Lc,x,pf_seq,ans)
			if tp.Lc!=None:
				pf_seq.insert(tp.Lc)
			if tp.Rc==None:
					return tp,pf_seq,ans
			else:
					return self.to_leaf(tp.Rc,x,pf_seq,ans)

       

        然后KNN就是对上面这个类的一个包装：

        代码~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~此代码是 dml / KNN / knn.py

    

#coding:utf-8
import numpy as np
import scipy as sp
from scipy.spatial.distance import cdist
from scipy.spatial.distance import euclidean
from dml.KNN.kd import KDTree

#import pylab as py
class KNNC:
    """docstring for KNNC"""
    def __init__(self,X,K,labels=None,dist=euclidean):
        '''''
            X is a N*M matrix where M is the case
            labels is prepare for the predict.
            dist is the similarity measurement way,

            The distance function can be ‘braycurtis’, ‘canberra’,
            ‘chebyshev’, ‘cityblock’, ‘correlation’, ‘cosine’,
            ‘dice’, ‘euclidean’, ‘hamming’, ‘jaccard’, ‘kulsinski’,
            ‘mahalanobis’,

        '''
        self.X = np.array(X)
        if labels==None:
            np.zeros((1,self.X.shape[1]))
        self.labels = np.array(labels)
        self.K = K
        self.dist = dist
        self.KDTrees=KDTree(X,labels,self.dist)

    def predict(self,x,k):
        ans=self.KDTrees.search_knn(self.KDTrees.P,x,k)
        dc={}
        maxx=0
        y=0
        for i in range(ans.counter+1):
            if i==0:
                continue
            dc.setdefault(ans.heap[i].y,0)
            dc[ans.heap[i].y]+=1
            if dc[ans.heap[i].y]>maxx:
                maxx=dc[ans.heap[i].y]
                y=ans.heap[i].y
        return y
    def pred(self,test_x,k=None):
        '''''
            test_x is a N*TM matrix,and indicate TM test case
            you can redecide the k
        '''
        if k==None:
            k=self.K
        test_case=np.array(test_x)
        y=[]
        for i in range(test_case.shape[1]):
            y.append(self.predict(test_case[:,i].transpose(),k))
        return y

#coding:utf-8 
import numpy as np
import scipy as sp
from scipy.spatial.distance import cdist
from scipy.spatial.distance import euclidean
from dml.KNN.kd import KDTree

#import pylab as py
class KNNC:
	"""docstring for KNNC"""
	def __init__(self,X,K,labels=None,dist=euclidean):
		'''
			X is a N*M matrix where M is the case 
			labels is prepare for the predict.
			dist is the similarity measurement way,

			The distance function can be ‘braycurtis’, ‘canberra’, 
			‘chebyshev’, ‘cityblock’, ‘correlation’, ‘cosine’, 
			‘dice’, ‘euclidean’, ‘hamming’, ‘jaccard’, ‘kulsinski’, 
			‘mahalanobis’, 

		'''
		self.X = np.array(X)
		if labels==None:
			np.zeros((1,self.X.shape[1]))
		self.labels = np.array(labels)
		self.K = K
		self.dist = dist
		self.KDTrees=KDTree(X,labels,self.dist)

	def predict(self,x,k):
		ans=self.KDTrees.search_knn(self.KDTrees.P,x,k)
		dc={}
		maxx=0
		y=0
		for i in range(ans.counter+1):
			if i==0:
				continue
			dc.setdefault(ans.heap[i].y,0)
			dc[ans.heap[i].y]+=1
			if dc[ans.heap[i].y]>maxx:
				maxx=dc[ans.heap[i].y]
				y=ans.heap[i].y
		return y
	def pred(self,test_x,k=None):
		'''
			test_x is a N*TM matrix,and indicate TM test case
			you can redecide the k
		'''
		if k==None:
			k=self.K
		test_case=np.array(test_x)
		y=[]
		for i in range(test_case.shape[1]):
			y.append(self.predict(test_case[:,i].transpose(),k))
		return y

       因为KNN毕竟是一个分类算法，所以我在predict是加上了分类的代码，如果只想检验Kd-tree的话，你可以直接用for_point()找最近k个点

五.测试+后记

       测试：

       我们选取《统计学习方法》上面的例子：

     

       使用代码：

          

X=np.array([[2,5,9,4,8,7],[3,4,6,7,1,2]])
y=np.array([2,5,9,4,8,7])
knn=KNNC(X,1,y)
print knn.for_point([[6.5],[7]],1)

X=np.array([[2,5,9,4,8,7],[3,4,6,7,1,2]])
y=np.array([2,5,9,4,8,7])
knn=KNNC(X,1,y)
print knn.for_point([[6.5],[7]],1)

这里y是label，是用来预测的，这个例子里没有实际作用，这是用来分类的

       输出中后面带了“===”的是扫描过的点，最后的是搜索的结果：

       

       我们可以看到的确避免扫描了(2,3)，Bingo！！

       我们再knn.for_point([[2],[2]])：可以看到避免扫了很多点！！！

      

      

       后记：

       从实现写此文前后耗时两天，昨天写代码写到熄灯且刚好测试通过，怎一个爽字了得！！最后，再在github上求个Star

reference：

【1】从K近邻算法、距离度量谈到KD树、SIFT+BBF算法 http://blog.csdn.net/v_july_v/article/details/8203674

【2】《统计学习方法》 李航

【3】最大堆的插入/删除/调整/排序操作(图解+程序)   http://www.java3z.com/cwbwebhome/article/article1/1362.html?id=4745

我自己的一点总结

#coding=utf-8

'''
Created on Sep 16, 2010
kNN: k Nearest Neighbors

Input:      inX: vector to compare to existing dataset (1xN)
            dataSet: size m data set of known vectors (NxM)
            labels: data set labels (1xM vector)
            k: number of neighbors to use for comparison (should be an odd number)
            
Output:     the most popular class label

@author: pbharrin

k-近邻算法
k-近邻算法采用测量不同特征值之间的距离方法进行分类

k-近邻算法的优缺点
优点 精度高 对异常值不敏感 无数据输入假定
缺点 计算复杂度高 空间复杂度高
适用数据范围： 数值型和标称型

标称型目标变量的结果只在有限目标集中取值，如真与假、动物分类集合{ 爬行类、鱼类、哺乳类、两栖类} ；数值型目标变量则可以从无限的数值集合中取值，如0.100、42.001、1000.743 等。

kNN算法的工作原理：
存在一个样本数据集合，也称作训练样本集，并且样本集中每个数据都存在标签。即我们知道样本集中每一数据与所属分类的对应关系
输入没有标签的新数据后，将新数据的每个特征和样本集中数据对应的特征进行比较，然后算法提取样本集中特征最相似的数据(最近邻)
和标签分类。一般来说，我们只选择样本数据集中前k个最相似的数据，这就是k-近邻算法的出处，通常k是不大于20的整数。最后，选择k
个最相似数据中出现次数最多的分类，作为新数据的分类




                  k-近邻算法的一般流程
(1)收集数据:可以使用任何方法。
(2)准备数据:距离计算所需要的数值，最好是结构化的数据格式。
(3)分析数据:可以使用任何方法。
(4)训练算法:此步骤不适用于k-近部算法。
(5)测试算法:计算错误率。
(6)使用算法:首先需要输入样本数据和结构化的输出结果，然后运行k-近邻算法判定输
  入数据分别属于哪个分类，最后应用对计算出的分类执行后续的处理。



从文本文件中解析数据
伪代码如下：
1、计算已知类别数据集中的点与当前点之间的距离
2、按照距离递增次序排列
3、选取与当前点距离最小的k个点
4、确定前k个点所在类别的出现频率
5、返回前k个点出现频率最高的类别作为当前点的预测分类


k-近邻算法是分类数据最简单有效的算法 k-近邻算法基于实例的学习，使用算法时，必须有接近实际数据的训练样本数据
k-近邻算法必须保存全部数据集，这样训练数据集很大的话，必须使用大量的存储空间。由于必须对数据集中每个数据计算距离值，实际使用时可能非常耗时
k-近邻算法的另一个缺陷是无法给出任何数据的基础结构信息，因此无法知晓平均实例样本和典型实例样本具有什么特征

numpy科学计算包
运算符模块
'''
from numpy import *
import operator
from os import listdir
'''距离的计算
classify0函数有4个输入参数：
用于分类的输入向量inX，输入的训练样本集为dataSet，标签向量labels，最后的参数k表示用于选择最近邻居的数目
其中标签向量的元素数目和矩阵dataSet的行数相同，使用欧氏距离公式，计算两个想亮点xA和xB之间的距离

计算两个向量点xA xB之间的距离
欧氏距离公式：
d=sqrt((xA0-xB0)^2+(xA1-xB1)^2)

计算完所有点之间的距离后，可以对数据按照从小到大的次序排列。然后，确定前K个距离最小元素所在的主要分类，输入K总是正整数；最后
将classCount()字典分解为元祖列表，然后使用程序第二行导数运算符模块的itermgetter方法，按照第二个元素
的次序对元祖进行排序。此处的排序为逆序，即按照从最大到最小次序排序，最后返回发生频率最好的元素标签
'''
def classify0(inX, dataSet, labels, k):
    dataSetSize = dataSet.shape[0] #数组的大小
    diffMat = tile(inX, (dataSetSize,1)) - dataSet #函数的形式是tile(A,reps)，参看博客
    sqDiffMat = diffMat**2  #**平方的意思
    sqDistances = sqDiffMat.sum(axis=1)
    distances = sqDistances**0.5 #开平方
    #按照距离递增次序排列  计算完所有点之间的距离后，可以对数据按照从小到大的次序进行排序，然后确定前k个距离最小元素所在的主要分类，输入k总是正整数；最后，将classCount字典分解为元祖列表，然后使用程序第二行导入运算符模块的itemgetter方法，按照第二个元素的次序对元祖进行排序  
    sortedDistIndicies = distances.argsort()
    
    classCount={}          
    for i in range(k):
        voteIlabel = labels[sortedDistIndicies[i]]
        classCount[voteIlabel] = classCount.get(voteIlabel,0) + 1
    sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)
    return sortedClassCount[0][0]

'''
有四组数，魅族数据有两个已知的属性或特征值，group矩阵每行包含一个不同的数据，可以把它想象成某个日志文件中
不同的测量点或者入口。因为人脑的限制，通常只能可视化处理三维以下的事务。因此为了实现数据可视化，对于每个
数据点通常只使用两个特征。
向量label包含每个数据点的标签信息，label包含的元素个数等于group矩阵行数
这里（1.0,1.1）定义为A (0,0.1)定义为B
'''
def createDataSet():
    group = array([[1.0,1.1],[1.0,1.0],[0,0],[0,0.1]])
    labels = ['A','A','B','B']
    return group, labels

'''
在约会网站上使用k-近邻算法
1、收集数据：提供样本文件
2、准备数据：使用Python解析文本文件
3、分析数据：使用matplotlib画二维扩散图
4、训练算法：此步骤不适合k-近邻算法
5、测试算法：测试样本和非测试样本区别在于：测试样本已经完成分类的数据，如果预测分类与实际类别不同，则标为error
6、使用算法：产生简单的命令行程序，然后可以输入一些特征数据以判断对方是否为自己喜欢的类型
'''
#确保样本文件和py文件在同一目录下，样本数据存放在datingTestSet.txt文件中
'''
样本主要包含了一下内容
1、每年获得的飞行常客里程数
2、玩视频游戏所耗时间百分比
3、每周消费的冰激凌公升数

>>> import matplotlib
>>> import matplotlib.pyplot as plt
>>> fig = plt.figure()
>>> ax = fig.add_subplot(111)
>>> ax.scatter(datingDataMat[:,1],datingDataMat[:,2])
<matplotlib.collections.PathCollection object at 0x03EF6690>
>>> plt.show()
由于没有使用样本分类的特征值，很难看到任何有用的数据模式信息，一般来说
采用色彩或者其他记号来标记不同样本分类，以便更好地理解数据信息
>>> ax.scatter(datingDataMat[:,1],datingDataMat[:,2,15*array(datingLabels),15*datingLabels])  暂时有误，需要解决
利用颜色以及尺寸标识了数据点的属性类别，带有养病呢分类标签的约会数据散点图，虽然能够比较容易的区分数据点从属类别，但依然很难根据这张图给出结论性的信息

'''



def file2matrix(filename):
    fr = open(filename)
    f_lines = fr.readlines()
    numberOfLines = len(f_lines)         #get the number of lines in the file 得到文件的行数
    
    returnMat = zeros((numberOfLines,3))        #prepare matrix to return  创建以0填充的矩阵numpy，为了简化处理，将该矩阵的另一维度设置为固定值3，可以根据自己的需求增加相应的代码以适应变化的输入值
    classLabelVector = []                       #prepare labels return   
    #fr = open(filename)
    
    index = 0
    for line in f_lines:   #循环处理文件中的每行数据，首先使用line.strip截取掉所有的回车字符，然后使用tab字符\t将上一步得到的整行数据分割成一个元素列表
        line = line.strip()
        
        listFromLine = line.split('\t')
        
        returnMat[index,:] = listFromLine[0:3]  #选取前3个元素，将其存储到特征矩阵中
        classLabelVector.append(listFromLine[-1]) #Python语言可以使用索引值-1表示列表中的最后一列元素，利用这种负索引，可以将列表的最后一列存储到向量classLabelVector中。注意：必须明确的通知解释器，告诉它列表中存储的元素值为整形，否则Python语言会将这些元素当做字符串来处理  listFromLine前不能加int否则报错
        index += 1
    return returnMat,classLabelVector

    
'''
归一化数值
多种特征同等重要时(等权重)，处理不同取值范围的特征值时，通常采用数值归一化，将取值范围处理为0~1或者-1~1之间
newValue = {oldValue-min}/(max-min)
min和max分别是数据及数据集中的最小特征值和最大特征值。虽然改变数值取值范围增加了分类器的复杂度，但为了得到精确结果，必须这样做
autoNorm将数字特征值转换为0~1
>>> reload(kNN)
<module 'kNN' from 'C:\Users\kernel\Documents\python\kNN.py'>
>>> normMat,ranges,minVals = kNN.autoNorm(datingDataMat)

函数autoNorm()中，将每列的最小值放在变量minValue中，将最大值放在变量maxValue中。其中
dataSet.min(0)中的参数0使得函数可以从列中选取最小值，而不是选取当前行的最小值。然后，
函数计算可能的取值范围，并创建新的矩阵。

为了归一化特征值，必须使用当前值减去最小值，除以取值范围。需要注意的是：特征值矩阵有1000*3
个值，而minVals和range的值都为1*3.使用Numpy库中tile()函数将变量内容复制成输入矩阵大
小的矩阵，具体特征值相除，而对于某些数值处理软件包，/可能意味着矩阵除法在Numpy同样库中，
矩阵除法需要使用函数linalg.solve(matA,matB)

'''
    
def autoNorm(dataSet):
    minVals = dataSet.min(0)  #每列的最小值  参数0可以从列中选取最小值而不是选取当前行的最小值
    maxVals = dataSet.max(0)  
    ranges = maxVals - minVals  #函数计算可能的取值范围，并创建新的返回矩阵，为了归一化特征值，必须使用当前值减去最小值，然后除以取值范围
    normDataSet = zeros(shape(dataSet))  #注意事项：特征值矩阵有1000*3个值。而minVals和range的值都为1*3.为了解决这个问题使用numpy中tile函数将变量内容复制成输入矩阵同样大小的矩阵
    m = dataSet.shape[0]
    normDataSet = dataSet - tile(minVals, (m,1))
    normDataSet = normDataSet/tile(ranges, (m,1))   #element wise divide
    return normDataSet, ranges, minVals
'''
对于分类器而言错误率就是分类器给出错误结果的次数除以测试数据的总数，完美分类器错误率为0，错误率为1的分类器不会给出任何正确的分类结果
在代码中设定一个计数器变量，每次分类器错误的分类数据，计数器就+1，程序执行完成后计算器的结果除以数据点总数即为错误率
>>> kNN.datingClassTest()
NameError: global name 'datingDataMat' is not defined  悬而未决
'''

   
def datingClassTest():
    hoRatio = 0;10

    datingDataMat,datingLables = file2matrix('datingTestSet.txt')
    normMat, ranges, minVals = autoNorm(datingDataMat)
    m = normMat.shape[0]
    numTestVecs = int(m*hoRatio)
    errorCount = 0.0
    for i in range(numTestVecs):
        classifierResult = classify0(normMat[i,:],normMat[numTestVecs:m,:],datingLabels[numTestVecs:m],3)
        print "the classifier came back with: %d, the real answer is: %d" % (classifierResult, datingLabels[i])
        if (classifierResult != datingLabels[i]): errorCount += 1.0
    print "the total error rate is: %f" % (errorCount/float(numTestVecs))
    print errorCount

'''
该方法有问题需要改正 (已作更正)

约会网站预测函数
'''
def classifyPerson():
    resultList = ['not at all','in small doses','in large doses']
    percentTats = float(raw_input(\
                  "percentage of time spent playing video games?"))
    ffMiles = float(raw_input("frequent flier miles earned per year?"))
    iceCream = float(raw_input("liters of ice cream consumed per year?"))
    datingDataMat,datingLabels = file2matrix('datingTestSet2.txt')
    normMat,ranges,minVals = autoNorm(datingDataMat)
    inArr = array([ffMiles,percentTats,iceCream])
    classifierResult = int(classify0((inArr-\
                                  minVals)/ranges,normMat,datingLabels,3))
    print "You will probably like this person:",\
          resultList[classifierResult - 1]


'''
手写识别系统
构造的系统只能识别数字0~9，需要是别的数字已经使用图像处理软件，处理成具有相同的色彩和大小：
宽高是32*32的黑白图像
1、收集数据 提供文本文件
2、准备数据 编写函数classify0(),将图像格式转换成分类器使用的list格式
3、分析数据 在Python命令提示符中检查数据，确保它符合要求
4、训练算法 此步骤不适合k-近邻算法
5、测试算法 测试样本和非测试样本区别在于：测试样本已经完成分类的数据，如果预测分类与实际类别不同，则标为error
6、使用算法 未实现
'''    
def img2vector(filename):
    returnVect = zeros((1,1024))
    fr = open(filename)
    for i in range(32):
        lineStr = fr.readline()
        for j in range(32):
            returnVect[0,32*i+j] = int(lineStr[j])
    return returnVect

'''

手写数字识别系统的测试代码

testDigits目录中的文件内容存储在列表中，然后可以得到目录中有多少文件，便将其存储到变量m中
创建一个m*1024的训练矩阵，该矩阵的每行数据存储一个图像，可以从文件名中解析出分类数字
该目录下的文件按照规则命名，如文件9_45.txt的分类是9，它是数字9的第45个实例
将类代码存储在hwLabels向量中，使用img2vector载入图像
对testDigits目录中的文件执行相似的操作，不同之处在于我们并不将这个目录下的文件载入矩阵中
而是利用classify0()函数测试该目录下每个文件，由于文件中的值已在0~1之间，所以不需要autoNorm()函数
该算法执行效率不高，因为算法需要为每个测试向量做2000词距离计算，每个距离计算包括了1024个维度浮点计算，总计执行900次
此外还需要为向量准备2M的存储空间  k决策树是k-近邻算法的改进版


'''
def handwritingClassTest():
    hwLabels = []
    trainingFileList = listdir('trainingDigits')           #load the training set
    m = len(trainingFileList)
    trainingMat = zeros((m,1024))
    for i in range(m):
        fileNameStr = trainingFileList[i]
        fileStr = fileNameStr.split('.')[0]     #take off .txt
        classNumStr = int(fileStr.split('_')[0])
        hwLabels.append(classNumStr)
        trainingMat[i,:] = img2vector('trainingDigits/%s' % fileNameStr)
    testFileList = listdir('testDigits')        #iterate through the test set
    errorCount = 0.0
    mTest = len(testFileList)
    for i in range(mTest):
        fileNameStr = testFileList[i]
        fileStr = fileNameStr.split('.')[0]     #take off .txt
        classNumStr = int(fileStr.split('_')[0])
        vectorUnderTest = img2vector('testDigits/%s' % fileNameStr)
        classifierResult = classify0(vectorUnderTest, trainingMat, hwLabels, 3)
        print "the classifier came back with: %d, the real answer is: %d" % (classifierResult, classNumStr)
        if (classifierResult != classNumStr): errorCount += 1.0
    print "\nthe total number of errors is: %d" % errorCount
    print "\nthe total error rate is: %f" % (errorCount/float(mTest))