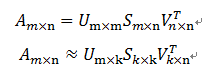A Singular Value Decomposition Approach For Recommendation Systems (4)
A Singular Value Decomposition Approach For
Recommendation Systems
说明:这是一篇来自土耳其中东技术大学的2010年的硕士论文,主要讲述了在推荐系统中应用SVD方法。
这篇文章可以到http://download.csdn.net/detail/yuzhongchun/8078769下载。
Chapter 4 Recommendation With SVD
4.1 Recommendation Using SVD
基于协同过滤的推荐算法面临诸如稀疏性、可扩展性和同义性(synonymy)等问题。为了去除一个大的又稀疏的数据集的噪声数据,提出了一些降维的方法。LSI(Latent SemanticIndexing, 隐语义索引)是一种广泛用于用户-物品评分矩阵降维的技术,能很好的应对协同过滤算法的挑战。基于SVD的推荐算法有很高的推荐质量,但计算比较复杂。
4.1.1 Dimensionality Reduction
SVD能提供原始矩阵的最好的低阶线性近似。通过选取最大的k个奇异值可以降低原始矩阵的纬度。k的值可能会根据数据的大小和结构而变化(《机器学习实战》一书第14章利用SVD简化数据中讲到一个典型的做法是保留矩阵中90%的能量信息,即将奇异值的平方和累加到总值的90为止)。
假设数据矩阵Data,纬度为m*n,即有m个用户,n个物品,SVD分解可以用下面的公示表示:
上面的公式中,Σ只有对角元素,其余元素都为0,此外,Σ的对角元素都是按照从大到小排列的,这些对角元素成为奇异值。
4.1.2 SVD Recommendation Algorithms
4.1.2.1 User-based Similarity
在推荐系统算法中一步关键的算法是计算用户之间的相似度,一般采用余弦相似度或欧氏距离。
基于用户相似度的SVD推荐算法
【问】评分矩阵A,已知User=x, Item=y, 请问Rating=?
1) 从原始矩阵A中找出对Item=y评过分的所有用户;
2) 使用降维矩阵,找出对Item=y评过分的与User=x最相近的那个User;
3) 从原始矩阵中获取最相似用户对Item=y的评分,并把这个评分当做User=x对Item=y的评分。
在第二步中,如果User=x已经在降维矩阵中,则按上面步骤计算;如果User=x是一个新的用户,在计算相似度之前,这个新用户必须冲n维空间投影到k维空间中。
如果知道SVD的空间几何意义,理解投影过程就很简单:原来的用户的评分向量Nu(1xn)是在V空间中(n维),将其与Vk矩阵相乘就知道这个用户向量的坐标,然后根据S进行坐标缩放(同时截取前k个值即可),获得的坐标就是用户的评分向量Nu在U空间中的坐标了。
用数学表达的话,设用户向量是Nu,投影到U空间后的向量为P,则有:
然后就可以计算这个用户(用P向量)与其他用户(Uk的各行向量)之间的相似度了。
大量的实验表明,计算相似度的话还是使用欧式距离比较有效。上面的算法瓶颈是如何在“茫茫人海”中找到最相似的那个User。
4.1.2.2 Item-based Similarity
使用基于物品的推荐不存在上面的计算瓶颈,因为我们探索的是物品之间的相似度而不是用户之间的相似度。在大多数系统中,物品比用户更稳定,不经常变化。所以,基于物品的相似度非常适合预计算。
相类似的,如果要计算两Item之间的相似度需要使用Vk矩阵。Vk 每一行代表一个Item,行之间越相近则代表Item之间越相似。其计算过程与上面所讲的User之间的推荐过程很接近。
基于物品相似度的SVD推荐算法
【问】评分矩阵A,已知User=x, Item=y, 请问Rating=?
1) 从原始矩阵A中找到被User=x评过分的那些items;
2) 使用降维矩阵,找出被User=x评过分的跟Item=y最相似的那个Item;
3) 从原始矩阵A中获取被User=x评过分的最相似的Item的评分,并把这个评分当做User=x对Item=y的评分。
与基于用户相似度推荐类似,在第二步计算中,如果Item=y已经在降维矩阵中,则可计算;如果Item=y是一个新物品,则要先做投影,然后再计算。
设新的Item评分向量是Ni(mx1),处于U空间(m维),需要投影到Vk空间(n维)。首先通过内积计算Ni在U空间中的坐标,然后使用Sk反向伸缩坐标即可得到在V空间的坐标。
用数学表达的话,设用户向量是Ni,投影到V空间后的向量为P,则有:
4.2 Incremental SVD
在一个推荐系统中,整个算法是分两步的。第一步是离线训练,第二步是在线执行。上面所讲述的用户相似度和物品相似度的计算都属于离线计算。一般的离线SVD对于m*n的矩阵,计算复杂度为,非常的费时。
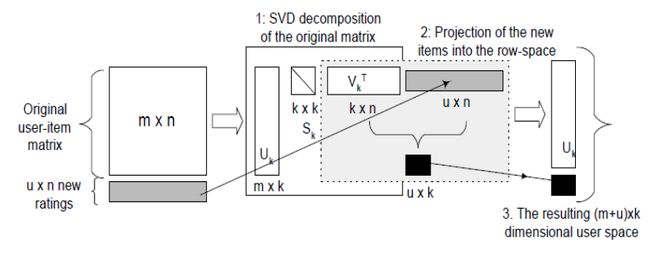
一个解决的方法是使用“folding-in”,进行增量SVD,如下图所示:
增量SVD的一个好处是不会影响之前存的的User或Item的坐标,当用户添加到已经分解的SVD模型中,所付出的时间复杂度仅为O(1)。
每次离线计算时再全部重新SVD,而线上运行时只进行增量SVD。
4.3 Contributions to SVD-based Recommendation
4.3.1 Categorization of Users and Items
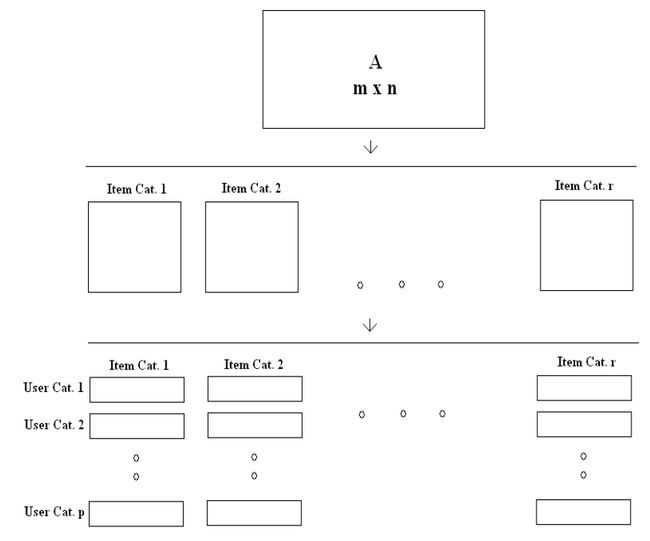
分类之后再逐个SVD,可以明显减少时间。
从原始矩阵我们可以得到r*p个矩阵。对这些矩阵,分别进行SVD。
基于分类数据(用户相似度)的SVD推荐算法
【问】评分矩阵A,已知User=x, Item=y, 请问Rating=?
1) 找出User=x的用户分类;
2) 找出Item=y的物品分类;
3) 这出这些分类对应的矩阵;
4) 在这个用户分类中找出对Item=y评过分的所有用户;
5) 在这个矩阵上进行SVD,找出与User=x最相似的用户;
6) 把最相似用户对Item=y的评分给Rating。
基于分类数据(物品相似度)的SVD推荐算法
【问】评分矩阵A,已知User=x, Item=y, 请问Raging=?
1) 找出User=x的用户分类;
2) 找出Item=y的物品分类;
3) 这出这些分类对应的矩阵;
4) 在这个物品分类中找出被User=x评过分的所有物品;
5) 在这个矩阵上进行SVD,找出与Item=y最相似的物品;
6) 把最相似物品的评分给Rating。
4.3.2 Adopting Tags to SVD Recommendation
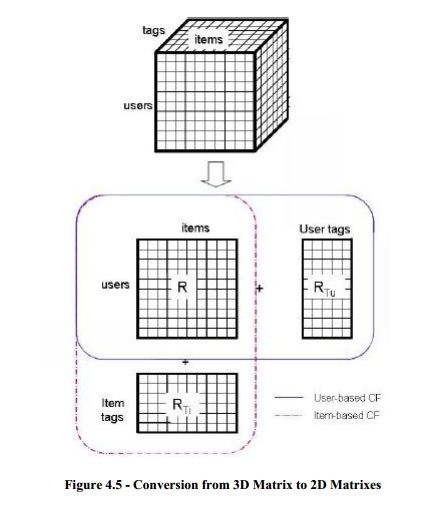
为了提高推荐质量,一些元信息例如物品的内容信息已经被用作额外的知识。随着一些允许用户写物品标签的系统的流行,标签成为了一个对推荐算法很有用的信息。本文把标签引入到推荐算法中,为了使标签能适合一般的SVD算法,我们把三维矩阵<user, item, tag>降成三个二维矩阵<user, item>,<user, tag>,<item, tag>。
4.3.2.1 Extension with Tags
用户标签是用户u写的来标记物品的,可以被看成用户物品矩阵中的物品。物品标签是用户描述物品i的标签,扮演者用户物品矩阵中的用户角色。
另外,聚类方法也可以应用到标签中以使类似的标签聚类到一块。在本文中,作者使用子字符串,java字符串比较和编辑距离(edit distance)计算方法来聚类相类似的标签,以提高推荐的性能。
Edit Distance
在信息理论和计算机科学中,两个字符串的edit distance是一个字符串转换为另一个字符串所需要的操作数。有一些不同的方法来定义edit distance,相对应的有不同的算法去计算它的值。在本文中,作者使用”Levenshtein Distance”。
例如,”kitten”和”sitting”的Levenshtein Distance,如下所示:
1.kitten –> sitten (substitutionof ‘s’ for ‘k’)
2.sitten -> sittin (substitutionof ‘i’ for ‘e’)
3.sittin -> sitting (insert‘g’ at the end)