多核计算与程序设计 - 09 基本算法和数据结构 之四 AVL搜索树

AVL搜索树

AVL 树概念：一个自平衡的二叉树，左右子树的高度的差不超过1。它的名字得名于它的发明者G.M. Adelson-Velsky 和 E.M. Landis。

AVL搜索树操作   之   插入操作

插入操作的关键点是找到离插入点最近的，并且因为插入新的节点而成为不平衡节点的点。这里且把它称为A节点。

基本情况：找到二叉树不平衡的节点，然后对它进行选择，得到平衡的二叉树。

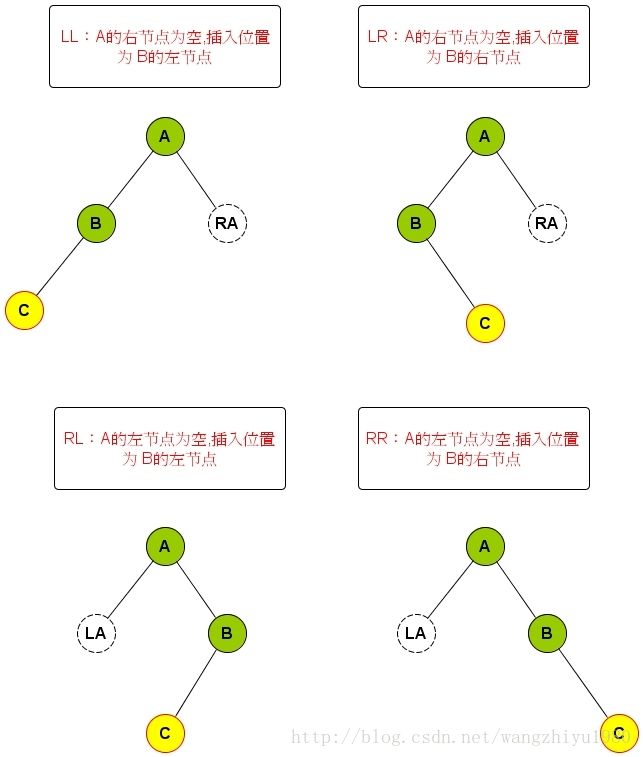
不平衡的四种情况：LL  LR  RL  RR 图中 A为操作节点，B为子节点，C为插入节点，这几种情况都会造成树的不平衡。

这里关于A节点的定义，

所以在节点的插入时，要对这几种情况进行处理。保证插入后，树仍为平衡二叉树。

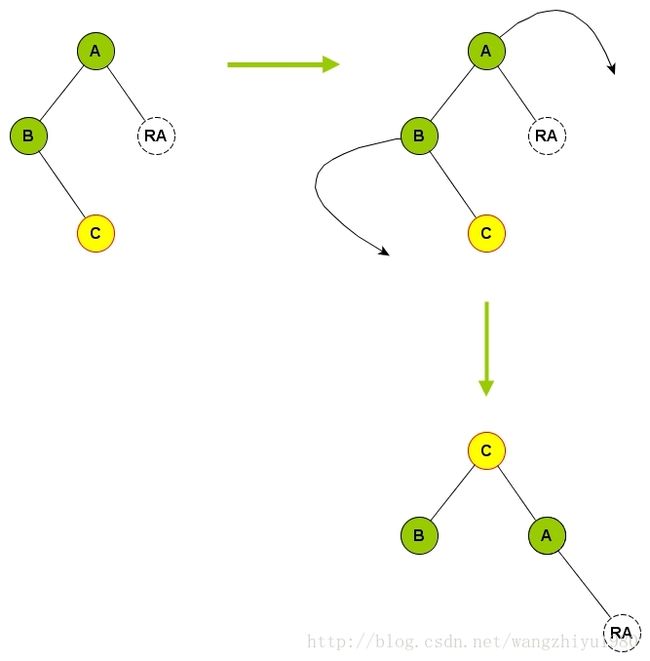
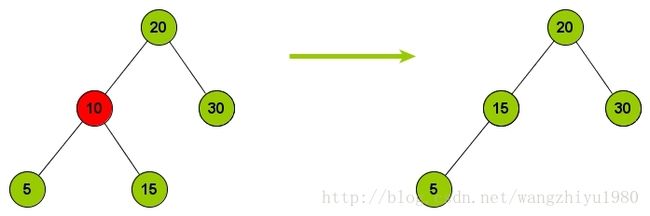
插入时处理 LL 的情况：主要是把A 节点右旋

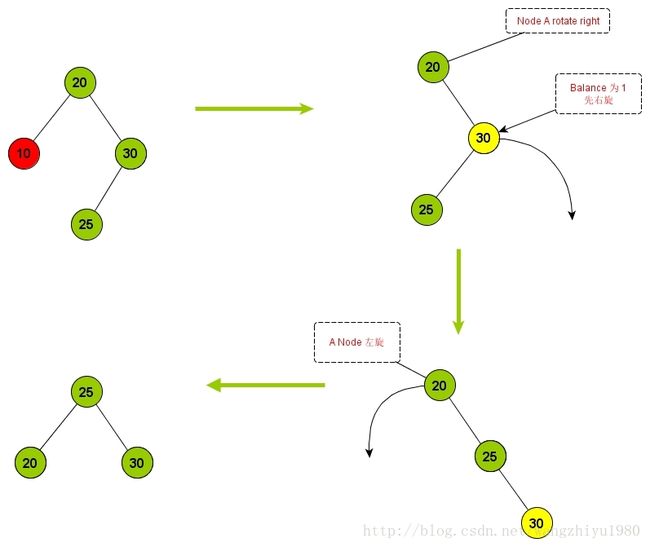
插入时处理 LR 的情况：主要是把A节点右旋，B节点左旋

LL 算法

void LL()
{
    B节点 = A 节点的左节点
    A节点右旋
    调整B节点到插入节点的平衡因子
    A节点平衡因子 = 0
    B节点平衡因子 = 0
}

LR 算法

void LR
{
    B节点 = A 节点的左节点
    C节点 = B 节点的右节点
    
    if (插入节点在 C的左子树)
    {
        C节点的平衡因子 + 1
    }
    if else (插入节点在 C的右子树)
    {
        C节点的平衡因子 - 1
    }
    else  // C节点就是插入节点
    {
        C节点的平衡因子为 0
    }
    
    B节点左旋
    A节点右旋
    
    C节点平衡因子 = 0
    if (插入节点在 C的左子树)
    {
        调整B节点到插入节点的平衡因子
    }
    if else (插入节点在 C的右子树)
    {
        调整A节点到插入节点的平衡因子
    }
    else  // C节点就是插入节点
    {
        不用调整
    }
}

RR  RL  和  LL  LR刚好对称操作

插入节点的伪代码

void Insert(pRoot, pNewNode)
{
    if (pRoot == NULL)
    {
        pRoot = pNewNode;
        return;
    }
    找到 A节点
    
    if (A节点不存在)  //二叉树是一颗完全平衡的二叉树
    {
        找到插入pNewNode的位置
        插入节点
        从根节点到插入节点调整他们的平衡因子
        return;
    }
    
    // A节点少一个节点，插入新节点后刚好平衡
    if ((A 节点存在) && 
        ((A的平衡因子为1, 插入位置为A的右节点) || (A的平衡因子为-1, 插入位置为A的左节点)))
    {
        插入pNewNode;
        A节点的平衡因子 = 0;
        return;
    }

    if (插入在 A的左子树)
    {
        B节点=A的左节点
        if (插入在B的左子树)
        {
            LL()
        }
        else
        {
            LR()
        }
    }
    
    if (插入在 A的右子树)
    {
        B节点=A的右节点
        if (插入在B的左子树)
        {
            RL()
        }
        else
        {
            RR()
        }
    }
}

AVL搜索树操作   之  删除操作

删除操作要比插入操作复杂些，涉及到的情况也比较多。

首先要删除一个节点，它的子树可能有这么几种情况

1. 左子树 或 右子树不存在
2. 左 右子树都不存在
3. 左 右子树都存在

删除节点的左子树或又子树不存在

删除节点的左右子树都不存在

删除节点的左右子树都存在

删除过程中A节点的定义已经有所改变，它并不是离删除节点最近的不平衡节点，而是最需要调整的节点。

那么对应着上面几种情况，把一个节点删除后，它的A 节点的平衡因子可能有这么几种情况：

1. balance =0
2. balance = -1 或 balance = 1
3. balance = -2 或 balance = 2

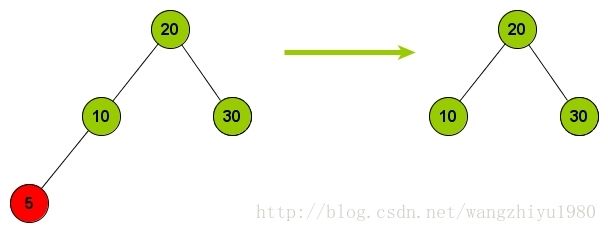
当 balance = -2 或 balance = 2 时则需要对树进行调整。

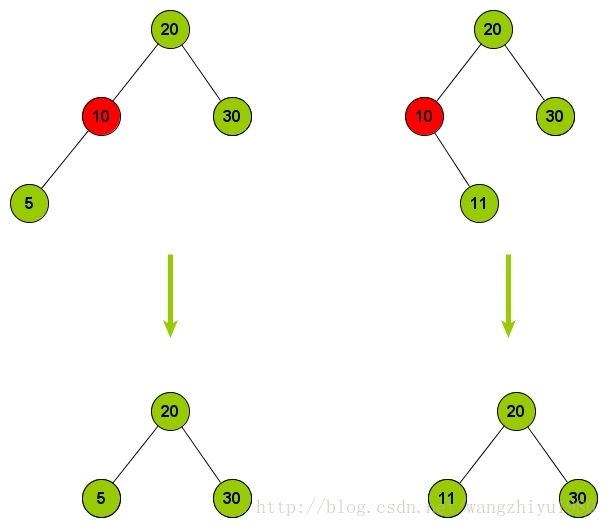
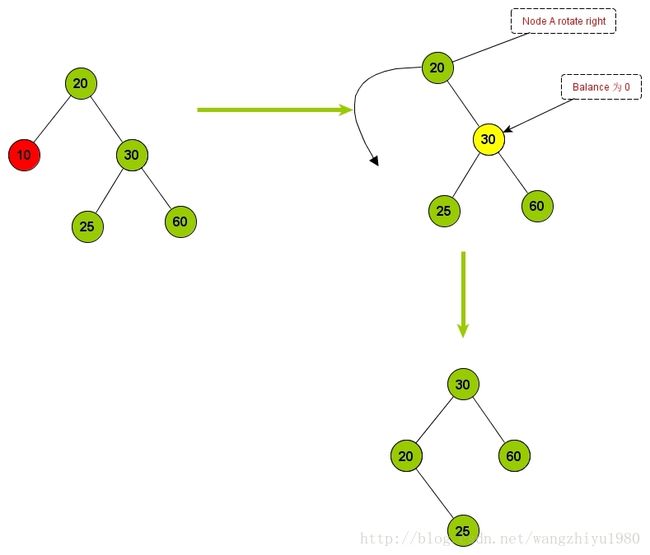
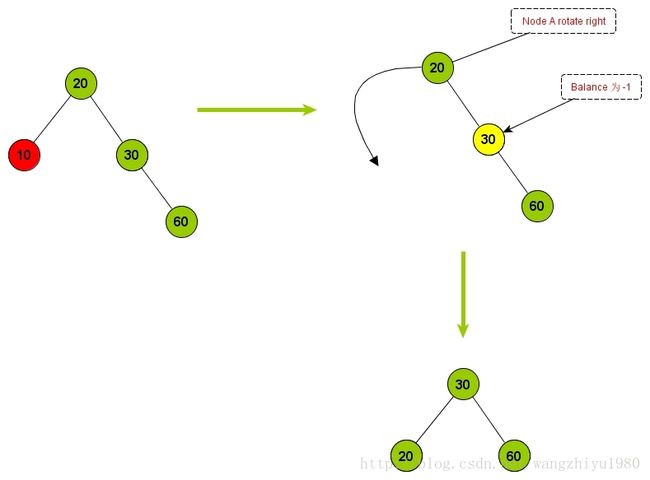
当 Node A的balance 为 -2时，按照NodeB的Balance的值又划分为3种情况 (balance = 0, balance = -1, balance = 1)。按照这三种情况对树进行旋转处理。

L0：

L1：

L-1：

代码实例