5.1 数组
C++为基本的数据类型(整数,浮点数,字符型和布尔型)提供了内置的支持(就像在上一章我们为复数类定义了重载的运算符那样),内置的支持也称为协助函数(helper function),支持这些数据类型完成各种允许的运算。
也就是说基本数据类型也可以说是一个类:有数据有操作,两者是封装起来的。
在C++的标准库中支持基本类抽象的组合,如字符串,复数等。在内置数据类型和标准库类类型之间是复合类型(Compound type),特别是指针和数组类型。
下面给出一实例:
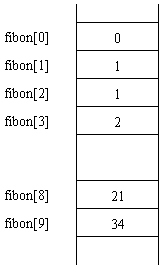
int fibon[10]={0,1,1,2,3,5,8,13,21,34};
数组名为fibon,是一个包含10个元素的整型一维(dimension)数组,其第1个元素为fibon[0],存放0,最后一个元素为fibon[9],存放34。
对数组元素的访问是通过下标(subscript)操作符,按元素在数组中的位置进行访问,称为 索引访问 (indexing)或 下标访问 (subscripting)。数组元素的访问示意图如下图所示。
注意:
结构数组定义 :
struct keyword {
char word[16]; //关键字
int count; //该关键字将在源程序中出现的次数
};
初始化:
keyword keytab[]={"auto", 0,"break", 0,"case", 0,"char", 0,
……"unsigned", 0,"volatile", 0,"while", 0,};
结构数组初始化时可以用括号来区分每一个结构,例如:
keyword keytab[]={{"auto", 0},{"break", 0},{"case", 0},……};
当提供了数组中所有结构值时,不必用这种括号的形式。
对象数组定义 :
CGoods goods[3];
该商品类对象数组包含3个商品对象数组元素,系统调用3次默认的构造函数来建立这3个商品对象数组元素。
初始化: 应该完整书写各个元素的构造函数及成员数据初值:
CGoods goods[3]={
CGoods("夏利2000",30,98000.0), //调用三参数构造函数,初始化goods[0]
CGoods("桑塔纳2000",164000.0), //调用两参数构造函数,初始化goods[1]
CGoods() //调用默认的构造函数,初始化goods[2]
};
C++只传递数组首地址,而对数组边界不加检查。这带来的好处是,函数对长度不等的同类数组都通用。如要指定长度可以设定另一个参数来传递数组元素的个数。
【例5.2】字符数组与字符数组相连接。
#include <iostream>
using namespace std;
void strcat(char s[],char ct[]){
int i=0,j=0;
while (s[i]!=0) i++;
while (ct[j]!=0) s[i++]=ct[j++];
s[i]='\0';
}
int main (void){
char a[40]="李明";
char b[20]="是东南大学学生";
cout<<a<<endl;
cout<<b<<endl;
strcat(a,b);
cout<<"字符串连接后:"<<endl;
cout<<a<<endl; //打印字符数组a
return 0;
}
回溯法应用广泛,八皇后问题、迷宫问题、四色地图等等都可以用回溯法求解。
【例5.3】八皇后问题:在8×8的国际象棋棋盘上安放八个皇后,为避免她们之间相互攻击,要求没有任何两个皇后在棋盘的同一行、同一列及在同一对角线上。图6.4是八皇后问题的一个解。八皇后在棋盘上可能有的布局数是:C864=64!/(8!×56!)=4426165368种,用回溯法解决八皇后问题显然是合适的。
#include <iostream>
#include <cmath>
using namespace std;
int main(){
int queen[8];
int total = 0; //方案计数
int i, j, k;
for (i=0;i<8;i++) queen[i] = 0; //八皇后全放在第0列
for (i=1;;){ //首先安放第0行皇后
if(queen[i]<8){ //皇后还可调整
k=0; //检查与第k个皇后是否互相攻击
while(k<i&&(queen[k]-queen[i])&&(abs(queen[k]-queen[i])-abs(k-i))) k++;
if (k<=i-1){ //与第k个皇后互相攻击
queen[i]++; //第i个皇后右移一列,重测
continue;
}
i++; //无冲突,安置下一行皇后
if(i<8) continue;
for(j=0;j<8;j++) cout<<queen[j]; //已完成,输出结果
cout<<" ";
total++; //方案数加1
if(total%5==0) cout<<endl;
queen[7]++; // 将第7个皇后右移一列,前7个不动
i=7; //此处是制造机会,如不成功则回溯,关键一步
}
else //当前行皇后无法安置,回溯
{
queen[i]=0; //当前行皇后回归0列
i--; //回溯到前一行皇后
if(i<0){ //回溯到数组0行之前,结束
cout<<" 总数:"<<total<<endl;
return 0;
}
else queen[i]++; //前一行皇后右移一列
}
}
}
数组、数组元素及其存储方式
数组(array)是一种顺序容器sequence container,是由单一类型元素组成的一个有序集合。下面给出一实例:
int fibon[10]={0,1,1,2,3,5,8,13,21,34};
数组名为fibon,是一个包含10个元素的整型一维(dimension)数组,其第1个元素为fibon[0],存放0,最后一个元素为fibon[9],存放34。
对数组元素的访问是通过下标(subscript)操作符,按元素在数组中的位置进行访问,称为 索引访问 (indexing)或 下标访问 (subscripting)。数组元素的访问示意图如下图所示。

注意:
- 数组是一种组合类型,是不能作为一个整体进行访问和处理的,只能按元素进行个别的访问和处理。(字符串例外!)
- C++数组第一个元素的下标为0,而不是1,且下标表达方式是固定的。
- 数组元素在内存中是从低地址开始顺序排列,各元素的存储单元占用内存大小相同,各元素的存储单元之间没有空隙,可以从数组第一个元素存储单元的起始地址计算出任意一个元素存储单元的起始地址。
结构数组定义 :
struct keyword {
char word[16]; //关键字
int count; //该关键字将在源程序中出现的次数
};
初始化:
keyword keytab[]={"auto", 0,"break", 0,"case", 0,"char", 0,
……"unsigned", 0,"volatile", 0,"while", 0,};
结构数组初始化时可以用括号来区分每一个结构,例如:
keyword keytab[]={{"auto", 0},{"break", 0},{"case", 0},……};
当提供了数组中所有结构值时,不必用这种括号的形式。
对象数组定义 :
CGoods goods[3];
该商品类对象数组包含3个商品对象数组元素,系统调用3次默认的构造函数来建立这3个商品对象数组元素。
初始化: 应该完整书写各个元素的构造函数及成员数据初值:
CGoods goods[3]={
CGoods("夏利2000",30,98000.0), //调用三参数构造函数,初始化goods[0]
CGoods("桑塔纳2000",164000.0), //调用两参数构造函数,初始化goods[1]
CGoods() //调用默认的构造函数,初始化goods[2]
};
数组名作为函数参数
数组名可以作为函数的参数。在函数调用时传递实参数组的首地址,所以在被调函数中对形参数组的处理实际就是对调用函数的实参数组的处理。C++只传递数组首地址,而对数组边界不加检查。这带来的好处是,函数对长度不等的同类数组都通用。如要指定长度可以设定另一个参数来传递数组元素的个数。
【例5.2】字符数组与字符数组相连接。
#include <iostream>
using namespace std;
void strcat(char s[],char ct[]){
int i=0,j=0;
while (s[i]!=0) i++;
while (ct[j]!=0) s[i++]=ct[j++];
s[i]='\0';
}
int main (void){
char a[40]="李明";
char b[20]="是东南大学学生";
cout<<a<<endl;
cout<<b<<endl;
strcat(a,b);
cout<<"字符串连接后:"<<endl;
cout<<a<<endl; //打印字符数组a
return 0;
}
数组的应用——回溯算法
回溯法的基本思想是:通过对问题的分析找出解决问题的线索,先在一个局部上找出满足问题条件的局部的解,然后逐步由局部解向整个问题的解的方向试探,若试探成功就得到问题的解,试探失败逐步向后退,改变局部解再向前试探。回溯法能避免枚举法的许多不必要的搜索,使问题比较快地得到解决。回溯法应用广泛,八皇后问题、迷宫问题、四色地图等等都可以用回溯法求解。
【例5.3】八皇后问题:在8×8的国际象棋棋盘上安放八个皇后,为避免她们之间相互攻击,要求没有任何两个皇后在棋盘的同一行、同一列及在同一对角线上。图6.4是八皇后问题的一个解。八皇后在棋盘上可能有的布局数是:C864=64!/(8!×56!)=4426165368种,用回溯法解决八皇后问题显然是合适的。
#include <iostream>
#include <cmath>
using namespace std;
int main(){
int queen[8];
int total = 0; //方案计数
int i, j, k;
for (i=0;i<8;i++) queen[i] = 0; //八皇后全放在第0列
for (i=1;;){ //首先安放第0行皇后
if(queen[i]<8){ //皇后还可调整
k=0; //检查与第k个皇后是否互相攻击
while(k<i&&(queen[k]-queen[i])&&(abs(queen[k]-queen[i])-abs(k-i))) k++;
if (k<=i-1){ //与第k个皇后互相攻击
queen[i]++; //第i个皇后右移一列,重测
continue;
}
i++; //无冲突,安置下一行皇后
if(i<8) continue;
for(j=0;j<8;j++) cout<<queen[j]; //已完成,输出结果
cout<<" ";
total++; //方案数加1
if(total%5==0) cout<<endl;
queen[7]++; // 将第7个皇后右移一列,前7个不动
i=7; //此处是制造机会,如不成功则回溯,关键一步
}
else //当前行皇后无法安置,回溯
{
queen[i]=0; //当前行皇后回归0列
i--; //回溯到前一行皇后
if(i<0){ //回溯到数组0行之前,结束
cout<<" 总数:"<<total<<endl;
return 0;
}
else queen[i]++; //前一行皇后右移一列
}
}
}