HDU 1277 Fast Food
Problem Description
The fastfood chain McBurger owns several restaurants along a highway. Recently, they have decided to build several depots along the highway, each one located at a restaurant and supplying several of the restaurants with the needed ingredients. Naturally, these depots should be placed so that the average distance between a restaurant and its assigned depot is minimized. You are to write a program that computes the optimal positions and assignments of the depots.
To make this more precise, the management of McBurger has issued the following specification: You will be given the positions of n restaurants along the highway as n integers d1 < d2 < ... < dn (these are the distances measured from the company's headquarter, which happens to be at the same highway). Furthermore, a number k (k <= n) will be given, the number of depots to be built.
The k depots will be built at the locations of k different restaurants. Each restaurant will be assigned to the closest depot, from which it will then receive its supplies. To minimize shipping costs, the total distance sum, defined as
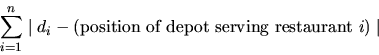
must be as small as possible.
Write a program that computes the positions of the k depots, such that the total distance sum is minimized.
To make this more precise, the management of McBurger has issued the following specification: You will be given the positions of n restaurants along the highway as n integers d1 < d2 < ... < dn (these are the distances measured from the company's headquarter, which happens to be at the same highway). Furthermore, a number k (k <= n) will be given, the number of depots to be built.
The k depots will be built at the locations of k different restaurants. Each restaurant will be assigned to the closest depot, from which it will then receive its supplies. To minimize shipping costs, the total distance sum, defined as
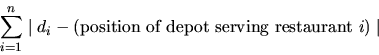
must be as small as possible.
Write a program that computes the positions of the k depots, such that the total distance sum is minimized.
Input
The input file contains several descriptions of fastfood chains. Each description starts with a line containing the two integers n and k. n and k will satisfy 1 <= n <= 200, 1 <= k <= 30, k <= n. Following this will n lines containing one integer each, giving the positions di of the restaurants, ordered increasingly.
The input file will end with a case starting with n = k = 0. This case should not be processed.
The input file will end with a case starting with n = k = 0. This case should not be processed.
Output
For each chain, first output the number of the chain. Then output a line containing the total distance sum.
Output a blank line after each test case.
Output a blank line after each test case.
Sample Input
6 3 5 6 12 19 20 27 0 0
Sample Output
Chain 1 Total distance sum = 8
Source
Southwestern Europe 1998
用dp[i][j]表示前j个饭店建第i个仓库的最短路径。dp[i][j]=min{dp[i-1][k]+cost[k+1][j]},
且i-1<=k<j。cost[i][j]表示在i到j之间建一个仓库的最小路径,要在i~j之间建立一个仓库,那么
必须建立在下标为(i+j)/2的饭店。
- #include<iostream>
- #include<cmath>
- using namespace std;
- int main()
- {
- int n,m;
- int i,j,k,t=0;
- int dp[202][202],cost[202][202];
- int food[202];
- //freopen("in.txt","r",stdin);
- while(scanf("%d%d",&n,&m),n+m)
- {
- t++;
- for(i=1;i<=n;i++)
- scanf("%d",&food[i]);
- memset(cost,0,sizeof(cost));
- for(i=1;i<=n;i++)
- {
- for(j=i;j<=n;j++)
- {
- for(k=i;k<=j;k++)
- {
- cost[i][j]+=abs(food[k]-food[(i+j)/2]);
- }
- }
- }
- memset(dp,0,sizeof(dp));
- for(i=1;i<=n;i++)
- {
- dp[1][i]=cost[1][i];
- }
- for(i=2;i<=m;i++)
- {
- for(j=i+1;j<=n;j++)
- {
- int Min=0xfffffff;
- for(k=i-1;k<j;k++)
- {
- if(Min>dp[i-1][k]+cost[k+1][j])
- {
- Min=dp[i-1][k]+cost[k+1][j];
- }
- }
- dp[i][j]=Min;
- }
- }
- printf("Chain %d/n",t);
- printf("Total distance sum = %d/n",dp[m][n]);
- printf("/n");
- }
- return 0;
- }