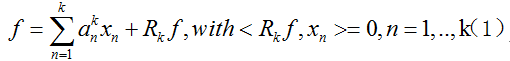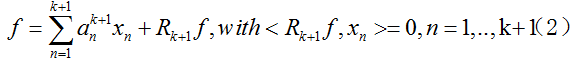稀疏编码最优化解法

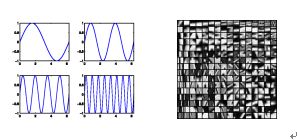
稀疏编码的概念来自于神经生物学。生物学家提出，哺乳类动物在长期的进化中，生成了能够快速，准确，低代价地表示自然图像的视觉神经方面的能力。我们直观地可以想象，我们的眼睛每看到的一副画面都是上亿像素的，而每一副图像我们都只用很少的代价重建与存储。我们把它叫做稀疏编码，即Sparse Coding.

稀疏编码的目的是在大量的数据集中，选取很小部分作为元素来重建新的数据。

稀疏编码难点之一是其最优化目标函数的求解。

这篇文章先做一个概述，接着再分别讨论各个解法。

 

稀疏线性模型

X为一个n为特征向量，可以是一个小波信号，可以是一副图片等。

D为标准化的基础矩阵，由组成元素的基本原子构成，也称为字典。在信号中可以是不同频率的波形，在图像中可以是构成图像的基本边，角。

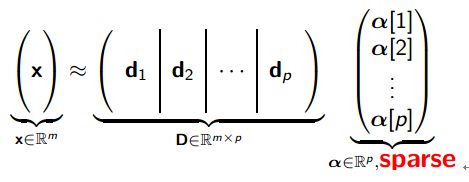
X可以由D中和少量原子线性组合而成，及其表示系数为稀疏。如下：

 

数学模型

引出稀疏表示的两个基本要求，1是尽可能与原特征相似，2是系数为稀疏。

上式中，我们要求p>m，根据线性代数的知识我们知道，稀疏系数有无穷多组的解。根据稀疏的条件，我们可以在所有的可行解中挑出非零元素最少的解，也就是满足稀疏性。于是得到如下的数学模型：

 

如果再考虑噪声的话，就得到如下的模型：

 

目标函数中为零范数约束，是NP难题。

有人做了一个证明，在一定条件下，上述的最优化问题有唯一的解。

Terry tao又证明了，在满足一定条件下，零范数问题与一范数问题是等价的。于是上述模型转化为：

 

基于上面的思想，还有各种不同版本的数学模型。

常见模型

我们知道上式为非凸优化问题，常用的解法有：greedy algorithm，代表有Matching Pursuit, Orthogonal Matching Pursuit

上式为解不等式约束问题，常用的解法：LASSO

再写成拉格朗日乘子的形式，如果已知lambda，可用soft thresholding方法，常见的还有coordinate descent, Bregman Iteration等；

如果未知lambda，则用Homotopy.

 

 

MP算法与OMP算法

分类： 机器学习 2014-01-17 13:40  124人阅读  评论(0)  收藏  举报

MP算法 OMP算法

目录(?)[+]

稀疏编码的一般最优化公式为：

其中的零范数为非凸优化。那么如何解这么一个非凸优化问题呢？其中一个常用的解法就是MP算法。

MP算法

MP算法是一种贪心算法（greedy），每次迭代选取与当前样本残差最接近的原子，直至残差满足一定条件。

求解方法

首先解决两个问题，怎么定义“最接近原子”，怎么计算残差？

选择最接近残差的原子：MP里定义用向量内积原子与残差的距离，我们用R表示残差，di表示原子，则：

Max[Dist(R,di)]=max[<R,di>];

残差更新：R=R-<R,di>I;继续选择下一个，直至收敛；

需要注意的是，MP算法中要求字典原子||di||=1,上面的公式才成立。

我们用二维空间上的向量来表示，用如下的图来表述上面的过程：

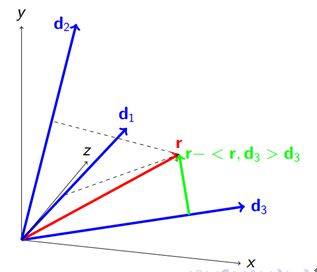
上图中d1,d2,d3表示归一化的原子，红色向量r表示当前残差；

进过内积计算，<r,d3>最大，于是r分解为d3方向以及垂直于d3方向的两个向量(<r,d3>d3及r-<r,d3>d3)，把d3方向的分量（<r,d3>d3）加入到已经求得的重构项中，那么绿色向量（r-<r,d3>d3）变为新的残差。

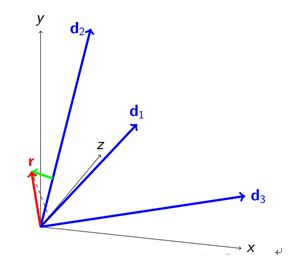
再一轮迭代得到如下：

R往d1方向投影分解，绿色向量成为新的残差。

 

具体算法：

 

收敛性

从上面的向量图我们可以清楚地看出，k+1的残差Rk+1是k步残差Rk的分量。根据直角三角形斜边大于直角边，|Rk+1|<=|Rk|，则算法收敛。

注意事项：

1.上面也讲过，字典的原子是归一化的，也就是||di||=1，因为我们选取max<R,di>时，如果di长度不统一，不能得出最好的投影。

2.如果我们的字典只有两个向量d1,d2,那么MP算法会在这两个向量间交叉迭代投影，也就是f=a1d1+a2d2+a3d1+a4d2+…..;也就是之前投影过的原子方向，之后还有可能投影。换句话说，MP的方向选择不是最优的，是次优的。

如下图：

这也是其改进版本OMP要改进的地方。

 

OMP算法 （ smit正交化）

也就是正交的MP算法。

MP算法的次最优性来源其残差只与当前投影方向垂直，这样在接下来的投影中，很有可能会再次投影到原来的方向。

于是，在投影时，如果我们使得残差Rk+1与x1-xk+1的所有向量垂直，则可以克服这个问题，如下：

 

求解方法

假设我们已经得到了第k步的最优解：

我们要继续更新到第k+1步，目标是得到：

需要注意的是，我们下一步更新时，之前原子的系数 也要更新，否则不能满足约束。

于是我们需要求得如何更新之前原子系数 ，以及如何求得下一个投影方向 。

 

收敛性：

同样根据勾股定理，得到如下：

于是算法收敛。

 

具体步骤：

 

最后，贴一个sparse求解的工具包，里面包含了MP，OMP算法的代码：

http://spams-devel.gforge.inria.fr/

 

参考文献：

http://lear.inrialpes.fr/people/mairal/tutorial_iccv09/

http://blog.csdn.net/scucj/article/details/7467955

OrthogonalMatching Pursuit:Recursive Function Approximation with Applications to WaveletDecomposition