扩展KMP算法实现
对于字符串S和T,n=|S|,m=|T|。要求S(i,n)与T的最长公共前缀长度(i=1,2...n)。
用B[i]表示该长度,那么S(i,n)与T的最长公共前缀即S(i,i+B[i]-1)。
暴力枚举所用时间为O(nm),慢的原因是计算了很多冗余情况。如:
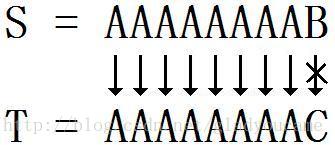
S = AAAAAAAAB, T = AAAAAAAAC
那么,第一次比较了9位。
实际上前几位“A”是不需要再比较的。
扩展KMP算法即利用已得到的信息来减少冗余的比较。
首先,设A[i]为T与T(i,n)的最长公共前缀。求出A后即可用类似的方法求B。现在假设我们已求得A[2]...A[i-1](A1=n),其中,设k满足k+A[k]-1在所有j+A[j]-1(1<j<i)中有最大值。当k+A[k]-1>i+A[i-k+1]-1时,情况如下图所示:

图中,相同颜色表示的子串相同(黑色除外)。即:T(1,A[k]) = T(k,k+A[k]-1),T(1,A[w]) = T(w,w+A[w]-1) = T(i,i+A[w]-1),T(i+A[w]) = T(w+A[w]) ≠ T(Aw+1)。如此,可知A[i] = A[w]。
当k+A[k]-1<=i+A[w]-1时,设L=k+A[k]-i我们尚未知道T(L)与T(i+L)是否相等,向后逐字符比较T(L+x)与T(i+L+x),直到两个值不等,此时可知A[i] = L+x,并可更新k值。
从整体分析,k值是不减的,故求出A数组的时间为O(m)。
求B数组时,同样的:
当k+B[k]-1 > i+A[i-k+1]-1时,令B[i] = B[i-k+1];
当k+B[k]-1 <=i+A[i-k+1]-1时,设L=k+B[k]-i向后逐字符比较T(L+x)与S(i+L+x),两值不等时令B[i]=L+x,并更新k值。
扩展KMP的总时间为O(n+m)
typedef long long lld;
const int INF = 1000000000;
const int MAX = 1000005;
int a[MAX];
int b[MAX];
char S[MAX], T[MAX];
//a[i] 为T与T(i,n)的最长公共前缀长度
//b[i] 为T与S(i,n)的最长公共前缀长度
void get_fail(char *S, char *T, int n, int m)
{
int i, j = 0;
a[0] = m; //第一个公共前缀长度必然为m
while (1 + j < m && T[j] == T[1 + j])
j++;
a[1] = j;
int k = 1; //k上一次计算的起始位置
int need = 0;
for (i = 2; i < m; i++)
{
need = k + a[k] - i; //判断是否需要计算
//cout << "i: " << i << " k:" <<k << " need: " << need << endl;
if (a[i - k] < need)
a[i] = a[i - k];
else
{
j = 0 > need ? 0 : need;
while (i + j < m && T[j] == T[j + i])
j++;
a[i] = j; //计算的j 为公共前缀的长度
k = i;
}
}
j = 0;
while (j < n && j < m && S[j] == T[j])
j++;
b[0] = j;
k = 0;
for (i = 1; i < n; i++)
{
need = k + b[k] - i;//k记录前面的最大位置
//cout << "i: " << i << " k:" <<k << " need: " << need << endl;
if (a[i - k] < need)
b[i] = a[i - k];
else
{
j = 0 > need ? 0 : need;
while (i + j < n && j < m && S[i + j] == T[j])
j++;
b[i] = j;
k = i;
}
}
}
//start 提示:自动阅卷起始唯一标识,请勿删除或增加。
int main()
{
int n, m;
int last = 0;
int i, j, k;
freopen("in.txt", "r", stdin);
while (scanf("%s%s", &S, &T) != EOF)
{
n = strlen(S);
m = strlen(T);
get_fail(S, T, n, m);
// for(int i=0; i<=10; i++)
// cout << a[i] << " ";
// cout << endl;
// for(int i=0; i<=10; i++)
// cout << b[i] << " ";
// cout << endl;
int ans = 0;
for (i = 0; i < n; i++)
{
if (b[i] == n - i)
{
ans = b[i];
break;
}
}
printf("%d\n", ans);
}
return 0;
}
测试数据:
abcde cdefg
abcdab dacdacg