matlab心形图大全，几个经典的函数图像，有趣的函数图像，matlab画图

收藏几个经典的函数，用来当作数学优化方法求解的例子。再收藏几个有趣的函数图像。

1 平面心形图像

经过 网上搜索，平面坐标系中，下面函数最想心形图像，而且函数形式简单，不需要分段。

     

改变右面的数值可以变化心形图像的大小。

> ezplot('x^2+(y-(x^2)^(1/3))^2=9')

还有一个函数：

                         

ezplot('-x^2*y^3+(x^2+y^2-1)^3=0',[-1.5,1.5])

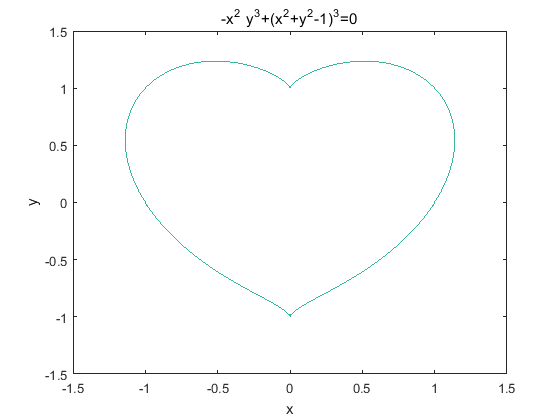
另外一个函数：

ezplot('17*x.^2-16*abs(x).*y+17*y.^2=200'

另外一个分段函数：

   

x=linspace(-2,2,1000);
y1=sqrt(2*sqrt(x.^2)-x.^2);
y2=-2.14*sqrt(sqrt(2)-sqrt(abs(x)));
plot(x,y1,'b',x,y2,'b');
axis([-2.5,2.5,-3,1.5]);

另外一个：

t=linspace(-6,6,1000);
x=16*(sin(t)).^3;
y=13*cos(t)-5*cos(2*t)-2*cos(3*t)-cos(4*t);
plot(x,y);

2. 立体心形图像

立体心形貌似只能由笛卡尔方程得到：

  

画图时用 isosurface 和 patch  函数：

图形1：

f=@(x,y,z)(x.^2+ (9./4).*y.^2 + z.^2 - 1).^3 - x.^2.*z.^3 - (9./80).*y.^2.*z.^3;
[x,y,z]=meshgrid(linspace(-3,3));
val=f(x,y,z);
[p,v]=isosurface(x,y,z,val,0);
patch('faces',p,'vertices',v,'facevertexcdata',jet(size(v,1)),'facecolor','w','edgecolor','flat');
view(3);grid on;axis equal;

图形2：

f=@(x,y,z)(x.^2+ (9./4).*y.^2 + z.^2 - 1).^3 - x.^2.*z.^3 - (9./80).*y.^2.*z.^3;
[x,y,z]=meshgrid(linspace(-1.5,1.5));
val=f(x,y,z);
isosurface(x,y,z,val,0); 
axis equal;view(3);colormap([1 0.2 0.2])

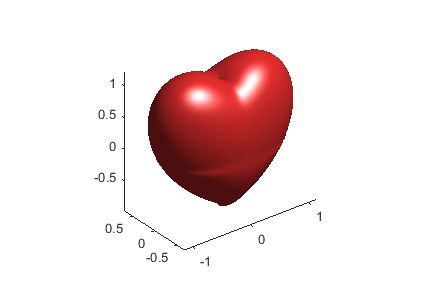
3. 轴对称振荡器函数

    

ezplot('x*sin(x)')

4.  刚好有一个极大点，一个极小点的二元函数

   

    

ezmesh(@(x,y) x.*exp(-x.^2-y.^2))

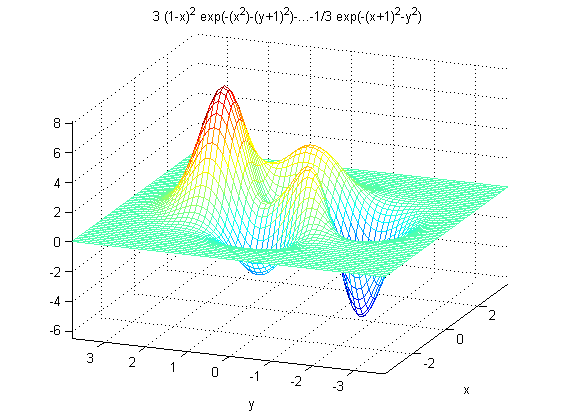
5. peaks 函数（二元高斯分布的概率密度函数）（三个极大点，三个极小点）

   

 f=@(x,y)3*(1-x).^2.*exp(-(x.^2) - (y+1).^2)- 10*(x/5 - x.^3 - y.^5).*exp(-x.^2-y.^2)- 1/3*exp(-(x+1).^2 - y.^2);
 ezmesh(f);