图像缩放算法及速度优化——(二)双线性插值

　　　　双线性插值作为OpenCV中默认使用的图像缩放算法，其效果和速度都是不错的。并且效果也比较稳定，计算复杂度并不算太高。我看了很多网上的算法，自己也没看太懂，下面是从网上找的双线性插值 算法的讲解。
　　　　“图像的双线性插值放大算法中，目标图像中新创造的象素值，是由源图像位置在它附近的2*2区域4个邻近象素的值通过加权平均计算得出的。双线性内插值算法放大后的图像质量较高，不会出现像素值不连续的的情况。然而次算法具有低通滤波器的性质，使高频分量受损，所以可能会使图像轮廓在一定程度上变得模糊。”

　　　　下面还是根据我自己的理解来继续讲述吧，相信读者中有很多高手，希望读者能给予我指点一下，让我也能更明白一些。
　　　　双线性插值 算法和最近邻插值算法比较类似。在最近邻插值算法中，目标图像中的某个点(x,y)是去源图像中找最邻近的一个点(x0, y0)即可。目标图像中的点(x, y)对应于源图像中的点(x0',y0')，x0'、y0'很可能不是整数，而是小数，而最近邻插值算法是找其邻近整型值(int(x0'+0.5f),int(y0'+0.5f))（上篇文章中没有进行四舍五入）。我们现在找x0', y0'所在位置旁边的四个点，根据这四个点与(x0',y0')距离的关系计算目标图像中(x,y)一点的像素值。算法描述如下：

 

(1)计算源图像与目标图像宽与高的比例
w0 : 表示源图像的宽度
h0 : 表示源图像的高度
w1 : 表示目标图像的宽度
h1 : 表示目标图像的高度
float fw = float(w0-1)/(w1-1);
float fh = float(h0-1)/(h1-1);
(2)针对目标图像的一个点(x, y),计算在源图像中的对应坐标，结果为浮点数。
float x0 = x * fw;
float y0 = y * fh;

int x1 = int(x0);
int x2 = x1 + 1;
int y1 = int(y0);
int y2 = y1+1;

所求的源图像中的四个点坐标为(x1, y1) (x1, y2) (x2, y1) (x2,y2)
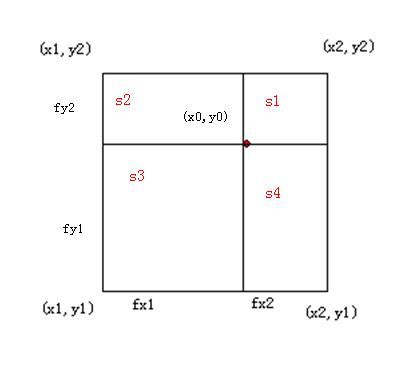
(3)求周围四个点所占的权重比值
如上图，
fx1 = x0 - x1;
fx2 = 1.0f - fx1;
fy1 = y0 - y1;
fy2 = 1.0f - fy1;

float s1 = fx1*fy1;
float s2 = fx2*fy1;
float s3 = fx2*fy2;
float s4 = fx1*fy2;

我们以value(坐标)来代表取得此点的坐标值，则:
value(x0,y0) = value(x2,y2)*s1+value(x1,y2)*s2+value(x1,y1)*s3+value(x2,y1)*s4;

如果 对上述运算不够明白 的话，可以这样来求。
我们先要求得(x0, y1) 和(x0,y2)的像素值。
则float value(x0,y1) = value(x1,y1)*fx2 + value(x2,y1)*fx1;
float value(x0,y2) = value(x1,y2)*fx2 + value(x2,y2)*fx1;
注释：离某点越近，离权重越大，故取其与1的差值。
float value(x0,y0) = value(x0,y1)*fy2 + value(x0,y2)*fy1;
验证后与上边公式一样。
(4)求得值后填充到目标图像上就可以了。

为了能让人更容易理解，咱还是使用GetPixel和SetPixel进行取值和赋值。

 

void ResizeLinear01(CImage& src, CImage& dst)
{
    int w0 = src.GetWidth();
    int h0 = src.GetHeight();
    int pitch0 = src.GetPitch();

    int w1 = dst.GetWidth();
    int h1 = dst.GetHeight();
    int pitch1 = dst.GetPitch();

    float fw = float(w0) / w1;
    float fh = float(h0) / h1;

    int y1,y2, x1,x2, x0,y0;
    float fx1,fx2, fy1, fy2;
    for(int y=0; y<h1; y++)
    {
        y0 = y*fh;
        y1 = int(y0);
        if(y1 == h0-1)    y2 = y1;
        else y2 = y1 + 1;

        fy1 = y1-y0; 
        fy2 = 1.0f - fy1;
        for(int x=0; x<w1; x++)
        {
            x0 = x*fw;
            x1 = int(x0);
            if(x1 == w0-1)    x2 = x1;
            else x2 = x1+1;

            fx1 = y1-y0;
            fx2 = 1.0f - fx1;

            float s1 = fx1*fy1;
            float s2 = fx2*fy1;
            float s3 = fx2*fy2;
            float s4 = fx1*fy2;

            COLORREF c1,c2,c3,c4, color;
            c1 = src.GetPixel(x1,y1);
            c2 = src.GetPixel(x2,y1);
            c3 = src.GetPixel(x1,y2);
            c4 = src.GetPixel(x2,y2);
            BYTE r,g,b;
            r = (BYTE)(GetRValue(c1)*s3) + (BYTE)(GetRValue(c2)*s4) + (BYTE)(GetRValue(c3)*s2) + (BYTE)(GetRValue(c4)*s1);
            g = (BYTE)(GetGValue(c1)*s3) + (BYTE)(GetGValue(c2)*s4) + (BYTE)(GetGValue(c3)*s2) + (BYTE)(GetGValue(c4)*s1);
            b = (BYTE)(GetBValue(c1)*s3) + (BYTE)(GetBValue(c2)*s4) + (BYTE)(GetBValue(c3)*s2) + (BYTE)(GetBValue(c4)*s1);

            dst.SetPixelRGB(x, y, r, g, b);
        }
    }

}

 

测试程序仍是将670*503尺寸的图片缩放为200*160。经过测试，上边的算法执行一次就需要0.5秒左右，可以说是非常的慢。如果将其缩放成2000*1600大小的图片，一次就需要50秒。这是非常可怕的，假如现在我们做一个类似PHOTOSHOP的软件，用户想将其扩大若干倍，却要等50秒，估计用户已经没有耐心使用您的软件了。
我们来分析一下怎样可以优化程序。在每一步优化算法后，我们都再用上边同样的程序和步骤进行测试，观察运行所用时间。
(1)改函数调用 为指针操作如第1节。（进行完此步后，程序只需要0.2秒左右，速度提高了250倍，哈哈！）
(2)将x0,y0坐标的计算提取到 循环外，因为第二层循环里的x坐标每次循环都要重复一次，并且是重复的。（仍然是需要0.2秒左右。我们让其循环一百次，再比较下所用时间。使用ResizeLinear02方法用时19.6秒，使用ResizeLinear02方法都是用时17.4秒，看来还是有作用的。）

下面是最终的代码。

void ResizeLinear04(CImage& src, CImage& dst)
{
    int w0 = src.GetWidth();
    int h0 = src.GetHeight();
    int pitch0 = src.GetPitch();

    int w1 = dst.GetWidth();
    int h1 = dst.GetHeight();
    int pitch1 = dst.GetPitch();

    BYTE* pSrc = (BYTE*)src.GetBits();
    BYTE* pDst = (BYTE*)dst.GetBits();
    BYTE* p0, *p1 = pDst;

    float fw = float(w0-1) / (w1-1);
    float fh = float(h0-1) / (h1-1);

    float x0, y0;
    int y1, y2, x1, x2;
    float fx1, fx2, fy1, fy2;
    
    int* arr_x1 = new int[w1];
    int* arr_x2 = new int[w1];
    float* arr_fx1 = new float[w1];

    for(int x=0; x<w1; x++)
    {
        x0 = x*fw;
        arr_x1[x] = int(x0);
        arr_x2[x] = int(x0+0.5f);
        arr_fx1[x] = x0 - arr_x1[x];
        //TRACE(L"x=%6d; x0=%6.3f; x1=%6d; x2=%6d; fx1=%6.3f;\n", x, x0, arr_x1[x], arr_x2[x], arr_fx1[x]);
    }    
    for(int y=0; y<h1; y++)
    {
        y0 = y*fh;
        y1 = int(y0);
        y2 = int(y0+0.5f);
        fy1 = y0-y1; 
        fy2 = 1.0f - fy1;
        //TRACE(L"y=%6d; y0=%6.3f; y1=%6d; y2=%6d; fy1=%6.3f;\n", y, y0, y1, y2, fy1);
        for(int x=0; x<w1; x++)
        {
            x1 = arr_x1[x];
            x2 = arr_x2[x];
            fx1 = arr_fx1[x];
            fx2 = 1.0f-fx1;

            float s1 = fx2*fy2;
            float s2 = fx1*fy2;
            float s3 = fx1*fy1;
            float s4 = fx2*fy1;
            //TRACE(L"s1=%6.3f; s2=%6.3f; s3=%6.3f; s4=%6.3f; sum=%6.3f\n", s1,s2,s3,s4, s1+s2+s3+s4);
            BYTE* p11 = pSrc + pitch0*y1 + 3*x1;
            BYTE* p12 = pSrc + pitch0*y1 + 3*x2;
            BYTE* p21 = pSrc + pitch0*y2 + 3*x1;
            BYTE* p22 = pSrc + pitch0*y2 + 3*x2;
            
            *p1 = BYTE((*p11)*s1 + (*p12)*s2 + (*p21)*s4 + (*p22)*s3);    p1++;    p11++; p12++; p21++; p22++;
            *p1 = BYTE((*p11)*s1 + (*p12)*s2 + (*p21)*s4 + (*p22)*s3);    p1++;    p11++; p12++; p21++; p22++;
            *p1 = BYTE((*p11)*s1 + (*p12)*s2 + (*p21)*s4 + (*p22)*s3);  p1++;

        }
        p1 = pDst + y*pitch1;
    }

    delete []arr_x1;
    delete []arr_x2;
    delete []arr_fx1;
}