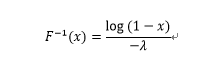C语言下泊松分布以及指数分布随机数生成器实现
最近实验室的项目需要实现模拟文件访问序列,要求单位时间内的数据请求次数符合泊松分布,而两次请求见的时间间隔符合指数分布。没办法只好重新捡起已经丢掉多时的概率知识。于是也就有了这篇关于在C语言下符合泊松分布和指数分布的随机数生成器的实现。
泊松分布
在实际的事例中,当某一事件,比如进站乘客数量,电话交换机接收到的通话请求以固定的瞬时速率λ独立且随机地出现时,就可以认为该事件在单位时间内发生的次数符合泊松分布。
首先必须由二项分布引出:
如果做一件事情成功的概率是 p 的话,那么独立尝试做这件事情 n 次,成功次数的分布就符合二项分布。展开来说,在做的 n 次中,成功次数有可能是 0 次、1 次 …… n次。成功 i 次的概率是:
( n 中选出 i 项的组合数) * p ^ i * (1-p)^ (n-i)
以上公式很容易推导,用一点概率学最基本的知识就够了。因为每一特定事件成功的概率是 p ,不成功的概率是 1-p 。i 次成功的事件可以任意分布在总共的 n 次尝试中。把它们乘起来就是恰好成功 i 次的概率。
当我们把二项分布推而广之后,就可以得到波松分布。
可以这样考虑,在一个特定时间内,某件事情会在任意时刻随机发生(前提是,每次发生都是独立的,且跟时间无关)。当我们把这个时间段分成非常小的时间片构成时,可以认为,每个时间片内,该事件可能发生,也可能不发生。几乎可以不考虑发生多于一次的情况(因为时间片可被分的足够小)。
当时间片分的越小,该时间片内发生这个事件的概率 p 就会成正比的减少。即:特定时间段被分成的时间片数量 n 与每个时间片内事件发生的概率 p 的乘积 n*p 为一个常数。这个常数表示了该事件在指定时间段发生的频度。
回过头来再来看这段时间内,指定事件恰好发生 i 次的概率是多少?代入上面推导出来的公式得到:
n * (n-1)... (n-i+1) / i! * p^i * (1-p) ^ (n-i) => np(np-p)...(np-ip+p) / i! * ((1-p) ^ (-1/p))^(-np) / (1-p) ^i
当 n 趋向无穷大时,p 趋向 0 。而此时 (1-p)^(-1/p) 趋向 e 。
上面这个公式可以划简为
其中λ 事件发生的平均速率。
有了这些知识,那么写出符合泊松分布的随机数生成器程序也就不难了:
int possion(int Lambda)
{
int k = 0;
long double p = 1.0;
long double l = exp(-Lambda);
srand((unsigned)time(NULL));
//printf("%1.5Lf\n", l);
while(p>=l)
{
double u = U_Random();
p *= u;
k++;
}
return k-1;
}
double U_Random()
{
double f;
f = (float)(rand() %100);
return f/100;
}
指数分布
指数分布是一种连续的概率分布,通常可以用来描述连续的独立随机事件发生的时间间隔。其概率密度函数为:
其中λ是事件发生的平均速率。
对于较为简单的概率分布,其随机数生成器可以通过其对应的累积分布函数的逆函数构造。具体的证明可以参考这篇文章:点击打开链接。对于指数分布来说,其累积分布函数为:
那么其逆函数则为:
所以其随机数生成器程序为:
double randomExponential(double lambda)
{
double pv = 0.0;
pv = (double)(rand()%100)/100;
while(pv == 0)
{
pv = (double)(rand() % 100)/100;
}
pv = (-1 / lambda)*log(1-pv);
return pv;
}