Real-Time Rendering-附录A 线性代数

Appendix A Some Linear Algebra（附录A 部分线性代数知识）

A point is that which has no part.
A line is a breadthless length.
The extremities of a line are points.
A straight line is a line which lies evenly with the points on itself.*
—The first four definitions from Elements by Euclid [320]

本部分内容主要讲解计算机图形学中大量使用的线性代数的基本概念。我们讲述的方式不会像一般的线性代数书籍那样描述一些抽象的数学，而是重点关注与计算机图形学最相关的内容。对于那么没有深入学习线性代数的读者，这部分内容可以作为一个简单的介绍，而对于已经完全掌握线性代数的读者，也可以作为复习。

在第一节我们将会介绍欧几里得空间。一开始可能会觉得很抽象，但是在该节之后，我们会讨论与之关联的几何应用，向量基和矩阵概念。因此咬牙坚持学完第一节的内容，在附录的其他章节以及本书的大部分章节中你将到收获更多的回报。

如果你对本书中使用的数学记号不太熟悉，请查看第一章1.2节。

A.1 Euclidean Space（欧几里得空间）

表示 n 维实时的欧几里得空间的记号为 Rn 。在该空间中，向量 v 是一个 n 元组，即一个实数的有序列表：

v∈Rn⟺v=⎛⎝⎜⎜⎜⎜v0v1⋮vn−1⎞⎠⎟⎟⎟⎟with vi∈R, i=0,⋯,n−1(A.1)

注：该有序列表的下标从 0 开始，到 n−1 结束，这种编号方式与大部分编程语言，如C和C++的数组索引下标相同。因此可以简单的把公式转换成代码。在某些计算机图形和线性代数书籍中该下标值从 1 到 n 。

该向量也可以使用一种行向量的形式表示，但是大多数计算图形书籍中都是使用列向量，称为列主向量形式。我们可以把 v0,…,vn−1 称为向量 v 的元素，系数或分量。所有小写粗体字母表示位于 Rn 空间的向量，而小写斜体字母表示 R 空间的标量。例如，一个二维的向量可以表示为 v=(v0,v1)T∈R2 。位于欧几里得空间的向量可以执行两种运算，加法和标量乘法，这两种运算过程与我们预期的一样，分别对应于公式A.2和A.3：

u+v=⎛⎝⎜⎜⎜⎜u0u1⋮un−1⎞⎠⎟⎟⎟⎟+⎛⎝⎜⎜⎜⎜v0v1⋮vn−1⎞⎠⎟⎟⎟⎟=⎛⎝⎜⎜⎜⎜u0+v0u1+v1⋮un−1+vn−1⎞⎠⎟⎟⎟⎟∈R(加法)(A.2)

和

au=⎛⎝⎜⎜⎜⎜au0au1⋮aun−1⎞⎠⎟⎟⎟⎟∈R(标量乘法)(A.3)

其中记号“ ∈R ”表示执行加法和标量乘法运算的向量位于同一个空间中。从上面的公式中可以看出，向量加法是对逐个分量相加，向量与标量的乘法是对向量的每一个元素与标量 a 相乘。

欧几里得空间运算具有一系列的定律。在欧几里得空间的向量加法运算与预期的一样，具有交换律和结合律：

注：实际上这些定律就是欧几里得空间的定义。

(i)(ii)(u+v)+w=u+(v+w)u+v=v+u(结合律)(交换律)(A.4)

在欧几里得空间中有一个唯一的向量称为零向量， 0=(0,0,⋯,0) ，向量中每一个元素都为0，并具有如下的性质：

(iii)0+v=v(zero identity)(A.5)

另外还有一个相反向量 −v=(−v0,−v1,…,−vn−1) ，具有如下性质：

(iv)v+(−v)=0(加法逆元)(A.6)

向量与标量的乘法运算具有以下性质定律：

(i)(ii)(iii)(iv)(ab)u=a(bu)(a+b)u=au+bua(u+v)=au+av1u=u(分配律)(分配律)(A.7)

在欧几里得空间中，我们可能还会计算两个向量 u 和 v 的点积。点积的表示为 u⋅v ，定义如下：

注：点积也称为内积或标量积

(iv)u⋅v=∑i=0n−1uivi(点积)(A.8)

点积具有如下性质定律：

(i)(ii)(iii)(iv)(v)u⋅u≥0，当且仅当u=(0,0,⋯,0)=0时，才有u⋅u=0(u+v)⋅w=u⋅w+v⋅w(au)⋅v=a(u⋅v)u⋅v=v⋅uu⋅v=0⟺u⊥v.(A.9)

点积的最后一个定理公式表示，如果两个向量的点积为0，那么这两个向量互相垂直（正交）。一个向量范数可以表示为记号 ∥u∥ ，这是一个非负数值，可以使用以下的点积表达式运算得到：

∥u∥=u⋅u−−−−√=(∑n−1i=0u2i)−−−−−−−−√(向量范数)(A.10)

向量范数具有如下性质定律：

(i)(ii)(iii)(iv)∥u∥=0⟺u=(0,0,⋯,0)=0∥au∥=|a| ∥u∥∥u+v∥≤∥u∥+∥v∥∥u⋅v∥≤∥u∥ ∥v∥(三角不等式)(柯西不等式)(A.11)

在下一节，我们开始讨论本节的理论在几何中的具体意义。

A.2 Geometrical Interpretation（几何意义）

这一节，我们开始讲解向量（上一节）的几何意义。首先，我们需要介绍向量的线性无关和向量基的概念。

注：线性无关和向量基的概念与任何几何空间无关。

如下所示：

v0u0+⋯+vn−1un−1(A.12)

只有在所有标量 v0=v1=⋯=vn−1=0 的情况下，公式A.12才成立，我们就称向量 u0,⋯,un−1 是线性无关的。否则就称为线性相关。

例如，向量 u0=(4,3) 和 u1=(8,6) 是线性相关的，因为在 v0=2 和 v1=−1 的情况下公式A.12成立。只有相互平行的向量才是线性相关的。

如果一组向量 u0,⋯,un1∈Rn 是线性无关的，并且任意的向量 v∈Rn 可以表示为

v=∑i=0n−1viui(A.13)

那么就称向量 u0,⋯,un1 构成欧几里得空间 Rn 。此外，如果对于所有的 v∈Rn ，向量 v 可以确定唯一的 v0,⋯,vn−1 ，就称向量组 u0,⋯,un1 为 Rn 的向量基。意思是 Rn 中的每一个向量都可以由 n 个标量 (v0,v1,⋯,vn−1) 和向量基 u0,⋯,un1 唯一确定。我们把空间中线性无关的最大向量个数称为空间的维数。

例如，向量 u0=(4,3) 和 u1=(2,6) 构成了一个线性无关基。在这个二维空间 R2 中，任何向量都可以由这两个向量唯一的组合表示。比如，向量 (−5,−6) 可以由 v0=−1 和 v1=−0.5 描述，并且只有这一种组合方式。

要完整定义一个向量 v ，我们需要使用公式A.13，即要同时使用向量的分量 vi 和向量基 ui 。但是这种方法通常是不实用的，因此在所有的向量都使用相同的基向量时可以在数学操作中操作基向量。在这种情况下，向量 v 可以描述为：

v=⎛⎝⎜⎜⎜⎜v0v1⋮vn−1⎞⎠⎟⎟⎟⎟,(A.14)

这种描述方法与公式A.1完全一样，因此这是A.1节的向量与本节所讨论的几何向量的一一映射。

注：这种映射方式在数学中称为同构

如图A.1所示，阐述了一个三维向量对应的几何形式。

图A.1 使用 R3 中的向量基 u0,u1,u2 表示的一个三维向量 v=(v0,v1,v2) 。注意这是一个右手坐标系。

一个向量 v 可以代表一个坐标点，或一个带有方向的线段（限方向向量）。在A.1节向量的所有定律在几何向量中同样适用。例如，公式A.2中的加法和标量乘法运算如图A.2所示。另外，一组基向量也具有不同的“左右手坐标系”。使用右手系表示一个三维的基向量， x 轴沿着拇指方向， y 轴沿着食指方向，而 z 轴则沿着中指方向。如果使用左手进行笔划，就会得到一个左手系基向量。请查阅901页了解更多左右手系的定义形式。

图A.2 左边两幅图中显示了向量与向量的加法运算。这种方法称为三角形法则（head-to-tail定理）和平行四边形法则。最右边的两幅图分别表示使用一个正值 a 和一个负值 −a 执行标量-向量乘法运算。

一个向量的范数（见公式A.10）可以看成是向量的长度。比如，一个二维向量 u 的长度为 ∥u∥=u20+u21−−−−−−√ ，这是基于Pythagorean theorem（毕达哥拉斯定理）。要创建一个单位向量，即向量长度为1，需要对向量执行规范化。这是通过除以向量的长度进行计算的： q=1∥p∥p ，其中 q 就是规范化向量，也称为单位向量。

对于 R2 和 R3 ，二维和三维向量空间，也可以使用以下的公式表示点积，这与公式A.8相等：

u⋅v=∥u∥ ∥v∥cosϕ(A.15)

其中， ϕ （如图A.3的左图所示）是向量 u 和向量 v 的最小夹角值。我们假设这两个向量都为非零向量，那么由向量点积运算的结果符号可以得到以下结论。1) u⋅v=0⟺u⊥v ，即如果向量 u 和向量 v 的点积为0，那么这两个向量相互正交（垂直）。2)如果 u⋅v>0 ，表示 0≤ϕ<π2 ，同理，如果 u⋅v<0 ，则表示 π2≤ϕ<π 。

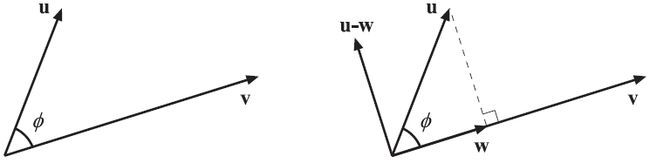
图A.3 左图中显示了几何向量的点积运算的符号。右图中显示了正交投影的几何表示，其中向量 u 正交（垂直）投影到向量 v ，产生了向量 w 。

现在我们再回过头来讨论向量基，并介绍一种特殊的标准正交基。对于标准正交基，组成该基的向量组 u0,⋯,un−1 必须要具有如下性质：

ui⋅uj={0,1,i≠j,i=j,(A.16)

这意味着每一个基向量的长度必须为1，即 ∥ui∥=1 ，并且每一对基向量必须是相互正交的，即这一对向量的夹角为 π/2 弧度（ 90∘ ）。在本书中，我们大部分情况下都使用二维或三维标准正交基。如果基向量组互相垂直，但向量长度不是单位长度，则称该向量基为正交基。标准正交基不一定要全部由简单向量组成。例如，precomputed radiance transfer（PRT，全局光照）技术所使用的标准正交基可以是球谐函数或小波函数。通常情况下，基向量组被用于交换这些函数，向量的点积用于补充函数。一旦完成这两点，标准正交基的概念就可以用于计算这两个函数。关于这方面的详细讲解，请查看8.6.1节。

设向量 p=(p0,⋯,pn−1) ，那么对于标准正交基的情况还可以表示为 pi=p⋅ui 。意思是，如果有一个向量$mathbf{p}和一个基（基向量组分别为 u0,⋯,un−1 ），那么通过把向量$mathbf{p}与每一个基向量简单地执行点积运算，就可以得到该向量的每一个元素值。最常用的向量基是标准基，其中基向量表示为 ei 。第 i 个基向量除了第 i 个位置的元素值为1外其他的元素值全为0。对于三维的标准基，对应的基向量分别为 e=(1,0,0)，e1=(0,1,0)，e2=(0,0,1) 。另外，我们还可以把这三个向量表示为 ex，ey，ez ，这就是我们平常所用的 x，y 和 z$ 轴。

点积运算的一个非常有用的特点是计算一个向量在另一个向量上的正交投影。如图A.3所示，右图中向量 u 在向量 v 上的正交投影（向量）为 w 。

对于任意的向量 u 和向量 v ，可以使用如下公式计算向量 w ：

w=(u⋅v∥v∥2)v=(u⋅vu⋅v)v=tv(A.17)

其中 t 是一个标量。希望读者能自行检验并使用公式A.15验证公式A.17的正确性。另外，正交投影还可以得到向量 u 的正交分量，分为向量 w 和 (u−w) 两部分。从中可以看出 w⊥(u−w) ，以及 u=w+(u−w) 。此外，还可以得出结论，如果向量 v 已经被规范化，那么投影向量 w=(u⋅v)v 。意味着 ∥w∥=|u⋅v| ，即向量 u 和 v 的点积的绝对值就是向量 w 的长度。

Cross Product（叉积）

叉积也称为向量积，叉积与前面介绍的点积是向量中的两个非常重要的运算操作。

在 R3 中，向量 u 和向量 u 的叉积可以使用一个唯一的向量 w 表示为 w=u×v ，并具有以下性质：

• ∥w∥=∥u×v∥=∥u∥ ∥v∥sinϕ ，与之前一样， ϕ 也是向量 u 和向量 v 的最小夹角值。如图A.4所示。
• w⊥u 并且 w⊥v 。
• u，v，w 形成了一个右手坐标系。

图A.4 向量叉积的几何表示。

从该定义中可以得出，当且仅当 u∥v （即向量 u 与向量 v 平行）时， u×v=0 ，此时 sinϕ=0 。与其他运算操作一样，点积运算也具有以下运算律：

(i)(ii)(iii)(iv)u×v=−v×u(au+bv)×w=a(u×w)+b(v×w)(u×v)⋅w=   (w×u)⋅v=−(u×w)⋅v=   (v×w)⋅u=−(v×u)⋅w=−(w×v)⋅u⎫⎭⎬⎪⎪u×(v×w)=(u×w)v−(u×v)w(反交换律)(线性关系)(标量三重积)(向量三重积)(A.18)

从这些定律中可以明显得出结论，要从计算中得到正确的结果操作数据顺序是到头重要的。
对于一个标准正交基中的三维向量 u 和向量 v ，根据公式A.19计算它们的叉积：

w=⎛⎝⎜wxwywz⎞⎠⎟=u×v=⎛⎝⎜uyvz−uzvyuzvx−uxvzuxvy−uzvy⎞⎠⎟.(A.19)

我们可以使用一种非常容易记忆的称为Sarrus’s scheme的方法，推导出公式A.19，推导过程如下所示：

+  +  +−  −  −↘ ↘ ↘↙ ↙ ↙ex  ey  ez  ex  ey  ezux  uy  uz  ux  uy  uzvx  vy  vz  vx  vy  vz(A.20)

对于该结构图中的每一个箭头，把沿着对角线箭头方向的全部元素相乘生成其中一项，并指定与箭头对应的符号为该乘积的符号。计算的结果如下所示，正如预期一样，这种计算方法与公式A.19完全相同：

u×v= +ex(uyvz)+ey(uzvx)+ez(uxvy)−ex(uzvy)−ey(uxvz)−ez(uyvz).