机器学习教程 之 梯度提升方法:GBDT及其扩展模型XGBoost
Gradient boosting是一种广泛被用于回归、分类和排序任务的集成方法,于2001年被Friedman提出
该类算法通过以上一轮基学习器的误差的负梯度为训练目标训练本轮的基学习器,不断降低集成模型在训练集上的偏差实现高精度的集成
基于Gradient Boosting算法的学习器被称为Gradient Boosting Machine(GBM),如果说AdaBoost是boosting方法的开山之作,那么GBM就是boosting方法的集大成者。GBM几乎刷新了各个领域众多数据集的精度记录,有人认为GBM是性能最好的机器学习方法,这种说法有点激进,但通常各类数据竞赛赢家的策略里也确实都会有这类算法的方法或者思想
由于集成学习方法在实际应用中出色的性能,我曾经写过几篇这方面的博文,关于集成学习及其boosting方法的
机器学习教程 之 Boosting 与 bagging:集成学习框架
人工智能里的数学修炼 | AdaBoost的数学原理: 分布更新推导
机器学习教程 之 集成学习算法: 深入刨析AdaBoost
还有一片关于 bagging 类随机森林的
机器学习教程 之 随机森林: 算法及其特征选择原理
感兴趣的朋友可以了解一下,可以帮助你们更好的了解集成学习的整体情况
其实很早就打算着手写GBDT还有XGBoost,但是之前一直感觉还不太能驾驭,所以一直没有动手,这次借着课题组报告的机会花了一个星期把GBDT的大纲整理了一下做成了ppt,这篇文章是对ppt的解释和扩充,算是给自己的一个总结和交待。
ppt在这里,想要看精简版的可以了解一下
Gradient Boost Decision Tree(GBDT)及其拓展模型
这篇文章主要分为三个部分:
第一部分 以GBDT的回归模型来详细讲解模型的原理和算法
第二部分 讲解GBDT的扩展实现:XGBoost
第三部分 这里会介绍一下xgboost库以及常用的GBDT类模型库的调参方法
一、GBDT的回归模型
GBDT可以用于回归、分类、排序等各种任务,这里以回归模型为例进行讲解是因为GBDT在回归问题上可解释性是最强的,分类及排序等模型只需要在回归原理上稍做修改即可。关于GBDT的理解主要有一下几个比较重要的点
1. GBDT的基分类器为CART树(分类回归树)
2. 一种boosting方法:Boosting Tree 提升树
3. 加性模型与前向分布算法
4. Gradient Boosting 梯度提升
5. GBDT采用的一些小技巧
接下来我会从这五个方面,一步一步的把GBDT说清楚
1.1 GBDT的基分类器:CART树
CART树的全称是分类回归树,这是一种二叉树,可以处理分类与回归两种问题,是Breiman于1984年提出的一种树模型,后来他还基于这种方法提出了著名的随机森林。
CART树可以处理分类与回归两种问题,处理两类问题的策略不同,但分类树与回归树的生成框架是相同的,唯一不同的地方在于节点的属性选择标准。分类树采用的选择标准是Gini系数,认为Gini系数小的属性比较好,回归树采用最小二乘计算每个属性的划分误差,认为划分误差小的属性比较好
分类树与普通的决策树计算并没有什么不同,这里主要讲一下最小二乘回归树的具体计算方法,回归树主要有以下几点:
1.回归树在每个划分节点都会得到一个预测值,以标签是身高为例,这个预测值就是这个节点上所有样本身高的平均值

2.分枝时遍历所有的属性进行二叉划分,挑选使平方误差最小的划分属性作为本节点的划分属性
3.遍历每个属性找到使loss最小的属性,令其为当前节点的属性
第t个属性的平方误差计算公式为
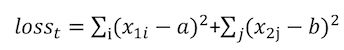
4.如果属性有多种可能取值,需要遍历所有可能的切分点,找到使loss最小的切分点作为该属性的二叉划分点
5.对子集继续选择性的最优特征进行划分,直到每个叶子节点仅有一个样本(这种情况是很少见或者难以实现的,通常会设定 一个允许叶子节点保留最少样本数的参数,满足条件即可停止,如果叶子节点有多个样本值,以均值作为该叶子节点的预测值)
以上就是回归树相比于分类树需要注意的地方
补充:为什么集成算法大多使用树类模型作为基学习器?或者说为什么集成学习可以在树类模型上取得成功?
树模型具有很多优良的性质,比如预测速度快、不需要进行特征标准化、可解释性强等优点,
但是单独使用决策树会有树节点过深导致的过拟合等问题
而集成学习的bagging和boosting两类主流算法:
bagging,关注于提升分类器的泛化能力,比如随机森林就通过对样本和特征进行采样训练
基分类器来增强其整体对样本变化的适应能力, 所以在随机森林里对于树的max_depth这个
参数一般不会加以限制,bagging本身就是一种避免过拟合的方法
Boosting, 关注于提升分类器在训练集上的精度,这似乎是一种容易过拟合的方法,但是
Boosting在设计时会有很多避免过拟合的技巧,比如设置max_depth,限制树的最大深度、
限制叶子节点的最少样本数量等方法避免过拟合,这些限制可能会降低单个树的精度,但boosting
可以将集成的精度问题交给其为精度提升而设计的框架去解决
所以不论是bagging还是boosting类的方法都可以做到单独的决策树无法做到的方面,从
而实现性能的提升
1.2 Boosting Tree 提升树方法
简单来说,Boosting Tree方法通过以上一轮基学习器的误差为训练目标训练本轮的基学习器,不断降低集成模型在训练集上的偏差实现高精度的集成
举个例子:对于回归问题,如果我们预测的标签值是20

按照如上的图例,第三次的预测标签为 20-13-8 = -1 ,不断重复这个过程,直到生成指定数量的基分类最后将所有预测结果相加即为集成模型的预测结果
1.3 加性模型与前向分步算法
Boosting方法大多采用加性模型来组合弱学习器,即可以将集成的学习器表示为如下形式:

这里 hm h m 表示第 m m 个基学习器, βm β m 表示第 m m 个基学习器的系数, am a m 表示第 m m 个基学习器的参数, M M 表示基学习器的个数
对于刚刚提到的Boosting Tree方法,基学习器的系数 βm β m 为1, 将加性模型简写为

在给定损失函数 L L 以及训练数据的条件下,学习加性模型 H(x) H ( x ) 就是一个搜寻参数 α α 使得损失函数极小化的过程,即
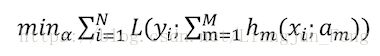
直接求解这个极小值是个很复杂的优化问题,我们采用前向分步算法来简化这一问题。前向分步算法本质上是一种贪心算法,它通过每一步只学习一个基函数及其系数,逐步逼近优化目标来简化复杂度
首先,我们来重写一下加性模型的表达形式,共生成 M M 个基分类器,当前迭代次数为 m m ,即在第 m m 个循环中,Boosting Tree的加性模型可以写为

前向分步算法只要求在第 m m 轮时,优化当前轮次的基学习器的参数,使得损失函数最小以简化算法,即
这里优化当前轮次的基学习器的参数,在经典的GBDT算法中,采取的是非常暴力的遍历的方式, 即在每个节点划分的时候,遍历所有属性和可能的节点划分数值,在当前指定的损失函数下使损失达到最小,这点在之前提回归树的时候提到了
当我们采用平方损失函数,即
我们有
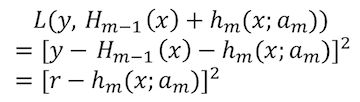
这里的 r=y−Hm−1(x) r = y − H m − 1 ( x ) ,即上一轮基学习器训练完成以后, m−1 m − 1 个基学习器与标签的残差,所以,对于回归问题的Boosting Tree 来说,每一步只需要拟合当前模型的残差就可以了。这里得强调一下,Boosting Tree拟合的残差是在平方损失函数的前提下优化出来的结果,换了别了损失函数拟合的可能就不是残差了
1.4 Gradient Boosting 梯度提升
Gradient Boosting 是GBDT的核心思想,它相比与 Boosting Tree 的主要改进在于:
Boosting Tree 对于每一轮基学习器,拟合的是当前模型与标签值的残差
GBDT 对于每一轮基学习器,拟合的是当前模型与标签值的残差的负梯度
这里会有一些问题:
1. 什么是残差的负梯度?
2. 为什么拟和残差的负梯度可以降低集成模型的损失,即为什么拟合残差的负梯度是可行的?
3. 即便拟合残差的负梯度是可行的,为什么不直接拟合残差?拟合残差的负梯度好在哪里?
这几个问题的难度是一次增加的,接下来我们一个一个来回答
1.4.1 什么是残差的负梯度?
对于 i=1,2,3…,N i = 1 , 2 , 3 … , N 个样本,每一个样本的残差负梯度的计算公式为:
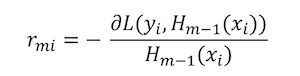
看公式可能不太清楚,举个例子:
对于平方损失函数 L(y,H(x))=1/2(y−H(x))2 L ( y , H ( x ) ) = 1 / 2 ( y − H ( x ) ) 2 ,其残差的负梯度为 y−H(x) y − H ( x )
可以发现, 当损失为平方损失函数时,GBDT 和Boosting Tree的拟合对象是一致的,但这只是一个特例,GBDT对于回归问题常用的损失函数,及负梯度如下

1.4.2 拟合残差的负梯度为什么是可行的?
拟合残差的负梯度是可以用泰勒展开来解释的, 泰勒一阶展开式:
加性模型在第 m m 轮可以写为 Hm=Hm−1+hm H m = H m − 1 + h m
对 L(y,Hm−1+hm) L ( y , H m − 1 + h m ) 作一阶泰勒展开可以有:
其中

即 m−1 m − 1 轮残差的梯度
加性模型在第 m m 轮和 m−1 m − 1 轮的损失分别为:
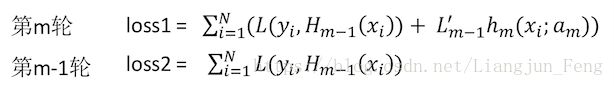
我们希望每一轮性的基学习器之后损失都是下降的,即 loss1<loss2 l o s s 1 < l o s s 2 , 那么比较上面两个式子,我们可以发现,损失能否下降,关键在于 Key=L′m−1hm(xi;αm) K e y = L m − 1 ′ h m ( x i ; α m ) 项的正负如何
很简单的,我们只需要令 hm(xi;αm)=−L′m−1 h m ( x i ; α m ) = − L m − 1 ′ ,则
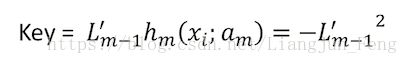
该项便会恒为负,即损失会向着下降的方向移动,这其实也是梯度下降的思想。这里令 hm(xi;αm)=−L′m−1 h m ( x i ; α m ) = − L m − 1 ′ 也就是令第 m m 个学习器拟合当前模型残差的负梯度
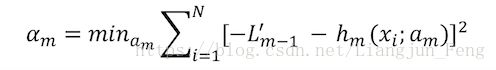
在之前的boosting Tree还有残差负梯度的推导中,我们已经说明了 hm(xi;αm) h m ( x i ; α m ) 的拟合对象和参数 αm α m 的搜索方法(遍历)。这里再具体说一下每一棵树对于残差负梯度的拟合
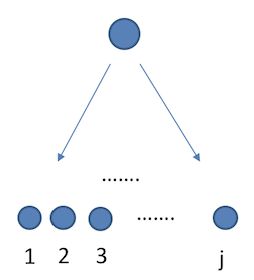
第 m m 个回归树的叶子节点的值 βm β m 都是一个向量, j j 为第 m m 个回归树的叶子节点个数,需要注意的是,我们每棵树拟合的对象是残差的负梯度,但是一棵树的每个叶子节点里往往不仅仅只有一个样本,而这些样本又会有不同的标签值,那么每个叶子节点的值是怎样确定的呢?我们之前说回归树是采用取平均的方法,而GBDT没有采用这种方式,而是采用了线性搜索一个参数来进行的优化。

即以每一个叶子节点为单元进行优化, 这里的 bmj b m j 表示是叶子节点的输出值, ρmj ρ m j 表示的是以损失函数最低为目标进行线性搜索得到的值,所以,每课树在训练完成之后,其叶子节点的输出值,是要经过一个 ρmj ρ m j 的更新的,对于一些特殊的情况Fredman在论文中给出了 ρmj ρ m j 的估计式子,从而避免了线性搜索的计算量,关于这部分,我会具体的在下一篇关于GBDT的博文中进行展开的讲解,上面的式子可以写为
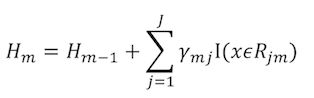
到目前为止我们已经讨论了GBDT的主要原理,包括:每一个基学习器的拟合目标是什么?为什么对负梯度进行拟合是可行的?每个基学习器的参数 αm α m , ρmj ρ m j 是怎样得到的?
1.4.3为什么GBDT要以残差的负梯度替代Boosting Tree的残差作为基学习器的学习目标?
这是问的最多的一个问题,也是很难回答的一个问题。Boosting Tree 和 GBDT 两者的相同之处在于,都是迭代回归树,都是累加每棵树的结果作为最终结果,每棵树都在学习前m-1棵树尚存的不足,从总体流程和输入输出上两者是没有区别的
两者的主要区别就在于每步迭代的时候是否使用残差的负梯度作为树的拟合对象,前者不用残差的负梯度而是使用残差,是全局最优值,后者使用的是 局部最优方向(负梯度)*步长( β β ),即前者是每一步都试图让结果变成最好,后者则每步试图让结果更好一点
Boosting Tree的最大问题在于,它依赖残差进行优化,损失函数一般固定为反应残差的均方差损失函数,因此当均方差损失函数失效(该损失函数对异常值敏感)的时候,换了其他一般的损失函数,便很难得到优化的结果。同时,因为损失函数的问题,它也很难处理回归之外问题。 而后者使用梯度下降的方法,对于任意可以求导的损失函数它都可以处理
GBDT本质上是以梯度下降的办法简化了Boosting Tree对于损失函数的优化求解问题
1.5 GBDT 里用到的一些技巧
除了以上说明的梯度提升办法,GBDT还采用了很多使用技巧,之所以说他们是技巧,是因为这些方法在实际中取得成功,却很难在理论上证明
1.5.1 Shrinkage 收缩
Shrinkage的思想认为,每次走一小步逐渐逼近结果的效果,要比每次迈一大步很快逼近结果的方式更容易得到精确值,即它不完全信任每一棵残差树,认为每棵树只学到了真理的一部分累加的时候只累加了一小部分多学几棵树来弥补不足。 这个技巧类似于梯度下降里的学习率
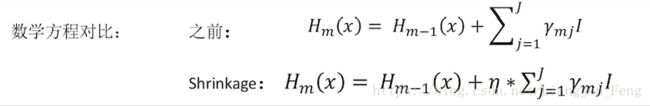
学习率 是一个人为设置的参数,用来调整学习的快慢和精度, 学习率一般取0.001到0.01,设置的越小,需要训练的回归树越多。

1.5.1 重复使用属性
在GBDT的每一棵回归树中,一个属性可以在多个节点用用到,更准确的说,这是CART树本身具有的性质,CART每一个节点都是遍历每一个属性和划分点得来的,即便是同一个属性也有可能因为不同的划分点带来不同的划分效果
1.5.2样本采样
GBDT学习了随机森林里的样本采样方法,每一棵树基于原始样本的一个子集进行训练达到防止过拟合和提升训练速度的目的
到这里为止,我们就讲完了GBDT回归模型的全部内容
二、GBDT的最强实现 Extreme Gradient Boosting (XGBoost)
XGBoost是华盛顿大学的陈天奇博士于2014年开源的一个GBDT库,论文发于2016年,它在算法层面和实现层面较以往的GBDT有很大改进,在实践中,精度有很大的提升同时,计算速度较传统的GBDT实现也快了近10倍量级
XGBoost在算法层面相比于GBDT做出的改进主要有以下几点:
2.1 显式的将树模型的复杂度作为正则项加在优化目标里
数学模型的修改:
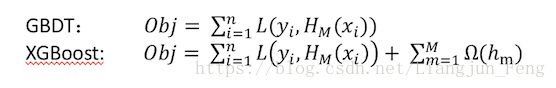
上式中 M M 代表基分类器的个数, Ω(hm) Ω ( h m ) 代表第 m m 棵树模型的复杂度
那么,XGBoost是具体以怎样方式来描述树模型的复杂度的?
首先,我们将一棵回归树的定义做一下细化,将一棵树拆分为结构部分 q q 和叶子权重部分 w w :
上式中 q q 代表从输入到输出的映射结构, w w 是一个向量,向量的元素是每个叶子节点的值。( xϵRl,q:Rl−>T,wϵRT x ϵ R l , q : R l − > T , w ϵ R T ,这里的T代表叶子节点的数量,下图中的T为3)

每一棵树的正则项 Ω(hm) Ω ( h m ) 由两部分组成:
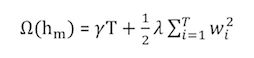
2.2 GBDT用了泰勒展开的一阶导数信息,XGBoost将它扩展到了二阶信息
XGBoost的损失函数:

根据前向分布算法,在第m轮优化的目标就是
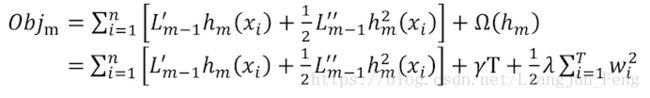
将每棵树拆分成叶子节点,即将 h h 用 w w 表示,可将上式重写为
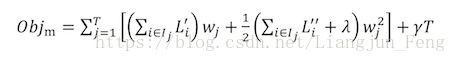
当树的结构q确定时,我们可以通过调整 wj w j 即叶子节点的输出降低损失,对上式求导取0,可以得到优化值:

上面这个式子可以理解为对树的结构 q q 的一个打分函数,损失越小,结构 q q 越好,不过我们不太可能在计算时枚举所有的树结构,一般采用的是贪心算法。即每一次尝试去对已有的叶子加入一个分割。对于一个具体的分割方案,我们获得的增益可由下式计算
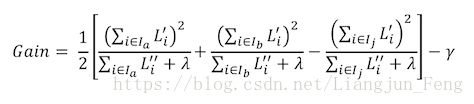
上式中 a,b a , b 代表新分裂的子节点, j j 代表母节点,上式代表产生的两个新的子节点损失之和与原先一个母节点的损失的差值的负值,该值越大,增益越大。
2.3 GBDT在XGBoost样本采样的基础上,增加了属性采样防止过拟合
GBDT模仿了随机森林的横竖采样,用以加速计算和防止过拟合
除了上述几点算法层面的改进,XGBoost相比于GBDT在具体实现上还有一些其他的设计用以加速运行
三、XGBoost参数讲解
XGBoost作为一个集成的分类器,有着大约20个可调参数,但其中主要的也就一手之数,理解这些参数的意义可以更好的帮助我们理解和使用它,下面是xgboost的主要参数
class XGBRegressor(XGBModel, sklearn.base.RegressorMixin)
| Parameters |
|---|
| max_depth : int 表示基分类器的最大深度 一般取3~6 |
| learning_rate : float 学习率,一般取0.001~0.1 |
| n_estimators : int 训练的基分类器个数,默认100个 |
| min_child_weight : int 叶子节点里样本预测值的最小和,用来防止过拟合,默认为1 |
| subsample : float 样本采样比例 |
| colsample_bytree : float 属性采样比例 |
| reg_alpha : float (xgb’s alpha) L1 正则项的系数 |
| reg_lambda : float (xgb’s lambda) L2正则项的系数 |
关于XGBoost和GBDT的调参方法,我还有另一篇博客讲述了具体的方法
机器学习教程 之 参数搜索:GridSearchCV 与 RandomizedSearchCV || 以阿里IJCAI广告推荐数据集与XGBoostClassifier分类器为例
参考文献
[1] Chen T, Guestrin C. XGBoost: A Scalable Tree Boosting System[J]. 2016:785-794.
[2] Library W P. Classification and regression tree[J].
[3] Friedman J, Hastie T, Tibshirani R. Additive logistic regression: a statistical view of boosting (With discussion and a rejoinder by the authors)[J]. Annals of Statistics, 2000, 28(2):337-374.
[4] Friedman J H. Greedy Function Approximation: A Gradient Boosting Machine[J]. Annals of Statistics, 2001, 29(5):1189-1232.