个人机器学习笔记之SVM

吴恩达机器学习笔记（4）——SVM

机器学习个人笔记，学习中水平有限，内容如有缺漏还请多多包涵。

序言

本来打算接着按视频顺序学习神经网络的，但是考虑到神经网络是一个很大块的知识点，于是打算先学完监督学习部分中小块的知识再来攻坚，可没想到SVM这章并没有给出实现的公式，因此只好调用现成的库（主要是sklearn）来完成SVM的探究。

调用sklearn实现的SVM的python代码

import numpy as np
from sklearn import svm
import matplotlib.pyplot as plt
from sklearn import datasets
from sklearn.preprocessing import StandardScaler
from matplotlib.colors import ListedColormap

def plot_decision_boundary(model, axis):#绘制分类区间的函数

    x0, x1 = np.meshgrid(#生产网格数据
        np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1, 1),
        np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1, 1),
    )
    X_new = np.c_[x0.ravel(), x1.ravel()]
    #np.c_是按行连接两个矩阵，就是把两矩阵左右相加，要求行数相等。
    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)   
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    
    plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)#绘制等高线图

iris = datasets.load_iris()#引入iris数据集

X = iris.data
y = iris.target
# 只取前两个特征
X = X[y<2,:2]
y = y[y<2]

standardScaler = StandardScaler()
standardScaler.fit(X)
X_standard = standardScaler.transform(X)#对数据进行归一化

clf = svm.SVC(kernel='linear',C=0.00000001)#使用线性分类
clf.fit(X_standard,y)
    
plot_decision_boundary(clf, axis=[-3, 3, -3,3])
plt.scatter(X_standard[y==0,0], X_standard[y==0,1], color='red')
plt.scatter(X_standard[y==1,0], X_standard[y==1,1], color='blue')
plt.show()

当C=0.4时的分类情况

当C=0.00000001时的分类情况

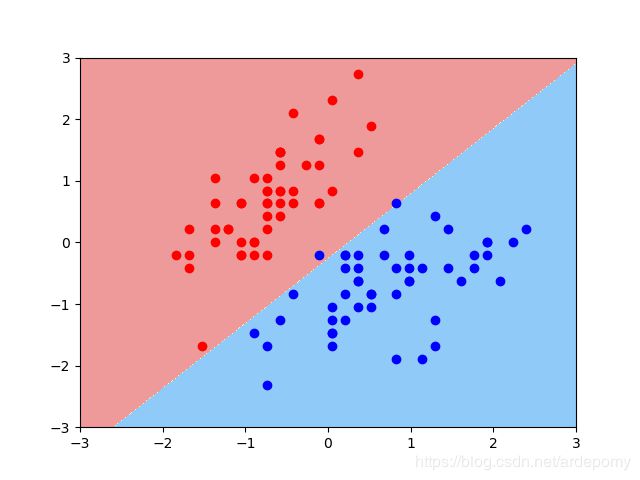
实现过程记录

发现对sklearn还不熟悉，只好在学习吴恩达课程的同时摸摸sklearn的各种功能
sklearn中实现SVM的函数的参数说明：

sklearn.svm.SVC(C=1.0, kernel='rbf', degree=3, gamma='auto', coef0=0.0, shrinking=True, probability=False,
tol=0.001, cache_size=200, class_weight=None, verbose=False, max_iter=-1, decision_function_shape=None,random_state=None)

参数：

C：C-SVC的惩罚参数C?默认值是1.0
''' C越大，相当于惩罚松弛变量，希望松弛变量接近0，即对误分类的惩罚增大，趋向于对训练集全分对的情况，这样对训练集测试时准确率很高，但泛化能力弱。C值小，对误分类的惩罚减小，允许容错，将他们当成噪声点，泛化能力较强。 '''
kernel ：核函数，默认是rbf，可以是‘linear’, ‘poly’, ‘rbf’, ‘sigmoid’, ‘precomputed’ 
''' 　　0 – 线性：u'v 　　 1 – 多项式：(gamma*u'*v + coef0)^degree 　　2 – RBF函数：exp(-gamma|u-v|^2) 　　3 –sigmoid：tanh(gamma*u'*v + coef0) '''
degree ：多项式poly函数的维度，默认是3，选择其他核函数时会被忽略。

gamma ： ‘rbf’,‘poly’ 和‘sigmoid’的核函数参数。默认是’auto’，则会选择1/n_features

coef0 ：核函数的常数项。对于‘poly’和 ‘sigmoid’有用。

probability ：是否采用概率估计？.默认为False

shrinking ：是否采用shrinking heuristic方法，默认为true

tol ：停止训练的误差值大小，默认为1e-3

cache_size ：核函数cache缓存大小，默认为200

class_weight ：类别的权重，字典形式传递。设置第几类的参数C为weight*C(C-SVC中的C)

verbose ：允许冗余输出？

max_iter ：最大迭代次数。-1为无限制。

decision_function_shape ：‘ovo’, ‘ovr’ or None, default=None3

random_state ：数据洗牌时的种子值，int值

主要调节的参数有：C、kernel、degree、gamma、coef0。
sklearn是个极其方便的库，本来要写一大段才能实现的算法，现在只需要fit一下就好了。

公式部分

SVM原本的损失函数公式：

$$\frac{1}{m}[\sum _{i=1}^m(y^{(i)}cos{t}_1({\theta }^T{x}^{(i)})+(1-y^{(i)})cos{t}_0({\theta }^T{x}^{(i)}))+\frac{\lambda }{2}\sum _{j=0}^m{\theta }_j^2]$$
式中cost1()和cost0()分别等于
$$-log{h}_{\theta }(x^{(i)}).-log(1-h_{\theta }(x^{(i)})).$$
将式中第一个求和部分看做A，第二个求和部分看做B，则最小化目标可以变为A+λB,也可写作CA+B,其中C等于1/λ
最终的损失函数公式：
$$C[\sum _{i=1}^m(y^{(i)}cos{t}_1({\theta }^T{x}^{(i)})+(1-y^{(i)})cos{t}_0({\theta }^T{x}^{(i)}))]+\frac{1}{2}\sum _{i=0}^m{\theta }_i^2$$

引用

sklearn系列之 sklearn.svm.SVC详解
svm代码实现

学习视频

SVM

其他笔记

• 机器学习入门
  - 目录