免费赠书 | 房价的一元回归分析
文末赠书活动,欢迎参加
在统计学中,回归分析(regression analysis)指的是确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。该方法常使用数据统计的基本原理,对大量统计数据进行数学处理,并确定因变量与某些自变量的相关关系,建立一个相关性较好的回归方程(函数表达式),并加以外推,用于预测今后的因变量的变化的分析方法。
大家对最近的楼市价格都深有体会,这一年中楼市可谓是风起云诵,跌宕起伏。为了控制房价,国家相继出台各种调控政策,楼市调控政策持续时间之长,各种政策齐头并进,这在国内房地产历史上也是少有的。能否根据各种条件预测房价呢,在这个实例中,我们考虑一个简单的一元回归分析问题,来预测房价。
假设数据集如下所示:
通过上面的数据分析,可以看出,房价和房子大小之间是有相关关系的,下面是用这组数据,来预测任意大小的房子的房价。基本步骤类似前面介绍的身高和体重之间的模型构建。
前面身高和体重的一元回归分析中已经详细介绍了实现方法,主要是使用scikitlearn中的LinearRegression模型来建立回归模型,并且使用LinearRegression模型中的两个基本方法, fit() 和 predict()方法。其中fit() 用来分析模型参数,predict() 是通过 fit() 算出的模型参数构成的模型,对自变量进行预测来获得其值。
为了使程序更加易于使用和管理,我们这次把数据存放到一个文件中,并且定义一个预测函数,输入训练集参数和要预测的值,最后得到预测结果。
事先把上面数据存放在一个house_price.csv文件中。如下所示:
首先编写一个函数,输入这个文件,然后把房间大小和价格的数据转换成scikitlearn中的LinearRegression模型可以识别的数据,程序如下:
def get_data(file_name):
data = pd.read_csv(file_name)
X_parameter = []
Y_parameter = []
for single_meter_feet,single_price_value in zip(data['square_meter'],data['price']):
X_parameter.append([float(single_square_meter)])
Y_parameter.append(float(single_price_value))
return X_parameter,Y_parameter
这个函数中使用Pandas的read_csv方法将.csv数据读入数据帧,然后把Pandas数据帧转换为X_parameter和Y_parameter数据。
当数据从csv文件中读取后,定义一个函数,在函数中进来模型,并使用训练数据进行训练,然后使用训练好的模型对需要预测的数据进行预测,并返回结果,代码如下:
def linear_model_main(X_parameter,Y_parameter,predict_square_meter):
# 1. 构造回归对象
regr = LinearRegression()
regr.fit(X_parameter,Y_parameter)
# 2. 获取预测值
predict_outcome = regr.predict(predict_square_meter)
# 3. 构造返回字典
predictions = {}
# 3.1 截距值
predictions['intercept'] = regr.intercept_
# 3.2 回归系数(斜率值)
predictions['coefficient'] = regr.coef_
# 3.3 预测值
predictions['predict_value'] = predict_outcome
return predictions
其中使用了LinearRegression模型中的两个基本方法: fit() 和 predict()方法。
最后我们建立一个简单图像处理函数,显示运行结果,代码如下所示:
def show_linear_line(X_parameter,Y_parameter):
# 1. 构造回归对象
regr = LinearRegression()
regr.fit(X_parameter,Y_parameter)
# 2. 绘出已知数据散点图
plt.scatter(X_parameter,Y_parameter,color = 'blue')
# 3. 绘出预测直线
plt.plot(X_parameter,regr.predict(X_parameter),color = 'red',linewidth = 4)
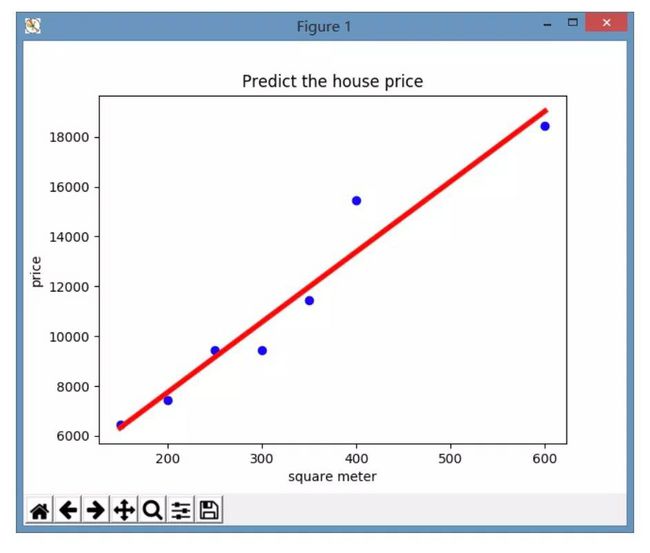
plt.title('Predict the house price')
plt.xlabel('square meter')
plt.ylabel('price')
plt.show()
最终显示结果如下图所示:
此外,计算的截距和系数,以及预测值如下所示:
intercept:2085.6382978723395
coefficient:[ 28.24468085]
predict_value:[ 21856.91489362]
可以发现,数据基本符合一元回归模型。
文章节选自北京大学出版社出版的《Python 3 数据分析与机器学习实战》,这本书现在在京东参加满100减50的活动,点击阅读原文,即可了解更多。书香节优惠码 :G469NF,4月16号至25号可用,在每满100减50的基础上使用该优惠码满200元再减30元。
在文章底部留言区说说你用Python做过的印象最深刻的项目。本文留言区点赞数排名前10名的朋友,可以免费获得《Python3数据分析与机器学习实战》图书一本, 奖品图书由北京大学出版社提供。
活动截止日期:4月25日(周四)晚上22:00。