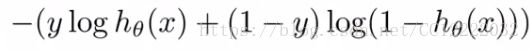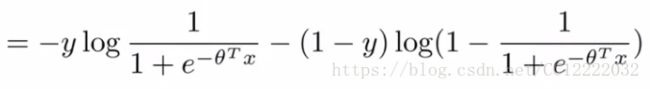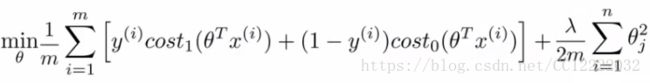吴恩达机器学习总结:第九课 支持向量机(大纲摘要及课后作业)
为了更好的学习,充分复习自己学习的知识,总结课内重要知识点,每次完成作业后都会更博。
英文非官方笔记
总结
1.支持向量机——优化对象
(1)另一种替代的对于逻辑回归的视角
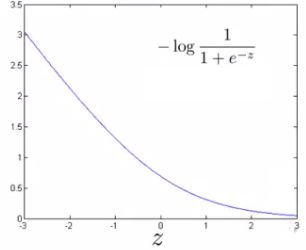
a.逻辑回归假设,和sigmoid函数图,以及代价函数
b.将(hθ(x))代入代价函数,得到另外一种形式代价函数
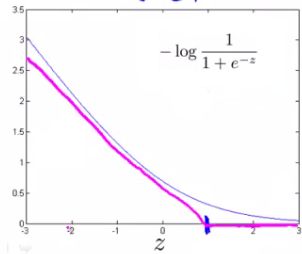
y=1和y=0时,代价函数曲线
(2)从逻辑回归代价函数中得到SVM的代价函数
a.SVM曲线
b.定义 cost1(z)和 cost0(z)
(3)完全形式代价函数
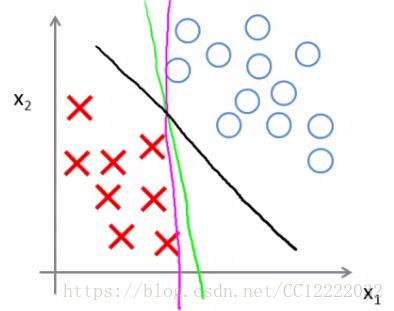
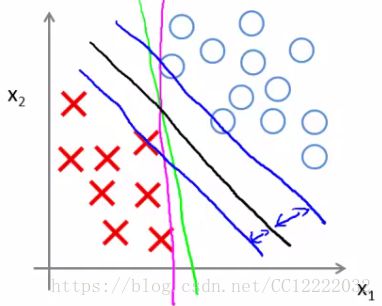
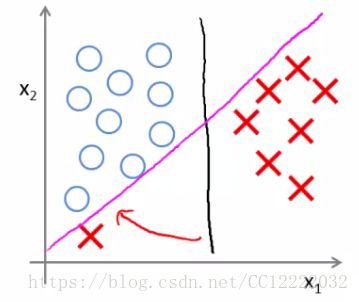
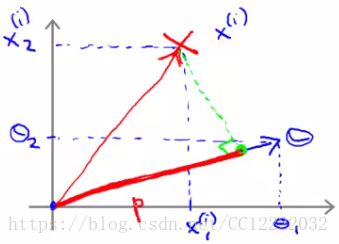
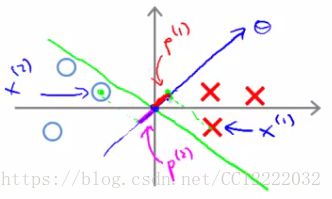
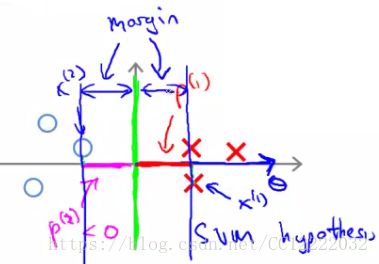
2.大边缘直观理解
3.大边缘分类器数学方法
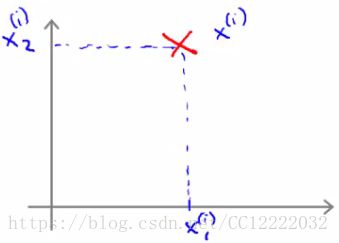
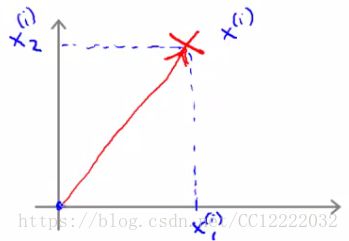
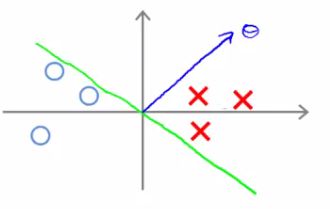
4.内核——针对非线性分类器的自适应SVM
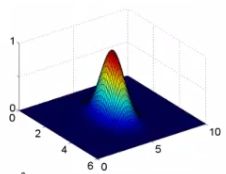
(1)f1= exp(- (|| x - l1 ||2 ) / 2σ2) (高斯内核)
(2)深入理解内核
a.σ2 = 0.5
b.σ2 = 0.5
c.σ2 = 0.5
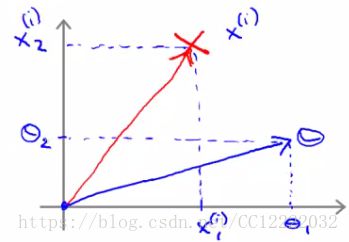
5.内核II
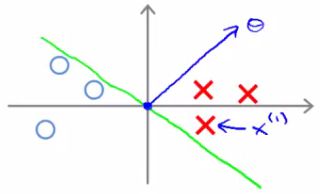
(1)选择标记点
a.f0 = 1
b.f1i, = k(xi, l1),f2i, = k(xi, l2),...,fmi, = k(xi, lm)
(2)带内核SVM假设预测
a.代价函数
b.SVM参数C(很大C造成假设低偏差高方差,过拟合;很小C造成假设高偏差低方差,欠拟合)
c.SVM参数σ(很大σ造成f特征变化平滑,更高偏差哥更低方差;很小σ造成f特征变化很突兀,低偏差,高方差)
6.SVM实施
(1)选择参数C和内核
(2)高斯内核,线性内核,多项式内核,字符串内核,卡方内核,直方图交叉内核
作业
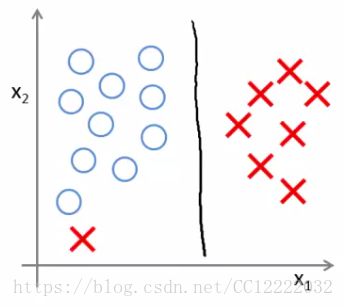
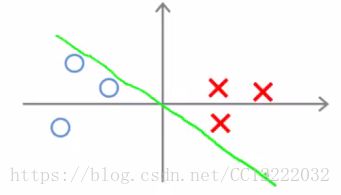
1.(1)载入及可视化
clear ; close all; clc
load('ex6data1.mat');
plotData(X, y);
%plotData 函数
pos = find(y == 1); neg = find(y == 0);
plot(X(pos, 1), X(pos, 2), 'k+','LineWidth', 1, 'MarkerSize', 7)
hold on;
plot(X(neg, 1), X(neg, 2), 'ko', 'MarkerFaceColor', 'y', 'MarkerSize', 7)
hold off;
end
(2)训练线性SVM
load('ex6data1.mat');
C = 1;
model = svmTrain(X, y, C, @linearKernel, 1e-3, 20);
visualizeBoundaryLinear(X, y, model);
%svmTrain 函数
if ~exist('tol', 'var') || isempty(tol)
tol = 1e-3;
end
if ~exist('max_passes', 'var') || isempty(max_passes)
max_passes = 5;
end
m = size(X, 1);
n = size(X, 2);
Y(Y==0) = -1;
alphas = zeros(m, 1);
b = 0;
E = zeros(m, 1);
passes = 0;
eta = 0;
L = 0;
H = 0;
if strcmp(func2str(kernelFunction), 'linearKernel')
K = X*X';
elseif strfind(func2str(kernelFunction), 'gaussianKernel')
X2 = sum(X.^2, 2);
K = bsxfun(@plus, X2, bsxfun(@plus, X2', - 2 * (X * X')));
K = kernelFunction(1, 0) .^ K;
else
K = zeros(m);
for i = 1:m
for j = i:m
K(i,j) = kernelFunction(X(i,:)', X(j,:)');
K(j,i) = K(i,j); %the matrix is symmetric
end
end
end
dots = 12;
while passes < max_passes,
num_changed_alphas = 0;
for i = 1:m,
E(i) = b + sum (alphas.*Y.*K(:,i)) - Y(i);
if ((Y(i)*E(i) < -tol && alphas(i) < C) || (Y(i)*E(i) > tol && alphas(i) > 0)),
j = ceil(m * rand());
while j == i, % Make sure i \neq j
j = ceil(m * rand());
end
E(j) = b + sum (alphas.*Y.*K(:,j)) - Y(j);
alpha_i_old = alphas(i);
alpha_j_old = alphas(j);
if (Y(i) == Y(j)),
L = max(0, alphas(j) + alphas(i) - C);
H = min(C, alphas(j) + alphas(i));
else
L = max(0, alphas(j) - alphas(i));
H = min(C, C + alphas(j) - alphas(i));
end
if (L == H),
continue;
end
eta = 2 * K(i,j) - K(i,i) - K(j,j);
if (eta >= 0),
% continue to next i.
continue;
end
alphas(j) = alphas(j) - (Y(j) * (E(i) - E(j))) / eta;
alphas(j) = min (H, alphas(j));
alphas(j) = max (L, alphas(j));
if (abs(alphas(j) - alpha_j_old) < tol),
% continue to next i.
% replace anyway
alphas(j) = alpha_j_old;
continue;
end
alphas(i) = alphas(i) + Y(i)*Y(j)*(alpha_j_old - alphas(j));
b1 = b - E(i) ...
- Y(i) * (alphas(i) - alpha_i_old) * K(i,j)' ...
- Y(j) * (alphas(j) - alpha_j_old) * K(i,j)';
b2 = b - E(j) ...
- Y(i) * (alphas(i) - alpha_i_old) * K(i,j)' ...
- Y(j) * (alphas(j) - alpha_j_old) * K(j,j)';
if (0 < alphas(i) && alphas(i) < C),
b = b1;
elseif (0 < alphas(j) && alphas(j) < C),
b = b2;
else
b = (b1+b2)/2;
end
num_changed_alphas = num_changed_alphas + 1;
end
end
if (num_changed_alphas == 0),
passes = passes + 1;
else
passes = 0;
end
fprintf('.');
dots = dots + 1;
if dots > 78
dots = 0;
fprintf('\n');
end
if exist('OCTAVE_VERSION')
fflush(stdout);
end
end
fprintf(' Done! \n\n');
idx = alphas > 0;
model.X= X(idx,:);
model.y= Y(idx);
model.kernelFunction = kernelFunction;
model.b= b;
model.alphas= alphas(idx);
model.w = ((alphas.*Y)'*X)';
end
%visualizeBoundaryLinear函数
w = model.w;
b = model.b;
xp = linspace(min(X(:,1)), max(X(:,1)), 100);
yp = - (w(1)*xp + b)/w(2);
plotData(X, y);
hold on;
plot(xp, yp, '-b');
hold off
end
(3)实施高斯内核
x1 = [1 2 1]; x2 = [0 4 -1]; sigma = 2;
sim = gaussianKernel(x1, x2, sigma);
%高斯内核函数
x1 = x1(:); x2 = x2(:);
sim = 0;
sim = exp(-1/(2*sigma*sigma)*(sum((x1-x2).^2)));
(4)可视化数据集2
load('ex6data2.mat');
plotData(X, y);
(5)训练RBF内核的SVM
load('ex6data2.mat');
C = 1; sigma = 0.1;
model= svmTrain(X, y, C, @(x1, x2) gaussianKernel(x1, x2, sigma));
visualizeBoundary(X, y, model);
%visualizeBoundary函数
plotData(X, y)
x1plot = linspace(min(X(:,1)), max(X(:,1)), 100)';
x2plot = linspace(min(X(:,2)), max(X(:,2)), 100)';
[X1, X2] = meshgrid(x1plot, x2plot);
vals = zeros(size(X1));
for i = 1:size(X1, 2)
this_X = [X1(:, i), X2(:, i)];
vals(:, i) = svmPredict(model, this_X);
end
hold on
contour(X1, X2, vals, [0.5 0.5], 'b');
hold off;
end
(6)可视化数据集3并且训练SVM
load('ex6data3.mat');
plotData(X, y);
[C, sigma] = dataset3Params(X, y, Xval, yval);
model= svmTrain(X, y, C, @(x1, x2) gaussianKernel(x1, x2, sigma));
visualizeBoundary(X, y, model);
2(1)邮件生成
file_contents = readFile('emailSample1.txt');
word_indices = processEmail(file_contents);(2)特征提取
file_contents = readFile('emailSample1.txt');
word_indices = processEmail(file_contents);
features = emailFeatures(word_indices);(3)为垃圾邮件分类训练线性内核
load('spamTrain.mat');
C = 0.1;
model = svmTrain(X, y, C, @linearKernel);
p = svmPredict(model, X);(4)测试邮件分类器
load('spamTest.mat');
p = svmPredict(model, Xtest);(5)垃圾邮件预测
[weight, idx] = sort(model.w, 'descend');
vocabList = getVocabList();
fprintf('\nTop predictors of spam: \n');
for i = 1:15
fprintf(' %-15s (%f) \n', vocabList{idx(i)}, weight(i));
end(6)尝试自己的邮件
filename = 'spamSample1.txt';
file_contents = readFile(filename);
word_indices = processEmail(file_contents);
x = emailFeatures(word_indices);
p = svmPredict(model, x);