Python3.6实现常用数据结构和算法(链表和二叉树经典问题，八大排序和三大查找)

前言

Python大法好，除了工作用的OC外，其他时间Python还是很好用的，比如刷题，写脚本，美滋滋。。。

数据结构只是静态的描述了数据元素之间的关系。

高效的程序需要在数据结构的基础上设计和选择算法。

程序 = 数据结构 + 算法

总结：算法是为了解决实际问题而设计的，数据结构是算法需要处理的问题载体

抽象数据类型(ADT)的含义是指一个数学模型以及定义在此数学模型上的一组操作。即把数据类型和数据类型上的运算捆在一起，进行封装。引入抽象数据类型的目的是把数据类型的表示和数据类型上运算的实现与这些数据类型和运算在程序中的引用隔开，使它们相互独立。

最常用的数据运算有五种：

• 插入
• 删除
• 修改
• 查找
• 排序

 

顺序表

在程序中，经常需要将一组（通常是同为某个类型的）数据元素作为整体管理和使用，需要创建这种元素组，用变量记录它们，传进传出函数等。一组数据中包含的元素个数可能发生变化（可以增加或删除元素）。

对于这种需求，最简单的解决方案便是将这样一组元素看成一个序列，用元素在序列里的位置和顺序，表示实际应用中的某种有意义的信息，或者表示数据之间的某种关系。

这样的一组序列元素的组织形式，我们可以将其抽象为线性表。一个线性表是某类元素的一个集合，还记录着元素之间的一种顺序关系。线性表是最基本的数据结构之一，在实际程序中应用非常广泛，它还经常被用作更复杂的数据结构的实现基础。

根据线性表的实际存储方式，分为两种实现模型：

• 顺序表，将元素顺序地存放在一块连续的存储区里，元素间的顺序关系由它们的存储顺序自然表示。
• 链表，将元素存放在通过链接构造起来的一系列存储块中。

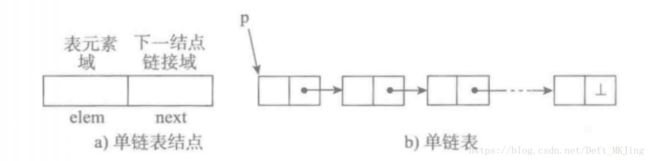
图a表示的是顺序表的基本形式，数据元素本身连续存储，每个元素所占的存储单元大小固定相同，元素的下标是其逻辑地址，而元素存储的物理地址（实际内存地址）可以通过存储区的起始地址Loc (e0)加上逻辑地址（第i个元素）与存储单元大小（c）的乘积计算而得，即：

Loc(ei) = Loc(e0) + c*i

故，访问指定元素时无需从头遍历，通过计算便可获得对应地址，其时间复杂度为O(1)。

tip：数据存储在内存中根据类型分配字节，例如32位机器中int是4个字节，char是一个字节，那么一个字节就是八位 0000 0000，当我们把一个int类型存储进去的时候，会占有4个字节也就就是32位，用0填充，计算机去查找的时候，根据首地址偏移4个字节，组合起来就是对应的数组，如果char类型，偏移一个字节，拿出来匹配char类型

如果元素的大小不统一，则须采用图b的元素外置的形式，将实际数据元素另行存储，而顺序表中各单元位置保存对应元素的地址信息（即链接）。由于每个链接所需的存储量相同，通过上述公式，可以计算出元素链接的存储位置，而后顺着链接找到实际存储的数据元素。注意，图b中的c不再是数据元素的大小，而是存储一个链接地址所需的存储量，这个量通常很小。

图b这样的顺序表也被称为对实际数据的索引，这是最简单的索引结构。

可以看到图a是存储的实际同类型的数据，而图b存储的是不同类型的数据（但是存储的是数据的指针 64位 8字节固定）

顺序表实现和结构

一个顺序表的完整信息包括两部分，一部分是表中的元素集合，另一部分是为实现正确操作而需记录的信息，即有关表的整体情况的信息，这部分信息主要包括元素存储区的容量和当前表中已有的元素个数两项。

图a为一体式结构，存储表信息的单元与元素存储区以连续的方式安排在一块存储区里，两部分数据的整体形成一个完整的顺序表对象。

一体式结构整体性强，易于管理。但是由于数据元素存储区域是表对象的一部分，顺序表创建后，元素存储区就固定了。

图b为分离式结构，表对象里只保存与整个表有关的信息（即容量和元素个数），实际数据元素存放在另一个独立的元素存储区里，通过链接与基本表对象关联。

一体式结构由于顺序表信息区与数据区连续存储在一起，所以若想更换数据区，则只能整体搬迁，即整个顺序表对象（指存储顺序表的结构信息的区域）改变了。

分离式结构若想更换数据区，只需将表信息区中的数据区链接地址更新即可，而该顺序表对象不变。

采用分离式结构的顺序表，若将数据区更换为存储空间更大的区域，则可以在不改变表对象的前提下对其数据存储区进行了扩充，所有使用这个表的地方都不必修改。只要程序的运行环境（计算机系统）还有空闲存储，这种表结构就不会因为满了而导致操作无法进行。人们把采用这种技术实现的顺序表称为动态顺序表，因为其容量可以在使用中动态变化。

Python中的顺序表

Python中的list和tuple两种类型采用了顺序表的实现技术，具有前面讨论的顺序表的所有性质。

tuple是不可变类型，即不变的顺序表，因此不支持改变其内部状态的任何操作，而其他方面，则与list的性质类似。

list的基本实现技术

Python标准类型list就是一种元素个数可变的线性表，可以加入和删除元素，并在各种操作中维持已有元素的顺序（即保序），而且还具有以下行为特征：

• 基于下标（位置）的高效元素访问和更新，时间复杂度应该是O(1)；

  为满足该特征，应该采用顺序表技术，表中元素保存在一块连续的存储区中。

• 允许任意加入元素，而且在不断加入元素的过程中，表对象的标识（函数id得到的值）不变。

  为满足该特征，就必须能更换元素存储区，并且为保证更换存储区时list对象的标识id不变，只能采用分离式实现技术。

在Python的官方实现中，list就是一种采用分离式技术实现的动态顺序表。这就是为什么用list.append(x) （或 list.insert(len(list), x)，即尾部插入）比在指定位置插入元素效率高的原因。

在Python的官方实现中，list实现采用了如下的策略：在建立空表（或者很小的表）时，系统分配一块能容纳8个元素的存储区；在执行插入操作（insert或append）时，如果元素存储区满就换一块4倍大的存储区。但如果此时的表已经很大（目前的阀值为50000），则改变策略，采用加一倍的方法。引入这种改变策略的方式，是为了避免出现过多空闲的存储位置。

 

OC中NSMutableArray的实现技术

之前也有文章探讨过NSMutableArray的底层，分离式那是肯定的，动态扩容，不光如此，NSMutableArray还实现了环形缓冲区数据结构，让插入保序的情况下尽可能少的移动内存地址进行插入或者删除

NSMutableArray和NSDictionary底层实现

 

链表

为什么需要链表

可以根据上面的介绍顺序表可以看出

1.顺序表的构建需要预先知道数据大小来申请连续的存储空间，

2.而在进行扩充时又需要进行数据的搬迁，所以使用起来并不是很灵活。

链表结构可以充分利用计算机内存空间，实现灵活的内存动态管理。

链表（Linked list）是一种常见的基础数据结构，是一种线性表，但是不像顺序表一样连续存储数据，而是在每一个节点（数据存储单元）里存放下一个节点的位置信息（即地址）。

单链表

单向链表也叫单链表，是链表中最简单的一种形式，它的每个节点包含两个域，一个信息域（元素域）和一个链接域。这个链接指向链表中的下一个节点，而最后一个节点的链接域则指向一个空值。

代码实现

class Node(object):
    """节点创建"""

    def __init__(self, item):
        self.ele = item
        self.next = None


class SingleNodeList(object):
    """链表创建 可以带参，也可以不带"""

    def __init__(self, node=None):
        # 不带参数就是None
        self.__head = node

    def is_empty(self):
        """链表是否为空"""
        return self.__head is None

    def length(self):
        """链表长度"""
        cur = self.__head
        count = 0
        # 遍历
        while cur is not None:
            cur = cur.next
            count += 1
        return count

    def travel(self):
        """遍历整个链表"""
        cur = self.__head
        while cur is not None:
            print(cur.ele, end=" ")
            cur = cur.next
        print("")

    def add(self, item):
        """链表头部添加元素"""
        node = Node(item)
        node.next = self.__head
        self.__head = node

    def append(self, item):
        """链表尾部添加元素"""
        if self.is_empty():
            self.__head = Node(item)
            return
        cur = self.__head
        while cur.next is not None:
            cur = cur.next
        cur.next = Node(item)

    def insert(self, pos, item):
        """
        指定位置添加元素
        :param pos: 0开始
        :param item: 插入元素
        :return: None
        """
        # 头插
        if pos <= 0:
            self.add(item)
        # 尾插
        elif pos >= self.length():
            self.append(item)
        # 中间插入
        else:
            pre = self.__head
            index = 0
            while index < pos - 1:
                pre = pre.next
                index += 1
            # 插入节点先链接，然后再改变游标原有next
            node = Node(item)
            node.next = pre.next
            pre.next = node

    def remove(self, item):
        """删除节点"""
        pre = None
        cur = self.__head
        
        while cur is not None:
            # 匹配到
            if cur.ele == item:
                # 第一个元素单独处理
                if cur == self.__head:
                    self.__head = cur.next
                else:
                    # 其他元素用pre指针和cur指针操作
                    pre.next = cur.next
                break
            else:
                # 往后移动
                pre = cur
                cur = cur.next

    def search(self, item):
        """查找节点是否存在"""
        cur = self.__head
        while cur is not None:
            if cur.ele == item:
                return True
            else:
                cur = cur.next
        return False


if __name__ == "__main__":
    nodeList = SingleNodeList()

    nodeList.append(1)
    nodeList.add(100)
    nodeList.append(6)
    nodeList.add((0))
    nodeList.insert(7, 200)
    nodeList.insert(-1, 300)
    nodeList.insert(11, 400)

    print(nodeList.is_empty())
    print(nodeList.length())
    nodeList.travel()

    nodeList.remove(0)
    nodeList.travel()

链表失去了顺序表随机读取的优点，同时链表由于增加了结点的指针域，空间开销比较大，但对存储空间的使用要相对灵活。

链表与顺序表的各种操作复杂度如下所示：

操作	链表	顺序表
访问元素	O(n)	O(1)
在头部插入/删除	O(1)	O(n)
在尾部插入/删除	O(n)	O(1)
在中间插入/删除	O(n)	O(n)

注意虽然表面看起来复杂度都是 O(n)，但是链表和顺序表在插入和删除时进行的是完全不同的操作。链表的主要耗时操作是遍历查找，删除和插入操作本身的复杂度是O(1)。顺序表查找很快，主要耗时的操作是拷贝覆盖。因为除了目标元素在尾部的特殊情况，顺序表进行插入和删除时需要对操作点之后的所有元素进行前后移位操作，只能通过拷贝和覆盖的方法进行。

 

单向循环链表

单链表的一个变形是单向循环链表，链表中最后一个节点的next域不再为None，而是指向链表的头节点。

class Node(object):
    """节点创建"""

    def __init__(self, item):
        self.ele = item
        self.next = None


class SingleCycleNodeList(object):
    """循环单链表创建 可以带参，也可以不带"""

    def __init__(self, node=None):
        # 不带参数就是None
        self.__head = node
        # 参node初始化的时候需要循环指
        if node:
            node.next = self.__head

    def is_empty(self):
        """链表是否为空"""
        return self.__head is None

    def length(self):
        """链表长度"""
        if self.is_empty():
            return 0
        cur = self.__head
        count = 1
        # 遍历
        while cur.next != self.__head:
            cur = cur.next
            count += 1
        return count

    def travel(self):
        """遍历整个链表"""
        if self.is_empty()  :
            return
        cur = self.__head
        while cur.next != self.__head:
            print(cur.ele, end=" ")
            cur = cur.next
        print(cur.ele, end=" ")
        print("")

    def add(self, item):
        """链表头部添加元素"""
        node = Node(item)
        if self.is_empty():
            self.__head = node
            node.next = self.__head
        # 遍历拿到尾节点
        near = self.__head
        while near.next != self.__head:
            near = near.next

        node.next = self.__head
        self.__head = node
        near.next = self.__head

    def append(self, item):
        """链表尾部添加元素"""
        node = Node(item)
        if self.is_empty():
            self.__head = node
            node.next = self.__head
            return
        cur = self.__head
        while cur.next != self.__head:
            cur = cur.next
        cur.next = node
        node.next = self.__head

    def insert(self, pos, item):
        """
        指定位置添加元素
        :param pos: 0开始
        :param item: 插入元素
        :return: None
        """
        # 头插
        if pos <= 0:
            self.add(item)
        # 尾插
        elif pos >= self.length():
            self.append(item)
        # 中间插入
        else:
            pre = self.__head
            index = 0
            while index < pos - 1:
                pre = pre.next
                index += 1
            # 插入节点先链接，然后再改变游标原有next
            node = Node(item)
            node.next = pre.next
            pre.next = node

    def remove(self, item):
        """删除节点"""
        if self.is_empty():
            return
        pre = None
        cur = self.__head

        while cur.next != self.__head:
            # 匹配到
            if cur.ele == item:
                # 头删除 需要遍历获取尾节点来重新定位新头
                if cur == self.__head:
                    near = self.__head
                    while near.next != self.__head:
                        near = near.next

                    self.__head = cur.next
                    near.next = self.__head
                else:
                    # 其他元素用pre指针和cur指针操作 中间删除
                    pre.next = cur.next
                return
            else:
                # 往后移动
                pre = cur
                cur = cur.next
        # 最后一个元素删除
        if cur.ele == item:
            if cur == self.__head:
                self.__head = None
            else:
                pre.next = cur.next

    def search(self, item):
        """查找节点是否存在"""
        if self.is_empty():
            return False
        cur = self.__head
        while cur.next != self.__head:
            if cur.ele == item:
                return True
            else:
                cur = cur.next
        if cur.ele == item:
            return True
        return False


if __name__ == "__main__":
    nodeList = SingleCycleNodeList(Node(999))

    nodeList.append(1)
    nodeList.add(100)
    nodeList.append(6)
    nodeList.add((0))
    nodeList.insert(7, 200)
    nodeList.insert(-1, 300)
    nodeList.insert(11, 400)

    print(nodeList.is_empty())
    print(nodeList.length())
    nodeList.travel()

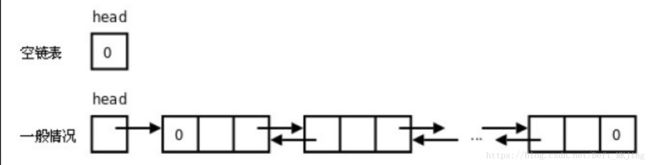
双向链表

一种更复杂的链表是“双向链表”或“双面链表”。每个节点有两个链接：一个指向前一个节点，当此节点为第一个节点时，指向空值；而另一个指向下一个节点，当此节点为最后一个节点时，指向空值。

class Node(object):
    """节点创建"""

    def __init__(self, item):
        self.ele = item
        self.next = None
        self.prev = None


class SingleNodeList(object):
    """双链表创建 可以带参，也可以不带"""

    def __init__(self, node=None):
        # 不带参数就是None
        self.__head = node

    def is_empty(self):
        """链表是否为空"""
        return self.__head is None

    def length(self):
        """链表长度"""
        cur = self.__head
        count = 0
        # 遍历
        while cur is not None:
            cur = cur.next
            count += 1
        return count

    def travel(self):
        """遍历整个链表"""
        cur = self.__head
        while cur is not None:
            print(cur.ele, end=" ")
            cur = cur.next
        print("")

    def add(self, item):
        """链表头部添加元素"""
        node = Node(item)
        if self.is_empty():
            self.__head = node
            return
        node.next = self.__head
        self.__head.prev = node
        self.__head = node

    def append(self, item):
        """链表尾部添加元素"""
        node = Node(item)
        if self.is_empty():
            self.__head = node
            return
        cur = self.__head
        while cur.next is not None:
            cur = cur.next
        cur.next = node
        node.prev = cur

    def insert(self, pos, item):
        """
        指定位置添加元素
        :param pos: 0开始
        :param item: 插入元素
        :return: None
        由于是双向链表，因此这里就不需要pre指针，只需要一个cur指针即可
        """
        # 头插
        if pos <= 0:
            self.add(item)
        # 尾插
        elif pos >= self.length():
            self.append(item)
        # 中间插入
        else:
            cur = self.__head
            index = 0
            while index < pos:
                cur = cur.next
                index += 1
            # 插入节点先链接，然后再改变游标原有next
            node = Node(item)
            node.next = cur
            node.prev = cur.prev
            cur.prev.next = node
            cur.prev = node

    def remove(self, item):
        """删除节点"""
        if self.is_empty():
            return
        cur = self.__head
        while cur is not None:
            # 匹配到
            if cur.ele == item:
                # 第一个元素单独处理
                if cur == self.__head:
                    self.__head = cur.next
                    self.__head.prev = None

                else:
                    cur.prev.next = cur.next
                    if cur.next:
                        # 删除尾部
                        cur.next.prev = cur.prev
                return
            else:
                cur = cur.next

    def search(self, item):
        """查找节点是否存在"""
        if self.is_empty():
            print("链表为空")
            return
        cur = self.__head
        while cur is not None:
            if cur.ele == item:
                print("prev-%s,cur-%s,next-%s"%(cur.prev.ele if cur.prev is not None else "空", cur.ele, cur.next.ele if cur.next is not None else "空"))
                return True
            else:
                cur = cur.next
        return False


if __name__ == "__main__":
    nodeList = SingleNodeList()

    nodeList.append(1)
    nodeList.add(100)
    nodeList.append(6)
    nodeList.add((0))
    nodeList.insert(7, 200)
    nodeList.insert(-1, 300)
    nodeList.insert(11, 400)

    print(nodeList.is_empty())
    print(nodeList.length())
    nodeList.travel()

    nodeList.remove(0)
    nodeList.travel()

    nodeList.remove(400)
    nodeList.travel()

    nodeList.remove(4000)
    nodeList.travel()

    nodeList.remove(300)
    nodeList.travel()

    nodeList.remove(3)
    nodeList.travel()

    print(nodeList.search(200))

 

 

以上是基本数据结构，负责数据如何存储，下方的高级抽象也就是合理使用基本数据类型，进行一定算法组合出来的高级抽象，提高API给用户使用 

 

栈和队列

栈

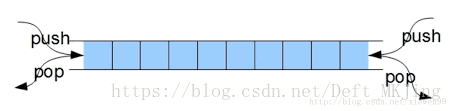
栈（stack），有些地方称为堆栈，是一种容器，可存入数据元素、访问元素、删除元素，它的特点在于只能允许在容器的一端（称为栈顶端指标，英语：top）进行加入数据（英语：push）和输出数据（英语：pop）的运算。没有了位置概念，保证任何时候可以访问、删除的元素都是此前最后存入的那个元素，确定了一种默认的访问顺序。

由于栈数据结构只允许在一端进行操作，因而按照后进先出（LIFO, Last In First Out）的原理运作。

可以用顺序表实现，也可以用链表实现，例如一个push的操作，如果用list实现，就是O(1),但是用链表实现，就是O(n)，因此内存具体用哪种操作，都是取决于是否可以最合理的时间复杂度

class Stack(object):
    """栈"""
    def __init__(self):
         self.items = []

    def is_empty(self):
        """判断是否为空"""
        return self.items == []

    def push(self, item):
        """加入元素"""
        self.items.append(item)

    def pop(self):
        """弹出元素"""
        return self.items.pop()

    def peek(self):
        """返回栈顶元素"""
        return self.items[len(self.items)-1]

    def size(self):
        """返回栈的大小"""
        return len(self.items)

if __name__ == "__main__":
    stack = Stack()
    stack.push("mi")
    stack.push("xiyue")
    stack.push("nice")
    print(stack.size())
    print(stack.peek())
    print(stack.pop())
    print(stack.pop())
    print(stack.pop())

队列

队列（queue）是只允许在一端进行插入操作，而在另一端进行删除操作的线性表。

队列是一种先进先出的（First In First Out）的线性表，简称FIFO。允许插入的一端为队尾，允许删除的一端为队头。队列不允许在中间部位进行操作！假设队列是q=（a1，a2，……，an），那么a1就是队头元素，而an是队尾元素。这样我们就可以删除时，总是从a1开始，而插入时，总是在队列最后。这也比较符合我们通常生活中的习惯，排在第一个的优先出列，最后来的当然排在队伍最后。

class Queue(object):
    """队列"""
    def __init__(self):
        self.items = []

    def is_empty(self):
        return self.items == []

    def enqueue(self, item):
        """进队列"""
        self.items.insert(0,item)

    def dequeue(self):
        """出队列"""
        return self.items.pop()

    def size(self):
        """返回大小"""
        return len(self.items)

if __name__ == "__main__":
    q = Queue()
    q.enqueue("mi")
    q.enqueue("xiyue")
    q.enqueue("Hi")
    print (q.size())
    print (q.dequeue())
    print (q.dequeue())
    print (q.dequeue())

双端队列 

双端队列（deque，全名double-ended queue），是一种具有队列和栈的性质的数据结构。

双端队列中的元素可以从两端弹出，其限定插入和删除操作在表的两端进行。双端队列可以在队列任意一端入队和出队。、

class Deque(object):
    """双端队列"""
    def __init__(self):
        self.items = []

    def is_empty(self):
        """判断队列是否为空"""
        return self.items == []

    def add_front(self, item):
        """在队头添加元素"""
        self.items.insert(0,item)

    def add_rear(self, item):
        """在队尾添加元素"""
        self.items.append(item)

    def remove_front(self):
        """从队头删除元素"""
        return self.items.pop(0)

    def remove_rear(self):
        """从队尾删除元素"""
        return self.items.pop()

    def size(self):
        """返回队列大小"""
        return len(self.items)


if __name__ == "__main__":
    deque = Deque()
    deque.add_front(1)
    deque.add_front(2)
    deque.add_rear(3)
    deque.add_rear(4)
    print (deque.size()) # 4
    # 2 1 4 3
    print (deque.remove_front()) # 2
    print (deque.remove_front()) # 1
    print (deque.remove_rear()) # 4
    print (deque.remove_rear()) # 3

 

基础排序算法

下面两个单独写出来了，一篇文章太多太长了

冒泡排序 选择排序 插入排序 快速排序 希尔排序 归并排序 

#  冒泡
class BubbtleSort():
    def sort(self, list):
        for i in range(len(list) - 1, 0, -1):
            for j in range(0, i):
                if list[j] > list[j + 1]:
                    list[j], list[j + 1] = list[j + 1], list[j]


# 选择
class selectSort():
    def sort(self, list):
        for i in range(0, len(list) - 1):
            min_index = i
            for j in range(i + 1, len(list)):
                if list[j] < list[min_index]:
                    min_index = j
            list[i], list[min_index] = list[min_index], list[i]


# 插入排序
class insertSort():
    def sort(self, list):
        # 1-6
        for i in range(1, len(list)):
            for j in range(i, 0, -1):
                if list[j] < list[j - 1]:
                    list[j], list[j - 1] = list[j - 1], list[j]

# 希尔排序
class xierSort():
    def sort(self, list):
        n = len(list)
        gap = n // 2

        while gap > 0:
            for i in range(gap, len(list)):
                for j in range(i, 0, -gap):
                    if list[j] < list[j - gap]:
                        list[j], list[j - gap] = list[j - gap], list[j]

            gap //= 2

# 快排
class quickSort():
    def sort(self, list, first, last):
        if first >= last:
            return
        mid = list[first]
        low = first
        high = last

        while low < high:
            while list[high] >= mid and low < high:
                high -= 1
            list[low] = list[high]
            while list[low] < mid and low < high:
                low += 1
            list[high] = list[low]
        list[low] = mid

        self.sort(list, first, low - 1)
        self.sort(list, low + 1, last)


# 归并排序
class merginSort():
    def sort(self, list):
        n = len(list)
        if n <= 1:
            return list
        mid = n // 2

        left_li = self.sort(list[:mid])
        right_li = self.sort(list[mid:])

        result = []
        left = 0
        right = 0

        while left < len(left_li) and right < len(right_li):
            # print(right_li)
            # print(left_li)
            if left_li[left] <= right_li[right]:
                result.append(left_li[left])
                left += 1
            else:
                result.append(right_li[right])
                right += 1
        result.extend(left_li[left:])
        result.extend(right_li[right:])

        return result


bubble = merginSort()
a = [54, 26, 83, 17, 77, 17, 31]
print(a)
b = bubble.sort(a)
print(a)
print(b)

花了几分钟写了下，你看看，python是不是刷题好帮手，这美感和代码量，爽 

经典排序算法详细介绍

 

二叉树和二分法

二叉树和二分法介绍

 

链表经典题目

题目列表： 以下是单链表基本结构，而且这些是核心思路，一些None，1个和2个的极端状况没考虑

class Node(object):
    """节点创建"""
    def __init__(self, item):
        self.ele = item
        self.next = None


def append(head,ele):
    cur = head
    if cur is None:
        cur = Node(ele)
        return
    while cur.next is not None:
        cur = cur.next
    cur.next = Node(ele)



# 打印
def travel(head):
    cur = head
    while cur is not None:
        print(cur.ele, end=" ")
        cur = cur.next

1. 求单链表中结点的个数

# 节点个数
def node_list_count(head):
    count = 0
    cur = head
    while cur is not None:
        cur = cur.next
        count += 1
    return count

2. 将单链表反转

# 翻转单链表
def reverse_list_node(head):

    pre = None
    while head is not None:
        cur = head
        head = cur.next
        cur.next = pre
        pre = cur
    return cur

3. 查找单链表中的倒数第K个结点（k > 0）

最普遍的方法是，先统计单链表中结点的个数，然后再找到第（n-k）个结点。注意链表为空，k为0，k为1，k大于链表中节点个数时的情况。时间复杂度为O（n）。代码略。 这里主要讲一下另一个思路，这种思路在其他题目中也会有应用。 主要思路就是使用两个指针，先让前面的指针走到正向第k个结点，这样前后两个指针的距离差是k-1，之后前后两个指针一起向前走，前面的指针走到最后一个结点时，后面指针所指结点就是倒数第k个结点。 

# 查找单链表中的倒数第K个结点（k > 0）
def last_index_node(head, k):

    # 这里有个越界判断
    print('倒数第%s个'%k)

    pre = head
    cur = head
    while k > 1 and pre is not None:
       pre = pre.next
       k -= 1

    while pre.next is not None:
        pre = pre.next
        cur = cur.next
    return cur.ele

4. 查找单链表的中间结点

此题可应用于上一题类似的思想。也是设置两个指针，只不过这里是，两个指针同时向前走，前面的指针每次走两步，后面的指针每次走一步，前面的指针走到最后一个结点时，后面的指针所指结点就是中间结点，即第（n/2+1）个结点。注意链表为空，链表结点个数为1和2的情况。时间复杂度O（n）。参考代码如下： 

# 查找单链表的中间结点
def search_mid_node(head):

    # 需要自己再添加1 2 和空的情况

    # 核心代码
    pre = head
    cur = head
    while pre.next is not None:
        pre = pre.next
        cur = cur.next
        # 这里考虑偶数或者奇数
        if pre.next is not None:
            pre = pre.next
    return cur.ele

5. 从尾到头打印单链表 （栈结构）

# 从尾到头打印单链表
def reverse_travel(head):
    cur = head
    list = []
    while cur is not None:
        list.append(cur)
        cur = cur.next

    while list:
        node = list.pop()
        print(node.ele, end=" ")

6. 已知两个单链表pHead1 和pHead2 各自有序，把它们合并成一个链表依然有序

这个类似归并排序。尤其注意两个链表都为空，和其中一个为空时的情况。只需要O（1）的空间。时间复杂度为O（max(len1, len2)）。参考代码如下： 

# 合并两个顺序链表
def mergin_node_list(headerNode1, headerNode2):
    if headerNode1 is None:
        return headerNode2
    if headerNode2 is None:
        return headerNode1
    temp = None
    if headerNode1.ele < headerNode2.ele:
        temp = headerNode1
        temp.next = mergin_node_list(headerNode1.next,headerNode2)
    else:
        temp = headerNode2
        temp.next = mergin_node_list(headerNode1, headerNode2.next)
    return temp

7. 判断一个单链表中是否有环

这里也是用到两个指针。如果一个链表中有环，也就是说用一个指针去遍历，是永远走不到头的。因此，我们可以用两个指针去遍历，一个指针一次走两步，一个指针一次走一步，如果有环，两个指针肯定会在环中相遇。时间复杂度为O（n）。参考代码如下 

# 判断链表是否有环
def hasCircle(head):

    cur = head
    pre = head

    while pre is not None and pre.next is not None:
        pre = pre.next.next
        cur = cur.next
        if pre == cur:
            return True
    return False

 

8. 判断两个单链表是否相交

如果两个链表相交于某一节点，那么在这个相交节点之后的所有节点都是两个链表所共有的。也就是说，如果两个链表相交，那么最后一个节点肯定是共有的。先遍历第一个链表，记住最后一个节点，然后遍历第二个链表，到最后一个节点时和第一个链表的最后一个节点做比较，如果相同，则相交，否则不相交。时间复杂度为O(len1+len2)，因为只需要一个额外指针保存最后一个节点地址，空间复杂度为O(1)。参考代码如下：

# 判断两个单链表是否相交
def isIntersected(head1,head2):

    p1 = head1
    p2 = head2

    while head1.next is not None:
        p1 = p1.next

    while head2.next is not None:
        p2 = p2.next

    return p1 == p2

9. 求两个单链表相交的第一个节点

对第一个链表遍历，计算长度len1，同时保存最后一个节点的地址。 对第二个链表遍历，计算长度len2，同时检查最后一个节点是否和第一个链表的最后一个节点相同，若不相同，不相交，结束。 两个链表均从头节点开始，假设len1大于len2，那么将第一个链表先遍历len1-len2个节点，此时两个链表当前节点到第一个相交节点的距离就相等了，然后一起向后遍历，知道两个节点的地址相同。 时间复杂度，O(len1+len2)。参考代码如下：

# 判断两个相交的链表的第一个节点
def getFirstCommondNode(head1,head2):

    p1 = head1
    len1 = 1
    p2 = head2
    len2 = 1

    while head1.next is not None:
        p1 = p1.next
        len1 += 1

    while head2.next is not None:
        p2 = p2.next
        len2 += 1

    if p1 != p2:
        return None

    node1 = head1
    node2 = head2
    if len1 > len2:
        k = len1 - len2

        while k > 0:
            node1 = node1.next
            k -= 1
    else:
        k = len2 - len1
        while k > 0:
            node2 = node2.next
            k -= 1

    while node1 != node2:
        node1 = node1.next
        node2 = node2.next
    return node1

 

10. 已知一个单链表中存在环，求进入环中的第一个节点

首先判断是否存在环，若不存在结束。在环中的一个节点处断开（当然函数结束时不能破坏原链表），这样就形成了两个相交的单链表，求进入环中的第一个节点也就转换成了求两个单链表相交的第一个节点。参考代码如下：

# 已知一个单链表中存在环，求进入环中的第一个节点
def getFirstNodeInCircle(head):

    fast = head
    slow = head

    while fast.next is not None and fast is not None:
        fast = fast.next.next
        slow = slow.next
        if slow == fast:
            break

    fox = slow
    p1 = head
    p2 = fox.next


    node1 = p1
    len1 = 1
    node2 = p2
    len2 = 1

    while node1 != fox:
        node1 = node1.next
        len1 += 1

    while node2 != fox:
        node2 = node2.next
        len2 += 1

    if len1 < len2:
        k = len1 - len2
        while k > 0:
            len1 = len1.next
            k -= 1
    else:
        k = len2 - len1
        while k > 0:
            len2 = len2.next
            k -= 1

    while node1 != node2:
        node1 = node1.next
        node2 = node2.next

    return node1

 

二叉树经典题目

https://blog.csdn.net/lsjseu/article/details/10907037

这东西理解起来费劲，弄几个简单的题目，剩下的可以看链接

class Binary_Tree_Node():
    def __init__(self,root=None, left=None,right=None):
        self.root = root
        self.left_tree = left
        self.right_tree = right

1. 求二叉树中的节点个数
递归解法：
（1）如果二叉树为空，节点个数为0
（2）如果二叉树不为空，二叉树节点个数 = 左子树节点个数 + 右子树节点个数 + 1

# 节点个数
def getNodeNum(root):
    if root is None:
        return 0
    return getNodeNum(root.left_tree) + getNodeNum(root.right_tree) + 1

2. 求二叉树的深度
递归解法：
（1）如果二叉树为空，二叉树的深度为0
（2）如果二叉树不为空，二叉树的深度 = max(左子树深度， 右子树深度) + 1

# 计算二叉树和
def getSum(pRoot):
    if pRoot is None:
        return 0
    return getSum(pRoot.left_tree) + getSum(pRoot.right_tree) + pRoot.root

# 深度
def getDepthNum(root):
    if root is None:
        return 0

    left_d = getDepthNum(root.left_tree)
    right_d = getDepthNum(root.right_tree)

    return (left_d + 1) if left_d > right_d else (right_d + 1)

3. 前序遍历，中序遍历，后序遍历
前序遍历递归解法：
（1）如果二叉树为空，空操作
（2）如果二叉树不为空，访问根节点，前序遍历左子树，前序遍历右子树
参考代码如下：

# 前序
def preTravel(pRoot):
    if pRoot is None:
        return
    print(pRoot.root)
    preTravel(pRoot.left_tree)
    preTravel(pRoot.right_tree)

# 中序
def midTravel(pRoot):
    if pRoot is None:
        return
    preTravel(pRoot.left_tree)
    print(pRoot.root)
    preTravel(pRoot.right_tree)

# 后续
def backTravel(pRoot):
    if pRoot is None:
        return
    preTravel(pRoot.left_tree)
    preTravel(pRoot.right_tree)
    print(pRoot.root)

4.分层遍历二叉树（按层次从上往下，从左往右）

相当于广度优先搜索，使用队列实现。队列初始化，将根节点压入队列。当队列不为空，进行如下操作：弹出一个节点，访问，若左子节点或右子节点不为空，将其压入队列。

# 广度遍历
def widthTravel(pRoot):

    if pRoot is None:
        return
    queue = [pRoot]

    while queue:
        node = queue.pop(0)
        print(node.root)
        if node.left_tree is not None:
            queue.append(node.left_tree)
        if node.right_tree is not None:
            queue.append(node.right_tree)
    return

5. 求二叉树第K层的节点个数
递归解法：
（1）如果二叉树为空或者k<1返回0
（2）如果二叉树不为空并且k==1，返回1
（3）如果二叉树不为空且k>1，返回左子树中k-1层的节点个数与右子树k-1层节点个数之和
参考代码如下：

# 二叉树第k层节点个数
def getNodeNumWithLevel(pRoot, k):
    if k is None and k < 1:
        return 0
    if k == 1:
        return 1
    left = getNodeNumWithLevel(pRoot.left_tree, k-1)
    right = getNodeNumWithLevel(pRoot.right_tree, k-1)
    return left + right

6. 求二叉树中叶子节点的个数
递归解法：
（1）如果二叉树为空，返回0
（2）如果二叉树不为空且左右子树为空，返回1
（3）如果二叉树不为空，且左右子树不同时为空，返回左子树中叶子节点个数加上右子树中叶子节点个数
参考代码如下：

# 二叉树中叶子节点个数
def getLeafNodeNum(pRoot, k):
    if pRoot is None:
        return 0
    if pRoot.left_tree is None and pRoot.right_tree is None:
        return 1

    left = getLeafNodeNum(pRoot.left_tree)
    right = getLeafNodeNum(pRoot.right_tree)
    return left+right

7. 判断两棵二叉树是否结构相同
不考虑数据内容。结构相同意味着对应的左子树和对应的右子树都结构相同。
递归解法：
（1）如果两棵二叉树都为空，返回真
（2）如果两棵二叉树一棵为空，另一棵不为空，返回假
（3）如果两棵二叉树都不为空，如果对应的左子树和右子树都同构返回真，其他返回假
参考代码如下

# 判断两个二叉树结构是否相同
def sameTreeStruct(pRoot1, pRoot2):
    if pRoot1 is None and pRoot2 is None:
        return True
    elif pRoot1 is None or pRoot2 is None:
        return False
    else:
        left = sameTreeStruct(pRoot1.left_tree, pRoot2.left_tree)
        right = sameTreeStruct(pRoot1.right_tree, pRoot2.right_tree)
        return left and right

8. 求二叉树的镜像
递归解法：
（1）如果二叉树为空，返回空
（2）如果二叉树不为空，求左子树和右子树的镜像，然后交换左子树和右子树

# 求二叉树的镜像
def mirror(pRoot):
    if pRoot is None:
        return
    left = mirror(pRoot.left_tree)
    right = mirror(pRoot.right_tree)
    pRoot.left_tree = right
    pRoot.right_tree = left
    return pRoot