机器学习实战笔记-朴素贝叶斯
4.1.基于贝叶斯决策理论的分类方法
朴素贝叶斯
优点:在数据较少的情况下仍然有效,可以处理多类别问题。
缺点:对于输入数据的准备方式较为敏感。
适用数据类型:标称型数据。
朴素贝叶斯是贝叶斯决策理论的一部分,所以讲述朴素负叶斯之前有必要快速了解一下贝叶斯决策理论。
假设现在我们有一个数据集,它由两类数据组成,数据分布如图4-1所示。
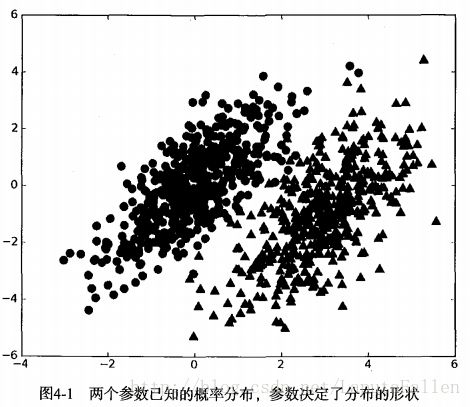
我们现在用 p1(x,y) 表示数据点 (x,y) 属于类别1(图中用圆点表示的类别)的概率,用 p2(x,y) 表示数据点 (x,y) 属于类别2 ( 图中用三角形表示的类别)的概率,那么对于一个新数据点 (x,y) ,可以用下面的规则来判断它的类别:
如果 p1(x,y)>p2(x,y) , 那么类别为1。
如果 p2(x,y)>p1(x,y) , 那么类别为2。
也就是说,我们会选择高概率对应的类别。这就是贝叶斯决策理论的核心思想,即选择具有最高概率的决策。
如果该图中的整个数据使用2个浮点数来表示,并且计算类别概率的python代码只有两行,那么你会更倾向于使用下面哪种方法来对该数据点进行分类?
(1)使用第1章的kNN,进行1000次距离计算;
(2)使用第2章的决策树,分别沿x轴 、y轴划分数据;
(3)计算数据点属于每个类别的概率,并进行比较。
使用决策树不会非常成功;而和简单的概率计算相比,kNN的计算量太大。因此,对于上述问题,最佳选择是使用刚才提到的概率比较方法。
4.2.条件概率
条件概率公式:
贝叶斯准则,告诉我们如何交换条件概率中的条件与结果。即如果已知 p(x|c) ,求 p(c|x) ,那么:
4.3使用条件概率来分类
4.1节提到贝叶斯决策理论要求计算两个概率 p1(x,y) 和 p2(x,y) :
如果 p1(x,y) > p2(x,y) , 那么属于类别1;
如果 p2(x,y) > p1(x,y) , 那么属于类别2。
但这两个准则并不是贝叶斯决策理论的所有内容。用 p1(x,y) 和 p2(x,y) 只是为了尽可能简化描述,而真正需要计算和比较的是 p(c1|x,y) 和 p(c2|x,y) 。这些符号所代表的具体意义是:
给定某个由 (x,y) 表示的数据点,那么该数据点来自类别 c1 的概率是多少?数据点来自类别 c2 的概率又是多少?注意这些概率与刚才给出的概率 p(x,y|c) 并不一样,不过可以使用贝叶斯准则来交换概率中条件与结果。具体地,应用贝叶斯准则得到:
使用这些定义,可以定义贝叶斯分类准则为:
如果 p(c1|x,y) > p(c2|x,y) , 那么属于类别1。
如杲 p(c1|x,y) < p(c2|x,y) , 那么属于类别2。
4.4 使用朴素贝叶斯进行文档分类
机器学习的一个重要应用就是文档的自动分类。在文档分类中,整个文档(如一封电子邮件)是实例,而电子邮件中的某些元素则构成特征。虽然电子邮件是一种会不断增加的文本,但我们同样也可以对新闻报道、用户留言、政府公文等其他任意类型的文本进行分类。我们可以观察文档中出现的词,并把每个词的出现或者不出现作为一个特征,这样得到的特征数目就会跟词汇表中的词目一样多。朴素贝叶斯是上节介绍的贝叶斯分类器的一个扩展,是用于文档分类的常用算法。
朴素贝叶斯的一般过程
⑴ 收 集 数 据 :可以使用任何方法。本章使用RSS源。
(2)准备数据:需要数值型或者布尔型数据。
(3)分析数据:有大量特征时,绘制特征作用不大,此时使用直方图效果更好。
(4)训练算法:计算不同的独立特征的条件概率。
(5)测试算法:计算错误率。
(6)蚀_用算法:一个常见的朴素贝叶斯应用是文档分类。可以在任意的分类场景中使用朴素贝叶斯分类器,不一定非要是文本。
由统计学知,如果每个特征需要 n 个样本,那么对于10个特征将需要 n10 样本,对于包含1000个特征的词汇表将需要 n1000 样本。可以看到,所需要的样本数会随着特征数目增大而迅速增长。
如果特征之间相互独立,那么样本数就可以从 n1000 减少到 n×1000 。所谓独立(independence)指的是统计意义上的独立,即一个特征或者单词出现的可能性与它和其他单词相邻没有关系。举个例子讲,假设单词bacon出现在unhealthy后面与出现在delicious后面的概率相同。当然,我们知道这种假设并不正确,bacon常常出现在delicious附近,而很少出现在unhealthy附近 ,这个假设正是朴素贝叶斯分类器中朴素(naive ) 一词的含义。朴素贝叶斯分类器中的另一个假设是,每个特征同等重要。其实这个假设也有问题。 如果要判断留言板的留言是否得当,那么可能不需要看完所有的1000个单词,而只需要看10~20个特征就足以做出判断了。尽管上述假设存在一些小的瑕疵,但朴素贝叶斯的实际效果却很好。
4.5使用Python进行文本分类
要从文本中获取特征,需要先拆分文本。具体如何做呢?这里的特征是来自文本的词条(token), 一个词条是字符的任意组合。可以把词条想象为单词,也可以使用非单词词条,如URL、IP地址或者任意其他字符串。然后将每一个文本片段表示为一个词条向量,其中值为1表示词条出现在文档中,0表示词条未出现。
以在线社区的留言板为例。为了不影响社区的发展,我们要屏蔽侮辱性的言论,所以要构建一个快速过滤器,如果某条留言使用了负面或者侮辱性的语言,那么就将该留言标识为内容不当。过滤这类内容是一个很常见的需求。对此问题建立两个类别:侮辱类和非侮辱类使用1和0分别表示。
4.5.1
准备数据:从文本中构建词向量
我们将把文本看成单词向量或者词条向量,也就是说将句子转换为向量。考虑出现在所有文档中的所有单词,再决定将哪些词纳人词汇表或者说所要的词汇集合,然后必须要将每一篇文档转换为词汇表上的向量。接下来我们正式开始。打开文本编辑器,创建一个叫base.py的新文件,然后将下面的程序清单添加到文件中。
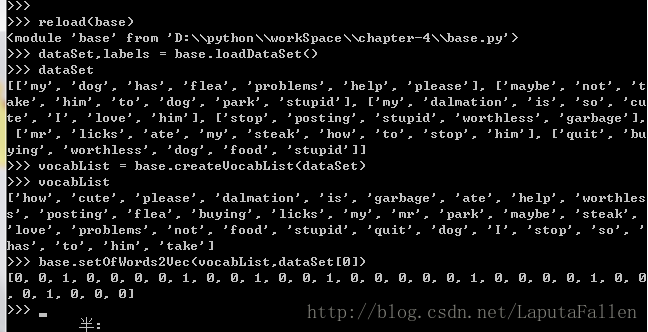
词表到向量的转换函数,代码:
def loadDataSet():
postingList=[[‘my’, ‘dog’, ‘has’, ‘flea’, ‘problems’, ‘help’, ‘please’],
[‘maybe’, ‘not’, ‘take’, ‘him’, ‘to’, ‘dog’, ‘park’, ‘stupid’],
[‘my’, ‘dalmation’, ‘is’, ‘so’, ‘cute’, ‘I’, ‘love’, ‘him’],
[‘stop’, ‘posting’, ‘stupid’, ‘worthless’, ‘garbage’],
[‘mr’, ‘licks’, ‘ate’, ‘my’, ‘steak’, ‘how’, ‘to’, ‘stop’, ‘him’],
[‘quit’, ‘buying’, ‘worthless’, ‘dog’, ‘food’, ‘stupid’]]
classVec = [0,1,0,1,0,1] #1代表侮辱性文字,0代表正常言论
return postingList,classVec
def createVocabList(dataSet):
#创建空set
vocabSet = set([])
#遍历数据集,将删除重复项的每行数据作并集,存到vocabSet中
for document in dataSet:
vocabSet = vocabSet | set(document)
return list(vocabSet)
def setOfWords2Vec(vocabList, inputSet):
#创建与vocabList同等长度的零向量,如[0,0,….]
returnVec = [0] * len(vocabList)
#遍历inputSet,将对应于vocabList相同单词的地方设置为1
for word in inputSet:
if word in vocabList:
returnVec[vocabList.index(word)] = 1
else:
print(“the word %s is not in my Vocabulary!” % word)
return returnVec4.5.2 训练算法:从词向量计算概率
前面介绍了如何将一组单词转换为一组数字,接下来看看如何使用这些数字计算概率。现在已经知道一个词是否出现在一篇文档中,也知道该文档所属的类别。还记得3.2节提到的贝叶斯准则?我们重写贝叶斯准则,将之前的 x、y 替换为 w 。粗体 w 表示这是一个向量,即它由多个数组成。在这个例子中,数值个数与词汇表中的词个数相同。
p(ci|w)=p(w|ci)p(ci)p(w)
我们将使用上述公式,对每个类计算该值,然后比较这两个概率值的大小。如何计算呢?首先可以通过类别 i (侮辱性留言或非侮辱性留言)中文档数除以总的文档数来计算概率 p(ci) 。接下来计算 p(w|ci) , 这里就要用到朴素贝叶斯假设。如果将 w 展开为一个个独立特征,那么就可以将上述概率写作 p(w0,w1....wn|ci) 。这里假设所有词都互相独立,该假设也称作条件独立性假设,它意味着可以使用 p(w0|ci)p(w1|ci)...p(wn|ci) 计算上述概率,这就极大地简化了计算的过程。
该函数的伪代码如下:
计算每个类别中的文档数目
对每篇训练文档:
对每个类别:
如果词条出现文档中―增加该词条的计数值
增加所有词条的计数值
对每个类别:
对每个词条:
将该词条的数目除以总词条数目得到条件概率4回每个类别的条件概率
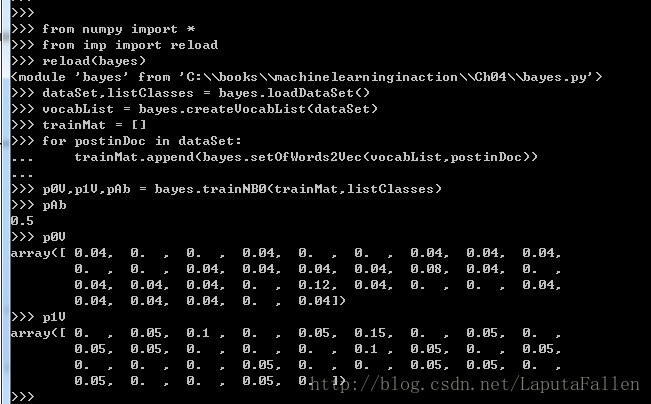
朴素贝叶斯分类器训练函数,代码如下:
def trainNB0(trainMatrix,trainCategory):
#获取文档数量,每个文档为向量形式
numTrainDocs = len(trainMatrix)
numWords = len(trainMatrix[0])
#获取侮辱性文档概率
pAbusive = sum(trainCategory)/float(numTrainDocs)
p0Num = zeros(numWords); p1Num = zeros(numWords)
p0Denom = 0.0; p1Denom = 0.0
for i in range(numTrainDocs):
if trainCategory[i] == 1:
p1Num += trainMatrix[i]
p1Denom += sum(trainMatrix[i])
else:
p0Num += trainMatrix[i]
p0Denom += sum(trainMatrix[i])
p1Vect = p1Num/p1Denom
p0Vect = p0Num/p0Denom
return p0Vect,p1Vect,pAbusive书中代码解读:代码函数中的输人参数为文档矩阵trainMatrix,以及由每篇文档类别标签所构成的向量 trainCategory.首先,计算文档属于侮辱性文档(class=1)的概率,即 p(1) 。因为这是一个二类分类问题,所以可以通过 1−p(1) 得到 p(0) 。对于多于两类的分类问题,则需要对代码稍加修改。
计算 p(wi|c1) 和 p(wi|c0) ,需要初始化程序中的分子变量和分母变量0 。由于 w 中元素如此众多,因此可以使用Numpy数组快速计算这些值。上述程序中的分母变量是一个元素个数等于词汇表大小的Numpy数组。在for循环中,要遍历训练集trainMatrix中的所有文档。一旦某个词语(侮辱性或正常词语)在某一文档中出现,则该词对应的个数(P1Num后者p0Num)就加1,而且在所有的文档中,该文档的总词数也相应加1 ©。对于两个类别都要进行同样的计算处理。
最后,对每个元素除以该类别中的总词数 。利用Numpy可以很好实现,用一个数组除以浮点数即可,若使用常规的python列表则难以完成这种任务
4.5.3 测试算法:根据现实情况修改分类器
利用贝叶斯分类器对文档进行分类时,要计算多个概率的乘积以获得文档属于某个类别的概率,即计算 p(w0|ci)p(w1|ci)...p(wn|ci) 。如果其中一个概率值为0 ,那么最后的乘积也为0。为降低这种影响,可以将所有词的出现数初始化为1,并将分母初始化为2。
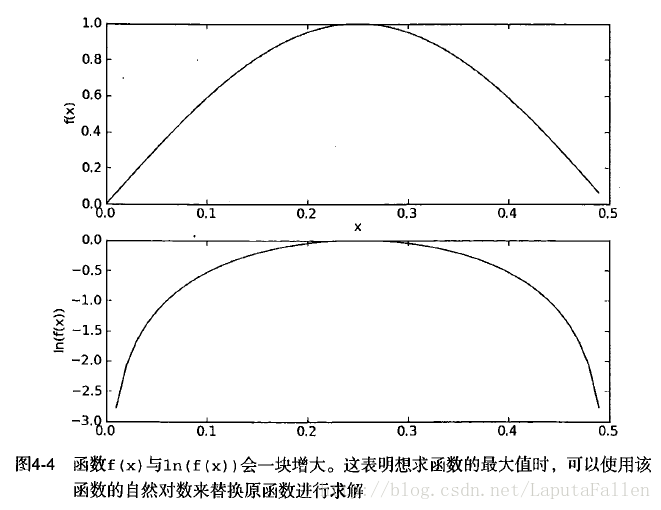
另一个遇到的问题是下溢出,这是由于太多很小的数相乘造成的。当计算乘积 p(w0|ci)p(w1|ci)...p(wn|ci) ,由于大部分因子者3非常小,所以程序会下溢出或者得到不正确的答案。(读者可以python尝试相乘许多很小的数,最后四舍五人后会得到0。)一种解决办法是对乘积取自然对数。在代数中有 ln(a∗b)=ln(a)+ln(b) , 于是通过求对数可以避免下溢出或者浮点数舍入导致的错误。同时,采用自然对数进行处理不会有任何损失。图4-4给出函数 f(x)和ln(f(x)) 的曲线。检查这两条曲线,就会发现它们在相同区域内同时增加或者减少,并且在相同点上取到极值。它们的取值虽然不同,但不影响最终结果。
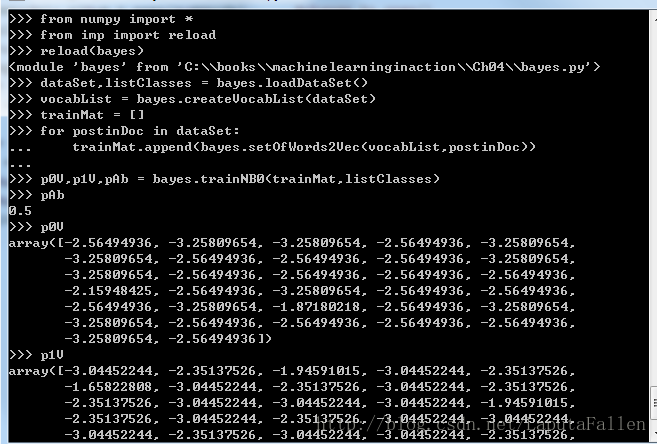
更改后的代码:
def trainNB0(trainMatrix,trainCategory):
#获取文档数量,每个文档为向量形式
numTrainDocs = len(trainMatrix)
numWords = len(trainMatrix[0])
#获取侮辱性文档概率
pAbusive = sum(trainCategory)/float(numTrainDocs)
p0Num = ones(numWords); p1Num = ones(numWords) #change to ones()
p0Denom = 2.0; p1Denom = 2.0 #change to 2.0
for i in range(numTrainDocs):
if trainCategory[i] == 1:
p1Num += trainMatrix[i]
p1Denom += sum(trainMatrix[i])
else:
p0Num += trainMatrix[i]
p0Denom += sum(trainMatrix[i])
p1Vect = log(p1Num/p1Denom) #change to log()
p0Vect = log(p0Num/p0Denom) #change to log()
return p0Vect,p1Vect,pAbusive朴素贝叶斯分类函数,代码如下:
def classifyNB(vec2Classify, p0Vec, p1Vec, pClass1):
p1 = sum(vec2Classify * p1Vec) + log(pClass1) #element-wise mult
p0 = sum(vec2Classify * p0Vec) + log(1.0 - pClass1)
if p1 > p0:
return 1
else:
return 0
def testingNB():
listOPosts,listClasses = loadDataSet()
myVocabList = createVocabList(listOPosts)
trainMat=[]
for postinDoc in listOPosts:
trainMat.append(setOfWords2Vec(myVocabList, postinDoc))
p0V,p1V,pAb = trainNB0(array(trainMat),array(listClasses))
testEntry = ['love', 'my', 'dalmation']
thisDoc = array(setOfWords2Vec(myVocabList, testEntry))
print(testEntry,'classified as: ',classifyNB(thisDoc,p0V,p1V,pAb))
testEntry = ['stupid', 'garbage']
thisDoc = array(setOfWords2Vec(myVocabList, testEntry))
print(testEntry,'classified as: ',classifyNB(thisDoc,p0V,p1V,pAb))书中的代码解释,4个输入:要分类的向量vec2Classify以及使用函数trainNB0( )计算得到的三个概率。使用NumPy的数组来计算两个向量相乘的结果0 。这里的相乘是指对应元素相乘,即先将两个向量中的第1个元素相乘,然后将第2个元素相乘,以此类推。接下来将词汇表中所有词的对应值相加,然后将该值加到类别的对数概率上。最后,比较类别的概率返回大概率对应的类别标签
4.5.4 准备数据:文档词袋模型
目前为止,我们将每个词的出现与否作为一个特征,这可以被描述为词集模型(set-of-words model)。如果一个词在文档中出现不止一次,这可能意味着包含该词是否出现在文档中所不能表达的某种信息,这种方法被称为词袋模型(bag-of-words model)。在词袋中,每个单词可以出现多次,而在词集中,每个词只能出现一次。为适应词袋模型,需要对函数setOfWords2Vec()稍加修改,修改后的函数称为bagOfWords2Vec()。
代码如下:
def bagOfWords2VecMN(vocabList, inputSet):
returnVec = [0]*len(vocabList)
for word in inputSet:
if word in vocabList:
returnVec[vocabList.index(word)] += 1
return returnVec4.6 示例:使用朴素贝叶斯过滤垃圾邮件
在前面那个简单的例子中,我们引人了字符串列表。使用朴素贝叶斯解决一些现实生活中的问题时,需要先从文本内容得到字符串列表,然后生成词向量。下面这个例子中,.我们将了解朴素贝叶斯的一个最著名的应用:电子邮件垃圾过滤。
示例:使用朴素贝叶斯对电子邮件进行分类;
(1)收集数据:提供文本文件。
(2)准备数据:将文本文件解析成词条向量。
(3)分析数据:检查词条确保解析的正确性。
(4)训练算法:使用我们之前建立的trainNB0()函数。
(5)测试算法:使用classifyNB(),并且构建一个新的测试函数来计算文档集的错误率。
(6)使用算法:构建一个完整的程序对一组文档进行分类,将错分的文档输出到屏幕上。
4 . 6 . 1 准备数据:切分文本
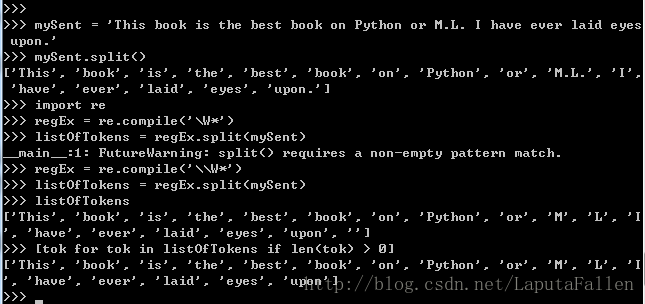
可以看到,大多是使用字符串内置的split()方法,正则表达式,以及列表推导来处理切分文本。
4.6.2 测试算法:使用朴素贝叶斯进行交叉验证
文件解析及完整的垃圾邮件测试函数,代码如下:
def textParse(bigString): #input is big string, #output is word list
import re
comp = re.compile('\\W*')
listOfTokens = comp.split(bigString)
return [tok.lower() for tok in listOfTokens if len(tok) > 2]
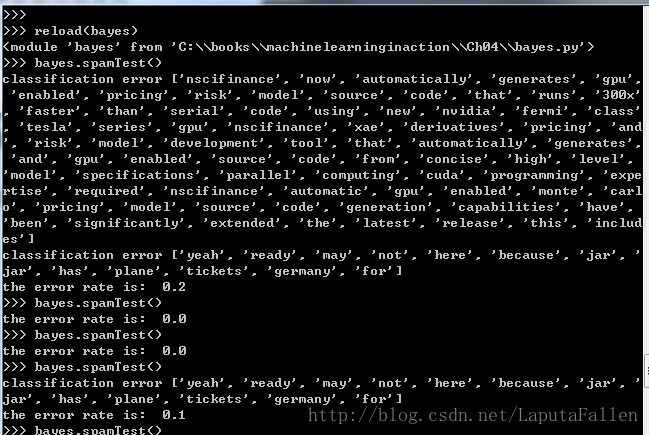
def spamTest():
docList=[]; classList = []; fullText =[]
#读取所有50封邮件
for i in range(1,26):
path = 'email/spam/' + str(i) + ".txt"
#python3得已rb形式打开文件读取
temp = str(open(path,'rb').read())
wordList = textParse(temp)
docList.append(wordList)
#fullText.extend(wordList) 不知道书中这行代码有什么意义
classList.append(1)
path = 'email/ham/' + str(i) + ".txt"
temp = str(open(path,'rb').read())
wordList = textParse(temp)
docList.append(wordList)
#fullText.extend(wordList)
classList.append(0)
vocabList = createVocabList(docList)#create vocabulary
trainingSet = list(range(50)); testSet=[] #create test set
for i in range(10):
randIndex = int(random.uniform(0,len(trainingSet)))
testSet.append(trainingSet[randIndex])
del(trainingSet[randIndex])
trainMat=[]; trainClasses = []
for docIndex in trainingSet:#train the classifier (get probs) trainNB0
trainMat.append(bagOfWords2VecMN(vocabList, docList[docIndex]))
trainClasses.append(classList[docIndex])
p0V,p1V,pSpam = trainNB0(array(trainMat),array(trainClasses))
errorCount = 0
for docIndex in testSet: #classify the remaining items
wordVector = bagOfWords2VecMN(vocabList, docList[docIndex])
if classifyNB(array(wordVector),p0V,p1V,pSpam) != classList[docIndex]:
errorCount += 1
print("classification error",docList[docIndex])
print('the error rate is: ',float(errorCount)/len(testSet))
#return vocabList,fullText书中代码解读如下(非常详细):
第一个函数textParse()接受一个大字符串并将其解析为字符串列表。该函数去掉少于两个字符的字符串,并将所有字符串转换为小写。你可以在函数中添加更多的解析操作,但是目前的实现对于我们的应用足够了。
第二个函数spamTest()对贝叶斯垃圾邮件分类器进行自动化处理。导人文件夹spam与ham下的文本文件,并将它们解析为词列表0 。接下来构建一个测试集与一个训练集,两个集合中的邮件都是随机选出的。本例中共有50封电子邮件,并不是很多,其中的10封电子邮件被随机选择为测试集。分类器所需要的概率计算只利用训练集中的文档来完成。Python变量trainingSet是一个整数列表,其中的值从0到49。接下来,随机选择其中10个文件©。选择出的数字所对应的文档被添加到测试集,同时也将其从训练集中剔除。这种随机选择数据的一部分作为训练集,而剩余部分作为测试集的过程称为留存交叉验证(hold-out cross validation)。假定现在只完成了一次迭代,那么为了更精确地估计分类器的错误率,就应该进行多次迭代后求出平均错误率。
接下来的for循环遍历训练集的所有文档,对每封邮件基于词汇表并使用setOfWords2Vec()函数来构建词向量。这些词在trainNB0( ) 函数中用于计算分类所需的概率。然后遍历测试集,对其中每封电子邮件进行分类 。如果邮件分类错误,则错误数加1,最后给出总的错误百分比。
4.7示例:使用朴素贝叶斯分类器从个人广告中获取区域倾向
在这个最后的例子当中,我们将分别从美国的两个城市中选取一些人,通过分析这些人发布的征婚广告信息,来比较这两个城市的人们在广告用词上是否不同。如果结论确实是不同,那么他们各自常用的词是哪些?从人们的用词当中,我们能否对不同城市的人所关心的内容有所了解?
示例:使用朴素贝叶斯来发现地域相关的用词
⑴收集数据:从RSS源收集内容,这里需要对RSS源构建一个接口。
(2)准备数据:将文本文件解析成词条向量。
(3)分析数据:检查词条确保解析的正确性。
(4)训练算法:使用我们之前建立的trainNB0()函数。
(5)测试算法:观察错误率,确保分类器可用。可以修改切分程序,以降低错误率,提高分类结果。
(6)使用算法:构建一个完整的程序,封装所有内容。给定两个RSS源,该程序会显示最常用的公共词。
4.7.1 收集数据:导入RSS源
RSS源分类器及髙频词去除函数,代码如下:
def calcMostFreq(vocabList,fullText):
import operator
freqDict = {}
for token in vocabList:
freqDict[token]=fullText.count(token)
sortedFreq = sorted(freqDict.iteritems(), key=operator.itemgetter(1), reverse=True)
return sortedFreq[:30]
def localWords(feed1,feed0):
import feedparser
docList=[]; classList = []; fullText =[]
minLen = min(len(feed1['entries']),len(feed0['entries']))
for i in range(minLen):
wordList = textParse(feed1['entries'][i]['summary'])
docList.append(wordList)
fullText.extend(wordList)
classList.append(1) #NY is class 1
wordList = textParse(feed0['entries'][i]['summary'])
docList.append(wordList)
fullText.extend(wordList)
classList.append(0)
vocabList = createVocabList(docList)#create vocabulary
top30Words = calcMostFreq(vocabList,fullText) #remove top 30 words
for pairW in top30Words:
if pairW[0] in vocabList: vocabList.remove(pairW[0])
trainingSet = range(2*minLen); testSet=[] #create test set
for i in range(20):
randIndex = int(random.uniform(0,len(trainingSet)))
testSet.append(trainingSet[randIndex])
del(trainingSet[randIndex])
trainMat=[]; trainClasses = []
for docIndex in trainingSet:#train the classifier (get probs) trainNB0
trainMat.append(bagOfWords2VecMN(vocabList, docList[docIndex]))
trainClasses.append(classList[docIndex])
p0V,p1V,pSpam = trainNB0(array(trainMat),array(trainClasses))
errorCount = 0
for docIndex in testSet: #classify the remaining items
wordVector = bagOfWords2VecMN(vocabList, docList[docIndex])
if classifyNB(array(wordVector),p0V,p1V,pSpam) != classList[docIndex]:
errorCount += 1
print('the error rate is: ',float(errorCount)/len(testSet))
return vocabList,p0V,p1V书中代码解读:
代码中引人了一个辅助函数calcMostFreq()。该函数遍历词汇表中的每个词并统计它在文本中出现的次数,然后根据出现次数从高到低对词典进行排序,最后返回排序最高的100个单词。你很快就会明白这个函数的重要性。
下一个函数localWords( )使用两个RSS源作为参数。RSS源要在函数外导人,这样做的原因是RSS源会随时间而改变。如果想通过改变代码来比较程序执行的差异,就应该使用相同的输入。重新加载RSS源就会得到新的数据,但很难确定是代码原因还是输人原因导致输出结果的改变。函数localWords与程序清单4-5中的spamTest()函数几乎相同,区别在于这里访问的是RSS源而不是文件。然后调用函数calcMostFreq ( )来获得排序最高的100个单词并随后将它们移除 。函数的剩余部分spamTest( ) 基本类似,不同的是最后一行要返回下面要用到的值。
你可以注释掉用于移除高频词的三行代码,然后比较注释前后的分类性能。我自己也尝试了一下,去掉这几行代码之后,我发现错误率为5 4 %,而保留这些代码得到的错误率为70。这里观察到的一个有趣现象是,这些留言中出现次数最多的前30个词涵盖了所有用词的30%。我在进行测试的时候,vocabList的大小约为3000个词。也就是说,词汇表中的一小部分单词却占据了所有文本用词的一大部分。产生这种现象的原因是因为语言中大部分都是冗余和结构辅助性内容。另一个常用的方法是不仅移除高频词,同时从某个预定词表中移除结构上的辅助词。该词表称为停用词表(stop word list),目前可以找到许多停用词表(在本书写作期间,http://www.ranks.nUresources/stopwords.html上有一个很好的多语言停用词列表)。
4.7.2 分析数据:显示地域相关的用词
可以先对向量pSF与pNY进行排序,然后按照顺序将词打印出来。下面的最后一段代码会完成这部分工作
最具表征性的词汇显示函数,代码如下:
def getTopWords(ny,sf):
import operator
vocabList,p0V,p1V=localWords(ny,sf)
#元组数组,元祖中元素为单词和对应的频率
topNY=[]; topSF=[]
for i in range(len(p0V)):
if p0V[i] > -6.0 : topSF.append((vocabList[i],p0V[i]))
if p1V[i] > -6.0 : topNY.append((vocabList[i],p1V[i]))
sortedSF = sorted(topSF, key=lambda pair: pair[1], reverse=True)
print("SF**SF**SF**SF**SF**SF**SF**SF**SF**SF**SF**SF**SF**SF**SF**SF**")
for item in sortedSF:
print(item[0])
sortedNY = sorted(topNY, key=lambda pair: pair[1], reverse=True)
print("NY**NY**NY**NY**NY**NY**NY**NY**NY**NY**NY**NY**NY**NY**NY**NY**")
for item in sortedNY:
print(item[0])最后输出的单词很有意思。值得注意的现象是,程序输出了大量的停用词。移除固定的停用词看看结果会如何变化也十分有趣。依我的经验来看,这样做的话,分类错误率也会降低。