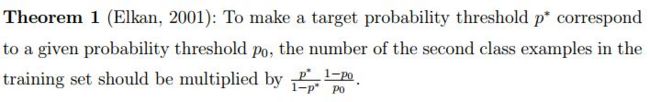《机器学习》周志华西瓜书习题参考答案：第3章 - 线性模型

【机器学习】《机器学习》周志华西瓜书 笔记/习题答案 总目录

• https://blog.csdn.net/TeFuirnever/article/details/96178919

——————————————————————————————————————————————————————

• 【机器学习】《机器学习》周志华西瓜书读书笔记：第3章 - 线性模型

习题

• 试想一下，拟合曲线时，如果不考虑偏置项，则只能拟合一条过原点的曲线。在多元线性回归中也同理，如果不考虑偏置项，那么拟合的超平面就只能过原点，但现实中数据点的分布并不是这样的。使用一个不依赖于属性的的偏置项能够让权重向量所描述的超平面更好地拟合数据点的分布。如果输出值的期望（均值）为0就不需要考虑偏置项了，或者说偏置项此时就等于0。

• 或者可以用变量归一化（max-min或z-score）来消除偏置。

• 再或者可以用任意两个线性模型实例进行相减，以此消除了偏置，然后对新的样本做线性回归，只需要用模型 $y=w^{t}x$。

式1：$y=\frac{1}{1+e^{-({\mathbf{w}}^{\mathbf{T}}\mathbf{x}+b)}}$

式2：$E(\beta )={\sum }_{i=1}^m(-y_i{\beta }^T\widehat{x_i}+\ln (1+e^{{\beta }^T\widehat{{\mathbf{x}}_{\mathbf{i}}}}))$

一种方法 笔记中已经提到了，检验一个函数是否凸函数，可以看其二阶导数是否在区间上恒大于0。

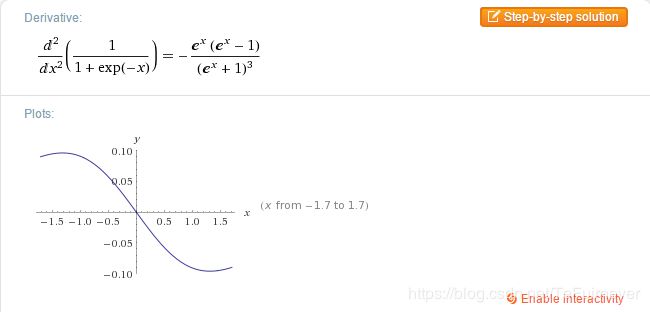
目标函数（也即sigmoid函数）：

显然，sigmoid的二阶导数在自变量大于0处取值小于0，所以它不是凸函数。

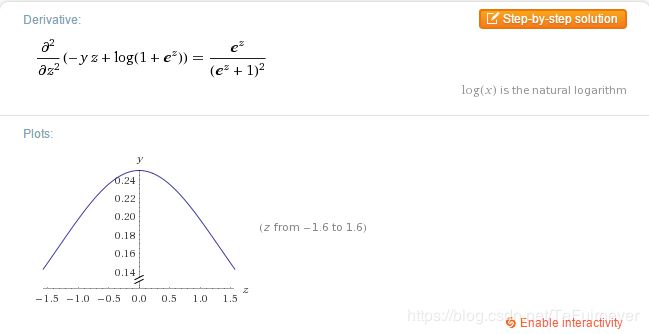
对数似然函数：

可以看到这个函数在区间上恒大于0（两边无限延伸），符合凸函数的要求。

另一种证明方法是利用 如果一个多元函数是凸的，那么它的Hessian矩阵是半正定的。

对于式1，这里 $y$ 理解为标量，而 $x$ 为 $X$ 的列向量。

则其一阶导：

$$\frac{\partial y}{\partial w}=x\left(y-y^2\right)$$

其二阶导：

$$\frac{{\partial }^{2}y}{\partial w\partial w^T}=x{x}^{T}y(1-y)(1-2y)$$（即海森矩阵)

其中 $x{x}^T$ 秩为1，非零特征值只有一个，其正负号取决于 $y(1-y)(1-2y)$ ，显然当在(0,1)之间变化时，特征值正负号会发生变化，于是式1关于 $w$ 的海森矩阵非半正定，因此非凸。

对于式2，关于 $\beta$ 的二阶导有 （原书p60）

$$\frac{{\partial }^{2}l(\beta )}{\partial \beta \partial {\beta }^T}=\sum _{i=1}^m{\tilde{x}}_i{\tilde{x}}_i^T{p}_1\left({\tilde{x}}_i;\beta \right)(1-p_1\left({\tilde{x}}_i\right))=XP{X}^T$$

其中第一个等号是原书中的，第二个等号中 $X$ 为 $(n,m)$ 矩阵，每一列对应一个样本，$P$ 为对角矩阵，$P_{ii}=p_1\left(\widetilde{x_i};\beta \right)\left(1-p_1\left(\widetilde{x_i}\right)\right)$ 。

关于 $XP{X}^T$ ，对于任意向量 $z$ 都有：

$$z^{T}XP{X}^{T}z={\left(X^{T}z\right)}^{T}P\left(X^{T}z\right)=v^{T}Pv=\sum _i{P}_{ii}{v}_i^2\ge 0$$

因此其海森矩阵为半正定。

西瓜数据集3.0α：

编号	密度	含糖率	好瓜
1	0.697	0.460	是
2	0.774	0.376	是
3	0.634	0.264	是
4	0.608	0.318	是
5	0.556	0.215	是
6	0.403	0.237	是
7	0.481	0.149	是
8	0.437	0.211	是
9	0.666	0.091	否
10	0.243	0.0267	否
11	0.245	0.057	否
12	0.343	0.099	否
13	0.639	0.161	否
14	0.657	0.198	否
15	0.36	0.37	否
16	0.593	0.042	否
17	0.719	0.103	否

把这个数据集转换为csv表格，并且注意要把 标记转换为0、1，注意不是-1、+1！！逻辑回归的二分类标记必须是0、1，对应于sigmoid函数的值域。

代码：

%matplotlib inline
import numpy as np
import pandas as pd  
from matplotlib import pyplot as plt 
from mpl_toolkits.mplot3d import Axes3D

#读入csv文件数据 
df = pd.read_csv('../watermelon3.0alpha.csv')
df['intercept'] = 1.0  
df

dataMat = np.array(df[['density','Sugar_content','intercept']].values[:,:])

labelMat = np.mat(df['label'].values[:]).transpose()

def sigmoid(z):  
    return 1.0 / (1 + np.exp(-z))

def LogisticRegression(dataMat,labelMat):  
    m,n = np.shape(dataMat)  
    alpha = 0.05       # 步长
    iterations = 2000  # 最大迭代次数
    weights = np.array(np.array(np.ones((n,1))))  # 初始权重
    
    # 用梯度上升法更新权重
    for k in range(iterations):    
        z = np.dot(dataMat,weights)        
        error = labelMat - sigmoid(z)            
        weights = weights + alpha * np.dot(dataMat.transpose(),error)  
        
    return weights

def DrawResult(weights):  
    m = np.shape(dataMat)[0]  
    xcord1, ycord1, zcord1= [], [], []
    xcord2, ycord2, zcord2= [], [], []
    xcord3, ycord3, zcord3= [], [], []
    xcord4, ycord4, zcord4= [], [], []
    
    # 按照类别划分数据点
    for i in range(m):  
        if labelMat[i]==1:  
            z = sigmoid(dataMat[i, :] * weights)
            if z>= 0.5:
                xcord1.append(dataMat[i, 0])  
                ycord1.append(dataMat[i, 1]) 
                zcord1.append(z)
            else:
                xcord2.append(dataMat[i, 0])  
                ycord2.append(dataMat[i, 1]) 
                zcord2.append(z)
        else:  
            z = sigmoid(dataMat[i, :] * weights)
            if z< 0.5:
                xcord3.append(dataMat[i, 0])  
                ycord3.append(dataMat[i, 1]) 
                zcord3.append(z)
            else:
                xcord4.append(dataMat[i, 0])  
                ycord4.append(dataMat[i, 1]) 
                zcord4.append(z)
    
    # 创建三维图表
    fig = plt.figure()  
    ax = Axes3D(fig)
    
    # 画出判决平面
    x = np.arange(0.2, 1.0, 0.1)
    y = np.arange(0.0, 0.6, 0.1)
    X, Y = np.meshgrid(x, y)
    z = np.array([0.5 for x,y in zip(np.ravel(X), np.ravel(Y))])
    Z = z.reshape(X.shape)    
    ax.plot_surface(X, Y, Z, rstride=10, cstride=10, color=(0, 0.6, 0.6, 0.1))
    
    # 按类别画出数据点
    ax.scatter(xcord1, ycord1, zcord1, s=30, c='red') 
    ax.scatter(xcord2, ycord2, zcord2, s=30, c='red', marker='x')  
    ax.scatter(xcord3, ycord3, zcord3, s=30, c='green') 
    ax.scatter(xcord4, ycord4, zcord4, s=30, c='green', marker='x')  
    
    ax.set_xlim(0.0, 1.0)
    ax.set_ylim(-0.1, 0.7)
    ax.set_zlim(-0.2, 1.2)
    ax.set_xlabel('density')  
    ax.set_ylabel('Sugar content')
    ax.set_zlabel('Logit')
    plt.title('Gradient ascent logistic regression')
    plt.show()

weights = LogisticRegression(dataMat, labelMat)

DrawResult(weights)

用了梯度上升法来更新权值，步长0.05，最大迭代次数2000次。上图中红色为好瓜，绿色为坏瓜，圆形标记表示预测正确，叉号标记表示预测错误。可以看到有一个好瓜被预测为坏瓜，有两个坏瓜被预测为好瓜。事实上，在200次迭代后，已经基本定型了，权值并没有太大的变化。

参考博客——https://blog.csdn.net/snoopy_yuan/article/details/64131129

参考博客——https://blog.csdn.net/snoopy_yuan/article/details/64443841

给出两种思路：

• 参考书p57，采用广义线性模型，如 y-> ln(y)。
• 参考书p137，采用核方法将非线性特征空间隐式映射到线性空间，得到KLDA（核线性判别分析）。

原书对很多地方解释没有解释清楚，把原论文看了一下《Solving Multiclass Learning Problems via Error-Correcting Output Codes》。

先把几个涉及到的理论解释一下。

首先原书中提到：

对同等长度的编码，理论上来说，任意两个类别之间的编码距离越远，则纠错能力越强。因此，在码长较小时可根据这个原则计算出理论最优编码。

其实这一点在论文中也提到，“假设任意两个类别之间最小的海明距离为 $d$，那么此纠错输出码最少能矫正 $\left[\frac{d-1}{2}\right]$ 位的错误。

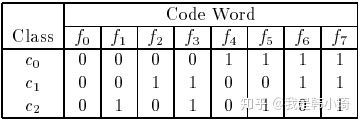
拿上图论文中的例子解释一下，上图中，所有类别之间的海明距离都为4，假设一个样本正确的类别为 $c1$ ，那么codeword应该为 ‘0 0 1 1 0 0 1 1’，若此时有一个分类器输出错误，变成‘0 0 0 1 0 0 1 1’，那么此时距离最近的仍然为 $c1$，若有两个分类输出错误如‘0 0 0 0 0 0 1 1’，此时与 $c1,c2$ 的海明距离都为2，无法正确分类。即任意一个分类器将样本分类错误，最终结果依然正确，但如果有两个以上的分类器错误，结果就不一定正确了。这是 $\left[\frac{d-1}{2}\right]$ 的由来。

此外，原论文中提到，一个好的纠错输出码应该满足两个条件：

• 行分离。任意两个类别之间的codeword距离应该足够大。
• 列分离。任意两个分类器 $f_i,f_j$ 的输出应相互独立，无关联。这一点可以通过使分类器 $f_i$ 编码与其他分类编码的海明距离足够大实现，且与其他分类编码的反码的海明距离也足够大（有点绕）。

第一点其实就是原书提到的，已经解释过了，说说第二点：

如果两个分类器的编码类似或者完全一致，很多算法（比如C4.5）会有相同或者类似的错误分类，如果这种同时发生的错误过多，会导致纠错输出码失效。（翻译原论文）

个人理解就是：若增加两个类似的编码，那么当误分类时，就从原来的1变成3，导致与真实类别的codeword海明距离增长。极端情况，假设增加两个相同的编码，此时任意两个类别之间最小的海明距离不会变化依然为 $d$ ，而纠错输出码输出的codeword与真实类别的codeword的海明距离激增（从1变成3）。所以如果有过多同时发出的错误分类，会导致纠错输出码失效。

另外，两个分类器的编码也不应该互为反码，因为很多算法（比如C4.5，逻辑回归）对待0-1分类其实是对称的，即将0-1类互换，最终训练出的模型是一样的。也就是说两个编码互为补码的分类器是会同时犯错的。同样也会导致纠错输出码失效。

当然当类别较少时，很难满足上面这些条件。如上图中，一共有三类，那么只有 $2^3=8$ 中可能的分类器编码（ $f_0-f7$），其中后四种（ $f_4-f_7$ ）是前四种的反码，都应去除，再去掉全为0的 $f_0$，就只剩下三种编码选择了，所以很难满足上述的条件。事实上，对于 $k$ 种类别的分类，再去除反码和全是0或者1的编码后，就剩下 $2^k-1$ 中可行的编码。

原论文中给出了构造编码的几种方法。其中一个是：

回到题目上，在类别为4时，其可行的编码有7种，按照上述方法有：

当码长为9时，那么 $f_6$ 之后加任意两个编码，即为最优编码，因为此时再加任意的编码都是先有编码的反码，此时，类别之间最小的海明距离都为4，不会再增加。

条件分解为两个：一是出错的概率相当，二是出错的可能性相互独立。

先看第一个把，其实就是每个一位上的分类器的泛化误差相同，要满足这个条件其实取决于样本之间的区分难度，若两个类别本身就十分相似，即越难区分，训练出的分类器出错的概率越大，原书p66也提到：

将多个类拆解为两个"类别子集“，所形成的两个类别子集的区分难度往往不同，即其导致的二分类问题的难度不同。
所以每个编码拆解后类别之间的差异越相同（区分难度相当），则满足此条件的可能性越大。在实际中其实很难满足。

第二个，相互独立。在3.7中也提到过，原论文中也提出一个好的纠错输出码应该满足的其中一个条件就是各个位上分类器相互独立，当类别越多时，满足这个条件的可能性越大，在3.7中也解释了当类别较少时，很难满足这个条件。

至于产生的影响。西瓜书上也提到：

一个理论纠错牲质很好、但导致的三分类问题较难的编码，与另一个理论纠错性质差一些、但导致的二分类问题较简单的编码，最终产生的模型性能孰强孰弱很难说。

因为OvR或者MvM在输出结果阶段，是对各个二分类器的结果进行汇总，汇总的这个过程就会消除不平衡带来的影响（因为总和总是1）

p66 其实已经给出答案了：

对 OvR 、 MvM 来说，由于对每个类进行了相同的处理，其拆解出的二分类任务中类别不平衡的影响会相互抵消，因此通常不需专门处理.

这道题目其实是周志华教授的一篇论文《On Multi-Class Cost-Sensitive Learning》。把论文理论部分读了一遍。现在尝试概述一遍吧。

首先说一点关于“再缩放”的个人理解：无论是代价敏感学习还是非代价敏感学习中，“再缩放”各种方法（过采样、欠采样、阈值移动等）都是在调整各类别对模型的影响程度，即各类别的权重。

方程组有解。

其伴随矩阵秩小于c。

参考文章

• 机器学习（周志华）课后习题
• https://blog.csdn.net/snoopy_yuan/article/category/6788615