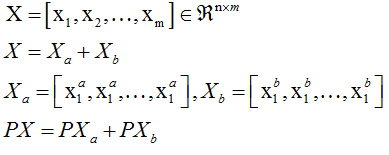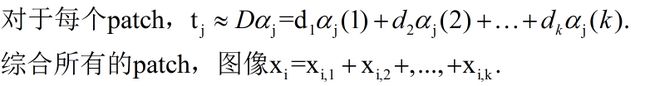稀疏表示+子空间学习 （ICCV2011）

http://blog.csdn.net/yihaizhiyan/article/details/7633658

解读文献：L. Zhang, P. Zhu, Q. Hu and D. Zhang, “A Linear Subspace Learning Approach via Sparse Coding,” in ICCV 2011.

网址：http://www4.comp.polyu.edu.hk/~cslzhang/   做稀疏表示做的非常棒，很多发表的paper，都附有code，这魄力，不服不行哈~

 

线性子空间学习（Linear subspace learning,LSL）,是通过线性投影，实现高维特征空间到低维空间的映射~

原有方法的缺点：大多的线性子空间学习，是直接从原始训练样本中统计学习子空间~ 但是在计算机视觉中，不同组件贡献也不同~~

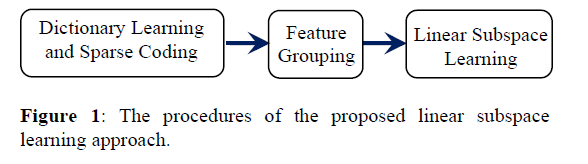
现提出：利用稀疏表示和特征分组----->子空间学习~

            首先从训练数据集中学习字典，以便用于稀疏的表示样本~

            字典中的图像组件，分了两类，利于分辨和不利于分辨的部分 （More / Less discriminant part；MDP/LDP）~

            无监督准则/有监督准则---->子空间学习。其中MDP保留，LDP抑制~

 

线性子空间学习方法，包括PCA、Eigenface、Fisher 线性判别式分析、基于LPP（locality preserving projection）流形学习、局部判别式嵌入（local discriminant embedding LDE）、图嵌入(graph embedding)。

根据是否利用训练样本的类别信息，可分为无监督的方法（PCA、LPP）和有监督的方法（FLDA、regularized LDA、LDE）。

线性子空间学习的方法，是通过一种确定的判别函数，学习理想的子空间或者投影方式~  

例如：PCA是寻找一种不相关（即是正交的）的最佳子空间。FLDA是通过最大化(类间方差/类内方差)比率，学习最佳子空间~

高维数据一般处于低维流形上，所以LSL(例如LPP)可以通过保留原始高位数据的几何图，学习子空间~

线性子空间学习中样本方差矩阵计算的问题~  不同组件有着不同的贡献~ 例如：噪声应有较小的贡献~   因此把图像分解为两类不同的组件，一类贡献比较大，一类贡献比较小~

 

稀疏表示（用于压缩、字典学习、影像组件分析）

首先从样本集中基于patch的思想，学习一个字典D，有k个元素/组件。 然后把这k个组件分为两类（MDP和LDP）。然后确定投影矩阵，投影之，进行分类~

本文方法的框架图：

一、字典学习和稀疏编码~

数据集有m个样本x~  每个样本都分为两个部分，MDP和LDP。

 

如果有一个测试样本y，则直接利用P进行投影，计算Py和PX的距离，利用NN进行分类之~

 

利用稀疏表示学习字典D。因为原始图像维数比较高，很难直接学习一个冗余字典。所以基于patch的思想进行学习之~

将每个训练样本分为q个重叠patch，最终由h=m*q的patch，其中m是样本数。

 

 

二、无监督子空间学习

在经过稀疏编码之后，每个图像被分解为k个特征图像。

 

 

三、有监督子空间学习