学习笔记【机器学习重点与实战】——3 决策树
学习笔记【机器学习重点与实战】——3 决策树
1.决策树
决策树（decision tree）是一种常见的机器学习方法，是一种基本的分类和回归方法。决策树模型呈树形结构，如下图所示，对鸢尾花数据采用决策树学习得到的3层决策树。
定义5.1（决策树） 分类决策树模型是一种描述对实例进行分类的树形结构，决策树由节点（node）和有向边（directededge）组成。结点有两种类型：内部结点（internal node）和叶结点（leafnode）。内部结点表示一个特征或属性，叶结点表示一个类。
用决策树分类，从根结点开始，对实例的某一特征进行测试，根据测试结果，将实例分配到其子结点：这时，每一个子结点对应着该特征的一个取值。如此递归地对实例进行测试并分配，直至达到叶结点。最后将实例分到叶结点的类中。
——《统计学习方法》 P55 P 55
优点：计算复杂度不高，输出结果易于理解，对中间值的缺失不敏感，可以处理不相关特征数据。
缺点：可能会产生过度匹配问题。
适用数据类型：数值型和标称型。——《机器学习实战》 P33 P 33
决策树的学习通常包括三个步骤：1.特征选择，2.树的生成，3.树的剪枝。
1.1特征选择
特征选择目的在于选取对训练数据能够分类的特征。特征选择的准则主要有信息增益、信息增益比、基尼指数，这三个准则也分别对应了决策树的三个代表算法： ID3[Quinlan,1979,1986] I D 3 [ Q u i n l a n , 1979 , 1986 ] 、 C4.5[Quinla，1993] C 4.5 [ Q u i n l a ， 1993 ] 和 CART[Breimanetal.,1984] C A R T [ B r e i m a n e t a l . , 1984 ] 。
1.1.1信息增益
设样本集合为D，特征A的信息增益 g(D,A) g ( D , A ) 为：
g(D,A)=H(D)−H(D|A) g ( D , A ) = H ( D ) − H ( D | A )
H(D)=−∑k=1K|Ck||D|log2|Ck||D| H ( D ) = − ∑ k = 1 K | C k | | D | l o g 2 | C k | | D |
H(D|A)=∑i=1n|Di||D|H(Di)=−∑i=1n|Di||D|(∑k=1K|Dik||Di|log2|Dik||Di|) H ( D | A ) = ∑ i = 1 n | D i | | D | H ( D i ) = − ∑ i = 1 n | D i | | D | ( ∑ k = 1 K | D i k | | D i | l o g 2 | D i k | | D i | )
其中， H(D) H ( D ) 是样本集D的熵， H(Di) H ( D i ) 是数据集 Di D i 的熵， H(D|A) H ( D | A ) 是样本集D对特征A的条件熵， Di D i 是D中特征取第i个值的样本子集， Ck C k 是D中属于第k类的样本子集。n是特征A取值的个数，K是类的个数。
1.1.2信息增益比（增益率）
信息增益对可取值数目较多的属性有所偏好，为减少这种偏好带来的不利影响，C4.5算法则使用“信息增益比（增益率）”来选择最优划分属性。设样本集合为D，特征A的信息增益比 gR(D,A) g R ( D , A ) 为：
gR(D,A)=g(D,A)HA(D) g R ( D , A ) = g ( D , A ) H A ( D )
HA(D)=−∑i=1n|Di||D|log2|Di||D| H A ( D ) = − ∑ i = 1 n | D i | | D | l o g 2 | D i | | D |
g(D,A) g ( D , A ) 为特征A的信息增益， HA(D) H A ( D ) 为特征A在数据集D的信息熵，n是特征A取值的个数。
需注意的是，增益率准则对可取值数目较少的属性有所偏好，因此， C4.5[Quinla，1993] C 4.5 [ Q u i n l a ， 1993 ] 算法并不是直接选择增益率最大的候选划分属性，而是使用了一个启发式，先从候选划分属性中找出信息增益高于平均水平的属性，再从中选择增益率最高的。
——《机器学习 - 周志华》 P78 P 78
1.1.3基尼指数
样本集 D 的纯度可用基尼值来度量：
Gini(D)=∑k=1Kpk(1−pk)=1−∑k=1Kp2k=1−∑k=1K(|Ck||D|)2 G i n i ( D ) = ∑ k = 1 K p k ( 1 − p k ) = 1 − ∑ k = 1 K p k 2 = 1 − ∑ k = 1 K ( | C k | | D | ) 2
其中， Ck C k 是D中属于第k类的样本子集，K是类的个数。
直观来说， Gini(D) G i n i ( D ) 反映了从数据集 D 中随机抽取两个样本，其类别标记不一致的概率。因此， Gini(D) G i n i ( D ) 越小，则数据集 D 的纯度越高。
若样本集 D 根据特征 A 被分割成 n 个部分，则在特征 A 条件下，D 的基尼指数为：
Gini(D,A)=∑n=1n|Di||D|Gini(Di) G i n i ( D , A ) = ∑ n = 1 n | D i | | D | G i n i ( D i )
1.2树的生成
通常使用信息增益最大、信息增益比最大或基尼指数最小作为特征选择的准则，即降低样本集 D 的不确定性，决策树的生成往往通过计算信息增益或其他指标，从根结点开始，递归地产生决策树，这相当于用信息增益或其他准则不断地选取局部最优的特征，或将训练集分割为能够基本正确分类的子集。
决策树基本学习算法如下：
输入：训练集 D = {(X1,Y1) , (X2,Y2)，...,(Xm,Ym)};
属性集 A={α1,a2,...,ad}
过程：函数TreeGenerate(D,A)
1: 生成结点 node;
2: if D 中样本全属于同一类别 C then
3: 将 node 标记为 C 类叶结点 return # 递归返回，情形 (1)
4: end if
5: if A=∅ OR D 中样本在 A 上取值相同 then
6: 将 node 标记为叶结点，其类别标记为 D 中样本数最多的类; return # 递归返回，情形 (2)
7: end if
8: 从 A 中选择最优划分属性a;
9: for a的每一个值 ai do
10: 为 node 生成一个分支;令 Dv 表示 D 中在 a 上取值为 av 的样本子集;
11: if Dv 为空 then
12: 将分支结点标记为叶结点，其类别标记为 D 中样本最多的类; return # 递归返回，情形 (3)
13: else
14: 以TeeGenerate(Dv,A \ {α})为分支结点 # 从 A 中去掉 α
15: end if
16: end for
输出：以 node 为根结点的一棵决策树 ——《机器学习-周志华》 P74 P 74
1.3树的剪枝
由于生成的决策树存在过拟合问题，需要对它进行剪枝，以简化学到的决策树。决策树的剪枝，往往从己生成的树上剪掉一些叶结点或叶结点以上的子树，并将其父结点或根结点作为新的叶结点，从而简化生成的决策树。
决策树剪枝的基本策略有”预剪枝” (prepruning)和”后剪枝 “(post-pruning) [Quinlan, 1993]。
预剪枝是指在决策树生成过程中，对每个结点在划分前先进行估计，若当前结点的划分不能带来决策树泛化性能提升，则停止划分并将当前结点标记为叶结点。
后剪枝则是先从训练集生成一棵完整的决策树，然后自底向上地对非叶结点进行考察，若将该结点对应的子树替换为叶结点能带来决策树泛化性能提升，则将该子树替换为叶结点。
——《机器学习-周志华》 P79 P 79
2.决策树常用算法实现
2.1 ID3（信息增益）
实现代码如下：
""" 计算给定数据集的经验熵（香农熵） Args: dataSet - 数据集 Returns: shannonEnt - 经验熵（香农熵） Author: dkjkls Blog: https://blog.csdn.net/dkjkls Modify: 2018/4/1 0:35 """
def calcShannonEnt(dataSet):
numEntries = len(dataSet) # 数据集行数
labelCounts = {} # 标签出现次数的字典
for featVec in dataSet: # 遍历数据集
currentLabel = featVec[-1] # 获取标签信息
if currentLabel not in labelCounts.keys(): # 若字典中未添加该标签，则添加进字典
labelCounts[currentLabel] = 0
labelCounts[currentLabel] += 1 # 对标签进行计数
shannonEnt = 0.0 # 初始化经验熵（香农熵）
for key in labelCounts: # 计算经验熵（香农熵）
prob = float(labelCounts[key])/numEntries # 该标签的概率
shannonEnt -= prob * log(prob,2) # 经验熵公式
return shannonEnt # 返回经验熵（香农熵）
""" 划分数据集 Args: dataSet - 待划分的数据集 axis - 划分数据集的特征 value - 需要返回的特征的值 Returns: retDataSet - 划分后的数据集 Author: dkjkls Blog: https://blog.csdn.net/dkjkls Modify: 2018/4/1 0:46 """
def splitDataSet(dataSet, axis, value):
retDataSet = [] # 初始化划分数据集
for featVec in dataSet: # 遍历数据集
if featVec[axis] == value: # 该条样本选取的特征为传入的特征值
reducedFeatVec = featVec[:axis] # 去掉axis特征
reducedFeatVec.extend(featVec[axis + 1:])
retDataSet.append(reducedFeatVec) # 添加符合条件的数据集
return retDataSet # 返回划分后的数据集
""" 选取最优的数据集划分方式 Args: dataSet - 数据集 Returns: bestFeature - 信息增益最大的特征的索引值 Author: dkjkls Blog: https://blog.csdn.net/dkjkls Modify: 2018/4/1 1:10 """
def chooseBestFeatureToSplit(dataSet):
numFeatures = len(dataSet[0]) - 1 # 特征数量
baseEntropy = calcShannonEnt(dataSet) # 样本集的信息熵
bestInfoGain = 0.0 # 最优的信息增益
bestFeature = -1 # 最优特征的索引
for i in range(numFeatures): # 遍历所有特征
featList = [example[i] for example in dataSet] # 获取第i个所有特征值
uniqueVals = set(featList) # 获取不重复的第i个特征值
newEntropy = 0.0 # 初始化经验熵
for value in uniqueVals: # 遍历第i个特征值的取值
subDataSet = splitDataSet(dataSet, i, value) # 划分子集
prob = len(subDataSet)/float(len(dataSet)) # 子集概率
newEntropy += prob * calcShannonEnt(subDataSet) # 条件熵
infoGain = baseEntropy - newEntropy # 信息增益
if (infoGain > bestInfoGain): # 找出最大的信息增益
bestInfoGain = infoGain # 更新信息增益最大值
bestFeature = i # 记录信息增益最大的特征的索引值
return bestFeature # 返回信息增益最大的特征的索引值
""" 统计类标签中出现次数最多的标签 Args: classList - 类标签列表 Returns: classList - 类标签 Author: dkjkls Blog: https://blog.csdn.net/dkjkls Modify: 2018/4/1 8:45 """
def majorityCnt(classList):
classCount={} # 类标签出现次数的字典
for vote in classList: # 遍历统计各类标签出现的次数
if vote not in classCount.keys(): classCount[vote] = 0
classCount[vote] += 1
sortedClassCount = sorted(classCount.iteritems(), key=operator.itemgetter(1), reverse=True)
return sortedClassCount[0][0] # 返回出现次数最多的标签
""" 创建决策树 Args: dataSet - 数据集 labels - 类标签 Returns: myTree - 决策树 Author: dkjkls Blog: https://blog.csdn.net/dkjkls Modify: 2018/4/1 8:52 """
def createTree(dataSet,labels):
classList = [example[-1] for example in dataSet] # 取分类标签
if classList.count(classList[0]) == len(classList): # 若类标签完全相同，直接返回该类标签
return classList[0]
if len(dataSet[0]) == 1: # 遍历完所有特征时返回出现次数最多的类别
return majorityCnt(classList)
bestFeat = chooseBestFeatureToSplit(dataSet) # 选取最优的数据集划分方式
bestFeatLabel = labels[bestFeat] # 最优特征的类标签
myTree = {bestFeatLabel:{}} # 初始化决策树字典
del(labels[bestFeat]) # 删除已经使用过的类标签
featValues = [example[bestFeat] for example in dataSet] # 选取集合中所有最优特征的属性值
uniqueVals = set(featValues) # 得到不重复的属性值
for value in uniqueVals: #遍历特征，创建决策树
subLabels = labels[:] # 复制所有标签
# 递归调用创建决策树函数
myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet, bestFeat, value),subLabels)
return myTree # 返回创建好的决策树sklearn中的决策树使用的是CART，为二叉树，稍稍有区别的是它对CART的计算性能进行了优化。可以设置sklearn.tree.DecisionTreeClassifier中criterion参数为”entropy”，也就是信息增益，但ID3为多叉树，只能近似看做是ID3。
sklearn中ID3类似实现代码如下：
from sklearn.tree import DecisionTreeClassifier
model = DecisionTreeClassifier(criterion='entropy')
model.fit(x_train, y_train) # 建立决策树
y_test_hat = model.predict(x_test) # 测试数据2.2 C4.5（信息增益比）
C4.5与ID3的仅在特征选择上有区别，C4.5的实现只需在ID3实现的基础上替换特征选择的准则，从信息增益替换为信息增益比即可。具体为将chooseBestFeatureToSplit(dataSet)函数替换为chooseBestFeatureToSplitGainRatio(dataSet)，具体代码如下：
""" 选取最优的数据集划分方式（增益率） Args: dataSet - 数据集 Returns: bestFeature - 增益率最大的特征的索引值 Author: dkjkls Blog: https://blog.csdn.net/dkjkls Modify: 2018/4/1 1:10 """
def chooseBestFeatureToSplitGainRatio(dataSet):
numFeatures = len(dataSet[0]) - 1 # 特征数量
baseEntropy = calcShannonEnt(dataSet) # 样本集的信息熵
bestInfoGain = 0.0 # 最优的信息增益率
bestFeature = -1 # 最优特征的索引
for i in range(numFeatures): # 遍历所有特征
featList = [example[i] for example in dataSet] # 获取第i个所有特征值
uniqueVals = set(featList) # 获取不重复的第i个特征值
newEntropy = 0.0 # 初始化条件熵
splitInfo = 0.0 # 初始化数据集的经验熵
for value in uniqueVals: # 遍历第i个特征值的取值
subDataSet = splitDataSet(dataSet, i, value) # 划分子集
prob = len(subDataSet)/float(len(dataSet)) # 子集概率
newEntropy += prob * calcShannonEnt(subDataSet) # 条件熵
splitInfo -= prob * log(prob,2) # 计算数据集的经验熵
infoGain = (baseEntropy - newEntropy)/splitInfo # 信息增益率
if (infoGain > bestInfoGain): # 找出最大的信息增益率
bestInfoGain = infoGain # 更新信息增益率最大值
bestFeature = i # 记录信息增益率最大的特征的索引值
return bestFeature # 返回信息增益率最大的特征的索引值2.3 CART（基尼指数）
2.3.1 回归树的构建
实现代码如下：
""" 数据集合切分 Args: dataSet - 数据集合 feature - 待切分的特征 value - 该特征的值 Returns: mat0 - 切分后的数据集合0，大于value mat1 - 切分后的数据集合1，小于等于value Author: dkjkls Blog: https://blog.csdn.net/dkjkls Modify: 2018/4/1 10:15 """
def binSplitDataSet(dataSet, feature, value):
mat0 = dataSet[np.nonzero(dataSet[:,feature] > value)[0],:][0]
mat1 = dataSet[np.nonzero(dataSet[:,feature] <= value)[0],:][0]
return mat0,mat1
""" 生成叶节点 Args: dataSet - 数据集 Returns: mean - 目标变量的均值 Author: dkjkls Blog: https://blog.csdn.net/dkjkls Modify: 2018/4/1 10:26 """
def regLeaf(dataSet):
return np.mean(dataSet[:,-1])
""" 误差估计函数 Args: dataSet - 数据集 Returns: var - 目标变量的总方差 Author: dkjkls Blog: https://blog.csdn.net/dkjkls Modify: 2018/4/1 10:28 """
def regErr(dataSet):
return np.var(dataSet[:,-1]) * np.shape(dataSet)[0]
""" 选择数据集的最佳二元切分方式 Args: dataSet - 数据集合 leafType - 生成叶结点 regErr - 误差估计函数 ops - 用户定义的参数元组 Returns: bestIndex - 最佳切分特征 bestValue - 最佳特征值 Author: dkjkls Blog: https://blog.csdn.net/dkjkls Modify: 2018/4/1 10:30 """
def chooseBestSplit(dataSet, leafType=regLeaf, errType=regErr, ops=(1,4)):
tolS = ops[0] # 允许的误差下降值
tolN = ops[1] # 切分的最少样本数
if len(set(dataSet[:,-1].T.tolist()[0])) == 1: # 如果当前所有特征值相等则退出
return None, leafType(dataSet)
m, n = np.shape(dataSet) # 集合的行m和列n值
S = errType(dataSet) # 初始化最后一个特征为最佳切分特征，计算误差估计
bestS = np.inf; bestIndex = 0; bestValue = 0 # 初始化最佳值
for featIndex in range(n-1): # 遍历特征列
for splitVal in set(dataSet[:,featIndex]): # 遍历特征列的所有特征值
mat0, mat1 = binSplitDataSet(dataSet, featIndex, splitVal) # 切分集合
if (np.shape(mat0)[0] < tolN) or (np.shape(mat1)[0] < tolN): continue # 如果数据少于切分的最少样本数，则继续遍历
newS = errType(mat0) + errType(mat1) # 计算切分后的误差估计值
if newS < bestS: # 如果误差更小，则更新最优特征索引值和特征值
bestIndex = featIndex
bestValue = splitVal
bestS = newS
if (S - bestS) < tolS: # 如果误差减小小于允许的误差下降值则退出
return None, leafType(dataSet)
mat0, mat1 = binSplitDataSet(dataSet, bestIndex, bestValue) # 根据最优特征索引值和特征值切分数据集
if (np.shape(mat0)[0] < tolN) or (np.shape(mat1)[0] < tolN): # 如果数据少于切分的最少样本数，则退出
return None, leafType(dataSet)
return bestIndex,bestValue # 返回最佳切分特征和特征值
""" 构建树 Args: dataSet - 数据集合 leafType - 生成叶结点 regErr - 误差估计函数 ops - 用户定义的参数元组 Returns: retTree - 构建的回归树 Author: dkjkls Blog: https://blog.csdn.net/dkjkls Modify: 2018/4/1 13:49 """
def createTree(dataSet, leafType=regLeaf, errType=regErr, ops=(1,4)):
feat, val = chooseBestSplit(dataSet, leafType, errType, ops) # 选择数据集的最佳二元切分方式，得到最佳切分特征和特征值
if feat == None: return val # 如果没有最佳切分特征，则返回特征值
retTree = {} # 初始化决策树
retTree['spInd'] = feat
retTree['spVal'] = val
lSet, rSet = binSplitDataSet(dataSet, feat, val) # 数据集切分为左右数据集
retTree['left'] = createTree(lSet, leafType, errType, ops) # 创建左子树
retTree['right'] = createTree(rSet, leafType, errType, ops) # 创建右子树
return retTree # 返回决策树2.3.2 回归树的后剪枝
实现代码如下：
""" 判断输入变量是否为一个树 Args: obj - 测试对象 Returns: Boolean - 是否是一棵树 Author: dkjkls Blog: https://blog.csdn.net/dkjkls Modify: 2018/4/1 14:05 """
def isTree(obj):
return (type(obj).__name__=='dict')
""" 对树进行塌陷处理(即返回树平均值) Args: tree - 输入的树 Returns: 树的平均值 Author: dkjkls Blog: https://blog.csdn.net/dkjkls Modify: 2018/4/1 14:07 """
def getMean(tree):
if isTree(tree['right']): tree['right'] = getMean(tree['right'])
if isTree(tree['left']): tree['left'] = getMean(tree['left'])
return (tree['left']+tree['right'])/2.0
""" 树的后剪枝 Args: tree - 树 test - 测试集 Returns: 剪枝后的树 Author: dkjkls Blog: https://blog.csdn.net/dkjkls Modify: 2018/4/1 14:08 """
def prune(tree, testData):
if np.shape(testData)[0] == 0: return getMean(tree) # 如果测试集为空，则塌陷处理
if (isTree(tree['right']) or isTree(tree['left'])): # 如果有左子树或右子树则切分数据集
lSet, rSet = binSplitDataSet(testData, tree['spInd'], tree['spVal'])
if isTree(tree['left']): tree['left'] = prune(tree['left'], lSet) # 对左子树进行剪枝
if isTree(tree['right']): tree['right'] = prune(tree['right'], rSet) # 对右子树进行剪枝
if not isTree(tree['left']) and not isTree(tree['right']): # 当前节点的左右节点均为叶节点
lSet, rSet = binSplitDataSet(testData, tree['spInd'], tree['spVal'])# 数据集合切分
# 合并前的误差
errorNoMerge = sum(np.power(lSet[:, -1] - tree['left'], 2)) + sum(np.power(rSet[:, -1] - tree['right'], 2))
treeMean = (tree['left']+tree['right'])/2.0 # 合并后的均值
errorMerge = sum(np.power(testData[:, -1] - treeMean, 2)) # 合并后的误差
if errorMerge < errorNoMerge: # 如果合并后的误差小于合并前的误差,则合并
print("merging")
return treeMean # 返回剪枝后叶节点的均值
else: return tree # 返回剪枝树
else: return tree # 返回剪枝树3.实战
3.1 sklearn决策树分类
3.1.1 鸢尾花数据集决策树分类
实现代码如下：
import pandas as pd
from sklearn import tree
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.preprocessing import LabelEncoder
import pydotplus
if __name__ == "__main__":
iris_feature_E = 'sepal length', 'sepal width', 'petal length', 'petal width'
iris_feature = '花萼长度', '花萼宽度', '花瓣长度', '花瓣宽度'
iris_class = 'Iris-setosa', 'Iris-versicolor', 'Iris-virginica'
path = 'iris.data' # 数据文件路径
data = pd.read_csv(path, header=None) # 读取数据
x = data[list(range(4))] # 取特征值
y = LabelEncoder().fit_transform(data[4]) # 使用sklearn的LabelEncoder取标签值 或 y = pd.Categorical(data[4]).codes
# 拆分数据为训练集（70%）和测试集（30%）
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=1)
# 使用sklearn的DecisionTreeClassifier，基尼系数作为评价函数
model = DecisionTreeClassifier(criterion='gini')
model.fit(x_train, y_train) # 建立决策树
y_test_hat = model.predict(x_test) # 测试数据
print('训练集准确率:', accuracy_score(y_test, y_test_hat))
# 输出决策树图形
with open('iris.dot', 'w') as f:
tree.export_graphviz(model, out_file=f)
dot_data = tree.export_graphviz(model, out_file=None, feature_names=iris_feature_E[0:2], class_names=iris_class, filled=True, rounded=True, special_characters=True)
graph = pydotplus.graph_from_dot_data(dot_data)
graph.write_pdf('iris.pdf')
f = open('iris.png', 'wb')
f.write(graph.create_png())
f.close()输出结果如下：
训练集准确率: 0.955555555556输出的决策树图形如下：
从根结点看起，若petal width ≤ 0.8，则为其左侧的叶节点，即为Iris-setosa；若petal width > 0.8，则为其右子树。
3.1.2 sklearn决策树深度与过拟合现象
训练数据仍为鸢尾花数据集，为了展示决策树随深度增加而产生的过拟合现象，仅使用前两列特征，即“花萼长度”和“花萼宽度”。
实现代码如下：
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib as mpl
from sklearn import tree
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score
from sklearn.preprocessing import LabelEncoder
if __name__ == "__main__":
mpl.rcParams['font.sans-serif'] = ['simHei']
mpl.rcParams['axes.unicode_minus'] = False
iris_feature_E = 'sepal length', 'sepal width', 'petal length', 'petal width'
iris_feature = '花萼长度', '花萼宽度', '花瓣长度', '花瓣宽度'
iris_class = 'Iris-setosa', 'Iris-versicolor', 'Iris-virginica'
path = 'iris.data' # 数据文件路径
data = pd.read_csv(path, header=None) # 读取数据
x = data[list(range(4))] # 取特征值
y = LabelEncoder().fit_transform(data[4]) # 使用sklearn的LabelEncoder取标签值 或 y = pd.Categorical(data[4]).codes
x = x.iloc[:, :2] # 为了可视化，仅使用前两列特征 或 x = x[[0,1]]
# 拆分数据为训练集（70%）和测试集（30%）
x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=1)
# 过拟合：错误率
depth = np.arange(1, 15)
err_list = []
# 遍历决策树深度
for d in depth:
# 使用sklearn的DecisionTreeClassifier，基尼系数作为评价函数
clf = DecisionTreeClassifier(criterion='gini', max_depth=d)
clf.fit(x_train, y_train)
y_test_hat = clf.predict(x_test) # 测试数据
err = 1 - accuracy_score(y_test, y_test_hat) # 计算错误率
err_list.append(err)
print(d, ' 错误率: %.2f%%' % (100 * err))
plt.figure(facecolor='w')
plt.plot(depth, err_list, 'ro-', markeredgecolor='k', lw=2)
plt.xlabel('决策树深度', fontsize=13)
plt.ylabel('错误率', fontsize=13)
plt.title('决策树深度与过拟合', fontsize=15)
plt.grid(b=True, ls=':', color='#606060')
plt.show()输出结果如下：
1 错误率: 44.44%
2 错误率: 24.44%
3 错误率: 24.44%
4 错误率: 24.44%
5 错误率: 24.44%
6 错误率: 33.33%
7 错误率: 35.56%
8 错误率: 35.56%
9 错误率: 37.78%
10 错误率: 37.78%
11 错误率: 40.00%
12 错误率: 37.78%
13 错误率: 37.78%
14 错误率: 40.00%输出的决策树深度与错误率关系图如下：
由上图可知，决策树深度为2/3/4/5时，错误率最低；深度为1时，为欠拟合；深度超过5时逐渐过拟合。
3.2 sklearn决策树回归
实现代码如下：
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from sklearn.tree import DecisionTreeRegressor
if __name__ == "__main__":
# 生成样本点
N = 100
x = np.random.rand(N) * 6 - 3 # [-3,3)
x.sort()
y = np.sin(x) + np.random.randn(N) * 0.05
x = x.reshape(-1, 1)
# 比较决策树的深度影响
depth = [2, 4, 6, 8, 10]
clr = 'rgbmy'
dtr = DecisionTreeRegressor(criterion='mse') # 决策树回归
mpl.rcParams['font.sans-serif'] = ['SimHei']
mpl.rcParams['axes.unicode_minus'] = False
plt.figure(facecolor='w')
plt.plot(x, y, 'ro', ms=5, mec='k', label='实际值')
x_test = np.linspace(-3, 3, 50).reshape(-1, 1)
for d, c in zip(depth, clr):
dtr.set_params(max_depth=d) # 设置决策树深度
dtr.fit(x, y) # 生成决策树
y_hat = dtr.predict(x_test) # 预测测试集
plt.plot(x_test, y_hat, '-', color=c, linewidth=2, markeredgecolor='k', label='Depth=%d' % d)
plt.legend(loc='upper left', fontsize=12)
plt.xlabel('X')
plt.ylabel('Y')
plt.grid(b=True, ls=':', color='#606060')
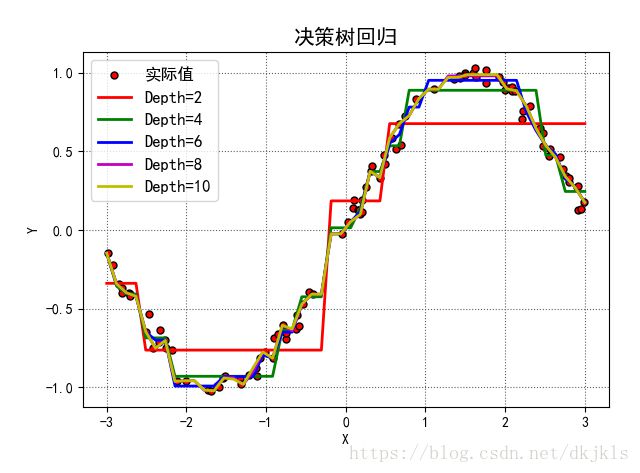
plt.title('决策树回归', fontsize=15)
plt.tight_layout(2)
plt.show()输出结果如下：
4.参考
- 机器学习升级版视频 - 邹博
- 《机器学习实战》第3章 决策树
- 《机器学习实战》第9章 树回归
- 《机器学习 - 周志华》第4章 决策树
- 《统计学习方法》第5章 决策树
===============文档信息================
学习笔记由博主整理编辑，供非商用学习交流用
如本文涉及侵权，请随时留言博主，必妥善处置
版权声明：非商用自由转载-保持署名-注明出处
署名(BY) ：dkjkls（dkj卡洛斯）
文章出处：http://blog.csdn.net/dkjkls