吃豆子过桥

flyfish 2015-10-15

一个人要过一座 80 米的桥，每走一米需要吃一颗豆子，他最多可以装 60 颗豆子，问最少需要吃多少颗豆子才能走完桥？

设 桥长：长度 L
最多装多少颗豆子 容量 C

分析
情况1：L <= C 一次就可以

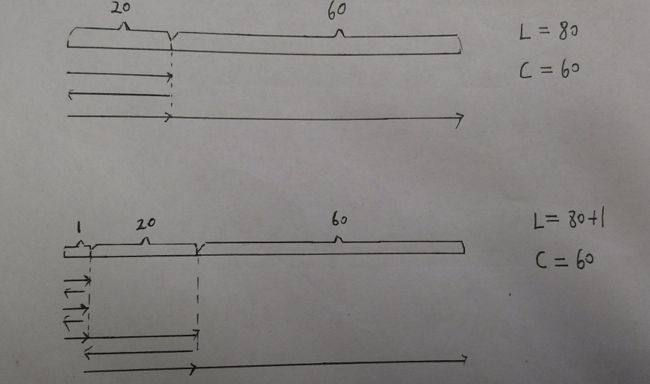
情况2：原长度是L，从L=C开始 ，在原来基础上长度每次加1，加到L=80

原题L=80,C=60，

L=L+1 消耗 1*2+1+C
L=L+2 消耗 2*2+2+C=(1*2+1+C)+1*2+1
L=L+3 消耗 3*2+3+C=(2*2+2+C)+1*2+1
L=L+4 消耗 4*2+4+C=(3*2+3+C)+1*2+1
. .
. .
. .
L=L+19 消耗 19*2+19+C=(18*2+18+C)+1*2+1
L=L+20 消耗 20*2+20+C=(19*2+19+C)+1*2+1

结果
40+20+C
=40+20+60
=120 所以要消耗120

继续
至此规律发送变化 1*2+1 变成了 (1*4+1)
因为在21的位置需要1个来回，在1的位置需要2个来回

L=L+21 消耗 (1*4+1)+60+C= 20*2+20+ C+(1*4+1)
L=L+22 消耗 (2*4+2)+60+C=(1*4+1)+60 + C+(1*4+1)
L=L+23 消耗 (3*4+3)+60+C=(2*4+2)+60 + C+(1*4+1)
L=L+24 消耗 (4*4+4)+60+C=(3*4+3)+60 + C+(1*4+1)
L=L+25 消耗 (5*4+5)+60+C=(4*4+4)+60 + C+(1*4+1)

将设R为往返次数
f(L,C)=f(L-1,C) + 2R + 1
求R

最后1次到达1的时候剩余（C-1）
在此之前到达此处的1,因为要回去运所以 剩余（C-2）,
R是往返次数，不包括最后一次

f(L-1,C) <= （C-1）+ (C-2)*R
R>=（ f(L-1,C) - (C-1) ）/ (C-2)

int CalcLoop(int L, int C)
{
    int ret=C;
    for(int i=C; i2) / (C-2) * 2 + 1);

    return ret;
}

递归思考
例如如果要求L=80,C=60的损耗，那么先要知道L=79,C=60
如果要求L=79,C=60的损耗，那么先要知道L=78,C=60
递归停止到L=60,C=60

相当于
如果求f(L,C)的值，那么先求f(L-1,C)
如果求f(L-1,C)的值，那么先求f(L-2,C)
递归停止到L=C

int CalcRecursion(int L, int C) 
{
    if(L <= C)
        return L;
    int ret = CalcRecursion(L-1,C);  
    return ret + ceil((double)(ret-(C-1))/(C-2)) * 2 + 1;
}

图

火车运煤问题

你是山西的一个煤老板，你在矿区开采了有3000吨煤需要运送到市场上去卖，从你的矿区到市场有1000公里，你手里有一列烧煤的火车，这个火车最多只能装1000吨煤，且其能耗比较大——每一公里需要耗一吨煤。请问，作为一个懂编程的煤老板的你，你会怎么运送才能运最多的煤到集市？

通过上述推理火车运煤的问题很好解决

L=1000
C=1000
问题发生变化
吃豆是需要吃多少颗豆子才能走完桥
运煤是运最多的煤
设置往返点
最后一个往返点 1000/3=333。
第一个往返点是1000/5=200 .
结果是533。

如果是上述的那个豆子
豆子问题是60/3=20
60/5=12
在12之内的规律都是1*4+1