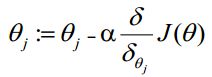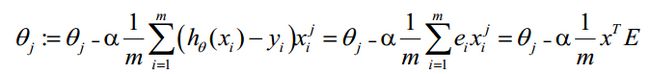机器学习实战之 Logistic算法
Logistic 回归
1.基本步骤
Logistic回归:实际上属于判别分析,因拥有很差的判别效率而不常使用。
逻辑回归的一般过程
1) 收集数据:采用任意方法收集数据。
2) 准备数据:由于需要进行距离计算,因此要求数据类型为数值型。另外,结构化数据格式则最佳。
3) 分析数据:采用任意方法对数据进行分析。
4) 训练算法:大部分时间将用于训练,训练的目的是为了找到最佳分类回归系数。
5) 测试算法:一旦训练步骤完成,分类将会很快。
6) 使用算法:首先,我们需要输入一些数据,并将其转换成对应的结构化数值;接着,基于训练好的回归系数就可以对这些数值进行简单的回归计算,判定它们属于哪个类型;在这之后,我们就可以在输出的类别上作一些其他的分析工作。
优点:
1. 计算复杂度低,易于实施
2. 表示形式易于翻译
缺点:
易于欠拟合,
2.原理
2.1常规步骤
Regression问题的常规步骤为:
- 寻找h函数(即hypothesis);
- 构造J函数(log损失函数);
- 想办法使得J函数最小并求得回归参数(θ)
2.2构造预测函数h
Logistic回归虽然名字里带“回归”,但是它实际上是一种分类方法,主要用于两分类问题(即输出只有两种,分别代表两个类别),所以利用了Logistic函数(或称为Sigmoid函数),函数形式为:
Sigmoid 函数在有个很漂亮的“S”形,如下图所示(引自维基百科):
下面左图是一个线性的决策边界,右图是非线性的决策边界。
对于线性边界的情况,边界形式如下:
构造预测函数为:
函数的值有特殊的含义,它表示结果取1的概率,因此对于输入x分类结果为类别1和类别0的概率分别为:
2.3构造损失函数J
损失函数使用log损失函数。Cost函数和J函数如下,它们是基于最大似然估计推导得到的。
下面详细说明推导的过程:
(1)式综合起来可以写成:
取似然函数为:
对数似然函数为:
最大似然估计就是求使![]() 取最大值时的θ,其实这里可以使用梯度上升法求解,求得的θ就是要求的最佳参数。但是,在Andrew Ng的课程中将
取最大值时的θ,其实这里可以使用梯度上升法求解,求得的θ就是要求的最佳参数。但是,在Andrew Ng的课程中将![]() 取为下式,即:
取为下式,即:
因为乘了一个负的系数-1/m,所以取![]() 最小值时的θ为要求的最佳参数。
最小值时的θ为要求的最佳参数。
梯度下降法求的最小值
θ更新过程:
θ更新过程可以写成:
向量化Vectorization
Vectorization是使用矩阵计算来代替for循环,以简化计算过程,提高效率。
如上式,Σ(...)是一个求和的过程,显然需要一个for语句循环m次,所以根本没有完全的实现vectorization。
下面介绍向量化的过程:
约定训练数据的矩阵形式如下,x的每一行为一条训练样本,而每一列为不同的特称取值:
g(A)的参数A为一列向量,所以实现g函数时要支持列向量作为参数,并返回列向量。由上式可知![]() 可由
可由![]() 一次计算求得。
一次计算求得。
θ更新过程可以改为:
综上所述,Vectorization后θ更新的步骤如下:
(2)求![]() ;
;
3.Python 求解Logistic 回归
训练样本当中有100个样本,每个样本有两个特征:X1和X2.
3.1 用梯度上升法寻找最优参数
def getData():
dataMat = []
labels=[]
fr = open('data/Ch05/testSet.txt')
for line in fr.readlines():
linearr=line.split()
dataMat.append([1.0,float(linearr[0]),float(linearr[1])])
labels.append(float(linearr[2]))
return dataMat,labels
def sigmod(intX):
result = []
for x in intX:
result.append( 1.0/(1+exp(-1.0*x)))
return result
def gradAscent(dataMatIn, classLabels):
dataMatrix = mat(dataMatIn) #convert to NumPy matrix
labelMat = mat(classLabels).transpose() #convert to NumPy matrix
m,n = shape(dataMatrix)
alpha = 0.001
maxCycles = 500
weights = ones((n,1))
for k in range(maxCycles): #heavy on matrix operations
h = sigmoid(dataMatrix*weights) #matrix mult
error = (labelMat - h) #vector subtraction
weights = weights + alpha * dataMatrix.transpose()* error #matrix mult
return weights
def plotBestFit(weights):
import matplotlib.pyplot as plt
dataMat,labels=getData()
dataArr = array(dataMat)
n = shape(dataMat)[0]
xcord1=[];ycord1=[]
xcord2=[];ycord2=[]
for i in range(n):
if int(labels[i])==1:
xcord1.append(dataArr[i,1]);
ycord1.append(dataArr[i,2])
else:
xcord2.append(dataArr[i,1])
ycord2.append(dataArr[i,2])
fig=plt.figure()
ax = fig.add_subplot(111)
plt.scatter(xcord1,ycord1,s=30,c='red',marker='s')
plt.scatter(xcord2,ycord2,s=30,c='green')
x=arange(-3.0,3.0,0.1)
weights=array(weights)
y=(-1*weights[0]-weights[1]*x)/weights[2]
y=array(y)
plt.plot(x,y)
plt.xlabel('X1')
plt.ylabel('X2')
plt.show()
3.2 用随机梯度上升法寻找最优参数
def getData():
dataMat = []
labels=[]
fr = open('data/Ch05/testSet.txt')
for line in fr.readlines():
linearr=line.split()
dataMat.append([1.0,float(linearr[0]),float(linearr[1])])
labels.append(float(linearr[2]))
return dataMat,labels
def sigmod(intX):
result=1.0/(1+exp(-1.0*intX))
return result
def gradAscent(dataMatIn, classLabels):
dataMatrix = mat(dataMatIn) #convert to NumPy matrix
labelMat = mat(classLabels).transpose() #convert to NumPy matrix
m,n = shape(dataMatrix)
alpha = 0.001
maxCycles = 500
weights = ones((n,1))
for k in range(maxCycles): #heavy on matrix operations
h = sigmoid(dataMatrix*weights) #matrix mult
error = (labelMat - h) #vector subtraction
weights = weights + alpha * dataMatrix.transpose()* error #matrix mult
return weights
def stocGradAscent0(dataMatrix, classLabels):
m,n = shape(dataMatrix)
alpha = 0.01
weights = ones(n) #initialize to all ones
for i in range(m):
h = sigmoid(sum(dataMatrix[i]*weights))
error = classLabels[i] - h
weights = weights + alpha * error * dataMatrix[i]
return weights
def plotBestFit(weights):
import matplotlib.pyplot as plt
dataMat,labels=getData()
dataArr = array(dataMat)
n = shape(dataMat)[0]
xcord1=[];ycord1=[]
xcord2=[];ycord2=[]
for i in range(n):
if int(labels[i])==1:
xcord1.append(dataArr[i,1]);
ycord1.append(dataArr[i,2])
else:
xcord2.append(dataArr[i,1])
ycord2.append(dataArr[i,2])
fig=plt.figure()
ax = fig.add_subplot(111)
plt.scatter(xcord1,ycord1,s=30,c='red',marker='s')
plt.scatter(xcord2,ycord2,s=30,c='green')
x=arange(-3.0,3.0,0.1)
weights=array(weights)
y=(-1*weights[0]-weights[1]*x)/weights[2]
y=array(y)
plt.plot(x,y)
plt.xlabel('X1')
plt.ylabel('X2')
plt.show()
3.3 用改进的随机梯度上升法寻找最优参数
由于随机训练样本比较少,所以用随机梯度上升法求解结果较差,可以多运行几次随机梯度上升法同样可以得到很好的结果。
def getData():
dataMat = []
labels=[]
fr = open('data/Ch05/testSet.txt')
for line in fr.readlines():
linearr=line.split()
dataMat.append([1.0,float(linearr[0]),float(linearr[1])])
labels.append(float(linearr[2]))
return dataMat,labels
def sigmod(intX):
if(intX>100):return 1.0
if(intX<-100):return 0.0
result = 1.0/(1+exp(-1.0*intX))
return result
def plotBestFit(weights):
import matplotlib.pyplot as plt
dataMat,labels=getData()
dataArr = array(dataMat)
n = shape(dataMat)[0]
xcord1=[];ycord1=[]
xcord2=[];ycord2=[]
for i in range(n):
if int(labels[i])==1:
xcord1.append(dataArr[i,1]);
ycord1.append(dataArr[i,2])
else:
xcord2.append(dataArr[i,1])
ycord2.append(dataArr[i,2])
fig=plt.figure()
ax = fig.add_subplot(111)
plt.scatter(xcord1,ycord1,s=30,c='red',marker='s')
plt.scatter(xcord2,ycord2,s=30,c='green')
x=arange(-3.0,3.0,0.1)
weights=array(weights)
y=(-1*weights[0]-weights[1]*x)/weights[2]
y=array(y)
plt.plot(x,y)
plt.xlabel('X1')
plt.ylabel('X2')
plt.show()
def stocGradAscent(dataMatrix,classLabels,numIter=150):
m,n=shape(dataMatrix)
weights=ones(n)
dataIndex =list(range(m))
for j in range(numIter):
for i in range(m):
alpha = 4/(1.0+i+j)+0.01
randIndex = int(random.uniform(0,len(dataIndex)))
h = sigmod(sum(dataMatrix[randIndex]*weights))
error = float(classLabels[randIndex])-h
weights=weights + alpha*error*dataMatrix[randIndex]
return weights