茫然传输（Oblivious Transfer）

转自

1-out-2 OT

Oblivious Transfer（茫然传输）简称OT，是一种基本密码学原语，被广泛的用于安全多方计算等领域。
OT最早在1981年被 Michael O. Rabin提出[1]，在Rabin的OT协议中，发送者S发送一个信息m给接收者R，接收者R以1/2的概率接受信息m。所以在协议交互的结束的时候，S并不知道R是否接受了消息。该方案是基于RSA加密体系构造的。
1985年S. Even, O. Goldreich, and A. Lempel提出了1-out-2 OT[2],在新的方案中S每次发送2个信息$m_0$和$m_1$，而R每次输入一个选择b。当协议结束的时候，S无法获得关于b的任何有价值的信息，而R只能获得$m_b$，对于$m_{1-b}$，R也一无所知。

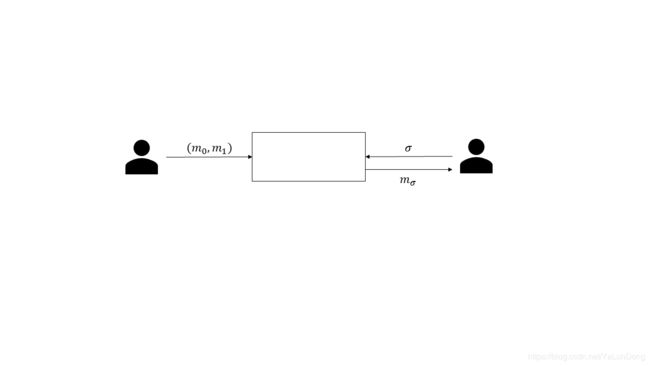
1988年，Claude Crépeau 证明了Rabin的OT方案和1-out-2 OT方案是等价的[3]。

1-out-n OT

而在1986年Brassard等人首次将1-out-2 OT扩展为1-out-n OT[4]，1998年Stern J P.首次将公钥特性加入了1-out-n OT协议之中[5]。

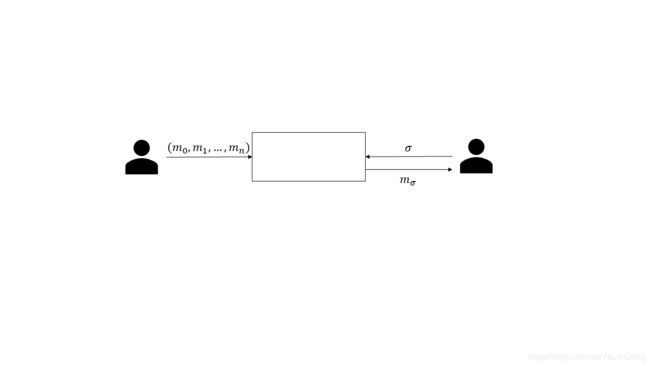
2001年Naor和Pinkas基于Diffie-Hellamn（DDH）困难问题假设给出了一个高效的2轮1-out-n OT协议[6]，同一年Aiello等人基于同态加密也给出了一个2轮的1-out-n OT协议[7]，并且在该方案中无论n多大，R只需要进行2次指数运算而S则需要2n 2n2n次指数运算。
2003年Yuval Ishai等人以1-out-2 OT为基础提出了一种高效的通过少量OT构造大量OT的方案，该方案基于随机神谕机构造[8]。
2008年，Lindell将cut-and-choose技术融入到OT协议中，给出了一个高效而且可以完全模拟的OT协议[9]。
2013年，Vladimir Kolesnikov1 和 Ranjit Kumaresan直接构造了1-out-n OT[19]，并且对于短消息的茫然传输效率比03年Yuval Ishai等人的方案更高。

浅见

在入门阶段，可以粗略看一下2000年之前的文章对于OT的起源和初始的想法有大体的了解。
对于[6] 和[7]的两篇文章可以着重看一下，其中对于安全性的证明和复杂性的分析是比较符合中等水平的要求的。
2003年和2013年的两篇论文可以对比看一下，很有意义也就很有意思。
2008年的论文作者Lindell是个大佬，牛到可以写算法导论那种等级著作的大佬，他在大作中的安全性证明不是写给一般水平玩家看的。
除此之外，还可以看一下Dan Bone的书[]中关于OT部分的介绍，比较浅显容易理解。

参考文献
[1]Michael O. Rabin. “How to exchange secrets by oblivious transfer.”
[2]S. Even, O. Goldreich, and A. Lempel, “A Randomized Protocol for Signing Contracts.”
[3]Claude Crépeau. “Equivalence between two flavours of oblivious transfer.”
[4]Gilles Brassard, Claude Crépeau and Jean-Marc Robert. “All-or-nothing disclosure of secrets.”
[5]Stern J P. “A New and Efficient All-Or-Nothing Disclosure of Secrets Protocol.”
[6]Moni Naor and Benny Pinkas. “Efficient oblivious transfer protocols.”
[7]Bill Aiello, Yuval Ishai, and Omer Reingold. “Priced Oblivious Transfer:How to Sell Digital Goods.”
[8]Ishai Y., Kilian J., Nissim K., Petrank E. “Extending Oblivious Transfers Efficiently.”
[9]Lindell Y. “Efficient Fully-Simulatable Oblivious Transfer.”
[10]Vladimir Kolesnikov and Ranjit Kumaresan. “Improved OT Extension for Transferring Short Secrets.”

敌手模型

半诚实（Semi-Honest）模型

假设参与计算的各方都是半诚实的，即参与方可以保留交互时得到的信息。对于想要协作完成计算并得到正确结果的参与方来说，这样的模型符合实际情况。

半诚实模型的敌手行为时被动的，它只是收集信息，这些信息可能用于以后的分析以图得到私有信息。

恶意（Malicious）模型

相对于半诚实模型，恶意的敌手拥有更主动的行为：

• 它可以拒绝参与协议的执行
• 可以用任意值来替换它的输入
• 可以在任意时间终止执行

Naor-Pinkas茫然传输协议

Naor和Pinkas通过三次公钥密码学操作实现了半诚实模型下的1-out-of-2茫然传输协议。
输入信息：

• Sender输入两个长度为l比特的字符串$(x_0,x_1)$
• Receiver输入一个选择比特r，用于选择$(x_0,x_1)$中的其中一个

系统参数：

• p,q均为素数，且q|p-1
• $Z_q$为q阶群，$G_q$是$Z_p^{\ast }$的q阶子群
• 给定$Z_p^{\ast }$的生成元g，满足Diffie-Hellman困难性假设

随机预言函数：

• H

协议：

• 步骤1
  S发送并公布随机数$C\in Z_q$，然后S生成随机数a，并计算$g^a$和$C^a$。
• 步骤2
  R选择随机数$1\le k\le q$，并生成公钥${pk}_r=g^k$，${pk}_{1-r}=C/g^k$，R将${pk}_0$发送给S。
• 步骤3
  S计算$({pk}_0{)}^a$，$({pk}_1{)}^a=C^a/({pk}_0{)}^a$。Sender将$(E_0,E_1)$发送给Receiver。$E_0=(g^a,H(({pk}_0{)}^a)\oplus x_0)$，$E_1=(g^a,H(({pk}_1{)}^a)\oplus x_1)$
• 步骤4
  Receiver通过计算$H((g^a{)}^k)$得到$H(({pk}_r{)}^a)$，因此可以得到
  $$x_r=E_{r,2}\oplus H(({pk}_r{)}^a)$$

扩展OT（OT Extension）

相对于对称密码学，基于数论中各种困难性假设的公钥密码学操作的算法复杂度更高。因此，在平时密文传输信息的过程中，通信双方都会先进行基于公钥密码学的密钥交换协议得到一个通信的对称密钥加密传输信息。

扩展OT的思路也一样。虽然这种方法没有完全抛弃公钥密码学操作，但是已经将公钥密码学操作的数量降低到很少。如，扩展OT可以将$O{T}_l^m$归约到使用少量基于公钥密码的$O{T}_{\lambda }^{\lambda }$和若干对称密码学操作，其中$\lambda <<m$。通常情况下，$\lambda$可以取为80，128或更多。注意$\lambda$不能太小，因为其通常作为安全性参数。

• 使用公钥密码学操作产生少量种子OT
• 利用堆成密码学操作（如PRG，哈希函数等）将这些种子OT协议扩展为任意数量的OT协力。

IKN茫然传输协议

Yuval Ishai等人提出的IKN茫然传输扩展协议，其中$\lambda$为安全参数

1. 1次$O{T}_l^m$协议->1次$O{T}_m^{\lambda }$协议
2. 1次$O{T}_m^{\lambda }$协议->$\lambda$次$O{T}_{\lambda }^1$协议。

注：下面展示Extending OT with a Semi-Honest Receiver

Part1: $O{T}_l^m$->$O{T}_m^{\lambda }$

输入信息：

• Sender有m对输入$(x_{j,0}，x_{j,1})$；$x$的长度为$l$位，$1\le j\le m$。
• Receiver有m个输入选择比特$\text{r}=(r_1,r2,...,r_m)$。

系统参数：

• 安全参数$\lambda$

随机预言函数：

• $\text{H}:[m]\times {\{0,1\}}^{\lambda }\to {\{0,1\}}^l$

协议：

1. S初始化一个随机向量$\text{s}\in {\{0,1\}}^{\lambda }$
2. R初始化一个$m\times \lambda$的随机矩阵$\text{T}$，其中${\text{t}}^i$代表$\text{T}$的第i列，${\text{t}}_i$代表$\text{T}$的第i行。
3. 进行$O{T}_m^{\lambda }$协议，在该协议中发送者为R而接收者为S，分别记为$R_S$及$S_R$。
   • $R_S$有$\lambda$对输入$({\text{t}}^i,\text{r}\oplus {\text{t}}^i)$
   • $S_R$有$\lambda$个输入选择比特$\text{s}$
   • $S_R$得到一个$m\times \lambda$的矩阵$\text{Q}$
4. S，即$S_R$，发送m对$(y_{j,0},y_{j,1})$给R，其中$y_{j,0}=x_{j,0}\oplus H(j,{\text{q}}_j)$；$y_{j,1}=x_{j,1}\oplus H(j,{\text{q}}_j\oplus \text{s})$；$1\le j\le m$
   ${\text{q}}_j=({\text{s}}_j\cdot {\text{r}}_j)\oplus {\text{t}}_j=\{\begin{array}{rlr}{t}_j& & r_j=0\\ s_j\oplus t_j& & r_j=1\end{array}$
5. R计算m个输出$z_j=y_{j,r_j}\oplus H(j,{\text{t}}_j)$；其中，$z_j=x_{j,r_j}$，$1\le j\le m$

重点分析4，5步

• 当$r_j=0$时，R收到$y_{j,0}=x_{j,0}\oplus H(j,t_j)$以及$y_{j,1}=x_{j,1}\oplus H(j,t_j\oplus s)$，而R只能解开$x_{j,0}$
• 当$r_j=1$时，R收到$y_{j,0}=x_{j,0}\oplus H(j,s_j\oplus t_j)$以及$y_{j,1}=x_{j,1}\oplus H(j,t_j)$，而R只能解开$x_{j,1}$

PART2 $O{T}_m^{\lambda }$->$O{T}_{\lambda }^{\lambda }$

思路：其实就是利用$O{T}_{\lambda }^{\lambda }$传输混淆元，后面与OT再无关系。后面通过随机预言函数基于长度为$\lambda$的混淆元生成长度为m的混淆项。

输入信息：

• Sender有对$\lambda$输入$(x_{i,0}，x_{i,1})$；$x$的长度为$m$位，$1\le i\le \lambda$。
• Receiver有$\lambda$个输入选择比特$\text{r}=(r_1,r2,...,r_{\lambda })$。

系统参数：

• 安全参数$\lambda$

随机预言函数：

• $\text{G}:{\{0,1\}}^{\lambda }\to {\{0,1\}}^m$

协议：

1. S初始化$\lambda$对随机的长度为k比特的$(s_{i,0},s_{i,1})$
2. 进行$O{T}_{\lambda }^{\lambda }$协议，在该协议中发送者为S而接收者为R，分别记为$S_S$及$R_R$。
   • $S_S$有$\lambda$对输入$(s_{i,0},s_{i,1})$
   • $S_R$有$\lambda$个输入选择$\text{r}$
   • $S_R$得到长度为$\lambda$的向量$\text{s}=\{s_{i,r_i}\}$；$1\le i\le \lambda$
3. S向R发送$\lambda$对$(y_{i,0},y_{i,1})$，其中$y_{i,0}=x_{i,b}\oplus \text{G}(s_{i,b})$
4. R通过步骤2中得到的向量$\text{s}$进行还原，即$z_i=y_{i,r_i}\oplus \text{G}(s_{i,r_i})$

PART3 $O{T}_{\lambda }^{\lambda }$可以通过调用$\lambda$次$O{T}_{\lambda }^1$协议实现

效率分析

• R共调用m次H，$2\lambda$次G，发送数据$2m\lambda$比特
• S共调用2m次H，$\lambda$次G，发送数据$2ml$比特
• 当然协议中调用了一次$O{T}_{\lambda }^{\lambda }$协议，因为与m和l无关为常数。

综上，整个流程归约到$O{T}_{\lambda }^{\lambda }$（只有该部分与公钥密码学相关），即相当于$\lambda$次$O{T}_{\lambda }^1$协议。