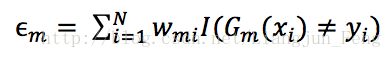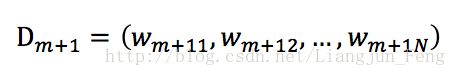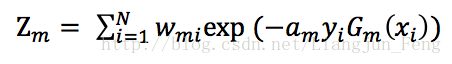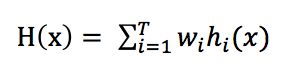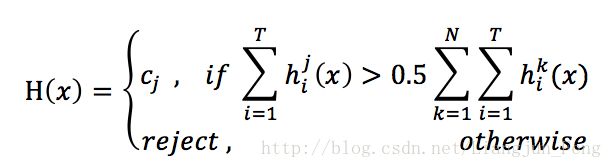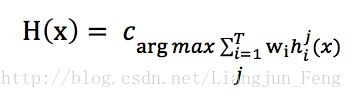机器学习教程 之 集成学习算法： 深入刨析AdaBoost

Boosting 是一族可以将弱学习器提升为强学习器的算法。这族算法的工作机制类似：先从初始训练集训练出一个基学习器，再根据基学习器的表现对训练样本分布进行调整，使得先前基学习器做错的训练样本在后续受到更多的关注，然后基于调整后的样本分布来训练下一个基学习器；如此重复进行，直至基学习器达到事先指定的值T，最终将这T个基学习器进行加权结合。

Boosting 族算法最著名的代表是AdaBoost
A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting
我之前写过一篇关于集成学习的文章,其中一篇是专门介绍了集成学习的两种框架实现
机器学习教程 之 Boosting 与 bagging：集成学习框架
以及这几篇关于GBDT和XGBoost的博客
机器学习教程 之 梯度提升方法：GBDT及其扩展模型XGBoost
机器学习教程 之 梯度提升方法：GBDT处理分类问题
机器学习教程 之 加性模型：GBDT退化为AdaBoost原理
还有一篇关于bagging随机森林的博文
机器学习教程 之 随机森林： 算法及其特征选择原理
这次开这篇博客会详细介绍AdaBoost的数学原理，包括一下几点

一、什么是集成学习？
二、AdaBoost算法
三、AdaBoost的python3实现（决策树桩为基分类器）
四、AdaBoost算法性能的影响因素
五、AdaBoost算法的优缺点
六、随机森林算法简介

一、什么是集成学习？

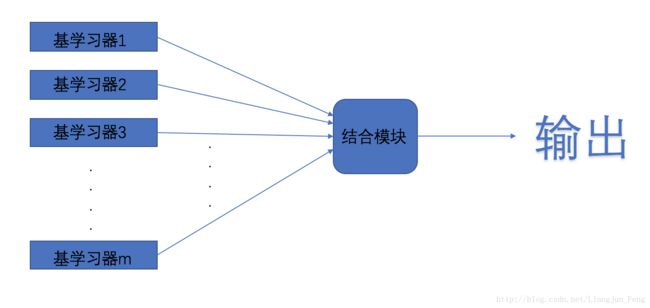
集成学习（ensemble learning）是机器学习算法当中的一类，它通过构建并结合多个学习器来完成学习任务，有时也被称为多分类器系统（multi-classifier system）

它的基本思路是：先产生一组“基学习器”，再使用某种策略将它们结合起来，基学习器通常是现有的学习算法，比如决策树、神经网络等、基学习器可以是相同的，也可以是不同的

不要把集成学习看作一些机器学习算法结果上简单的集成，因为使用同一个数据集去训练同一种分类器，即使训练很多个分类器，它们的分类结果也可能是十分相似的，对于最终的分类帮助也不会很大

集成学习对于基学习器有一个标准：
要获得好的集成结果，基学习器应当“好而不同”，即个体学习器要有一定的“准确性”，即学习器不能太坏，并且学习器的分类性能应当存在差异但事实上，基学习器都是为了解决同一个问题基于同一个训练集训练出来的，其“准确性”和“多样性”本身就存在一定的冲突，一般来说，准确性高了，增加多样性就需要牺牲准确性，如何产生并结合“好而不同”的基学习器是集成学习的核心问题

目前的集成学习算法可以根据基学习器的生成方式分为两类：
1） 基学习器采用串行生成的序列化方法，个体学习器之间存在强依赖关系，代表为Boosting算法群
2） 基学习器采用并行化的生成方法，不存在强依赖关系，可同时生成，其代表为随机森林（Random Forest）算法
这里我们将主要以Boosting算法中最成功，也是最具代表性的AdaBoost算法为例，说明集成学习的原理和特性，在结尾会稍微对随机森林算法有所介绍

二、AdaBoost算法

在介绍Adaboost算法之前，我先简单介绍一下Boosting算法，boosting起源于1988年Kearns在研究PAC（Probably Approximately Correct）模型时对Valiant提出的问题——“弱学习是否等于强学习？”

弱学习算法：指泛化性能略优于随机猜测的分类算法
强学习算法：识别准确率很高并且能在多项式时间内完成的学习算法

至1990年，Schapire最先对该问题给出了肯定的证明，提出了最初的Boosting 算法，该算法证明了弱学习算法可以被提升到1- a（置信度）概率输出错误率小于任意b（精度）的假设，即得到强学习算法

Boosting算法的证明中要求提前预知分类器错误率的上限，因此难以在实际问题中使用，Freund和Schapire为了改进Boosting算法的这一缺陷，于1995年提出了AdaBoost（Adaptive Boosting算法），这一算法提出，在机器学习领域受到了极大的关注，成为Boosting家族最具代表性的算法
在深度学习出现以前，Adaboost、随机森林还有支持向量机，几乎是当时性能最为优越的分类算法，即使是现在，Adaboost在图像识别、语音识别等领域也占有重要地位

AdaBoost算法流程：

1 初始化训练数据的权值分布，一开始每一个样本赋予相同的权值1/N

2）进行多轮的迭代学习，使用具有权值分布的Dm的训练数据集来学习，得到基本分类器。分对的样本的权值会降低，分错的样本的权值会增加，目的是使分错的训练样本得到更多的关注。每个学习器都会有一个权值am，am的值是基于每个弱分类器的错误率和权值分布进行计算的

学习器的权值为

m表示第几个学习器。从这个公式可以看出，当小于0.5时，am>0，意味着学习器的误差率越小，基学习器在最终的分类器中作用越大，然后我们还需要更新样本的权值分布

这样可以使得被级分类器Gm误分类样本的权值增大，而被正确分类样本的权值减小，其中Zm是规范化因子，可以使得Dm+1成为一个概率分布

3) 组合各弱学习器

得到的最终分类器为

sign(x)在x<0,x=0,x>0时分别取值为-1，0，1

AdaBoost的数学原理推导过程请见我的另一篇博客
人工智能里的数学修炼 | AdaBoost的数学原理： 分布更新推导
这里还有一些关于Boost与Bagging的集成学习框架的讲解
机器学习教程 之 Boosting 与 bagging：集成学习框架

三、AdaBoost的python3实现（决策树桩为基分类器）

接下来，使用决策树桩（即只有一层的决策树）作为基学习器，以皮马印第安糖尿病数据集作为学习对象，实现AdaBoost算法

皮马数据集介绍和下载地址
https://github.com/LiangjunFeng/Machine-Learning/blob/master/pima-indians-diabetes%20dataset

完整代码地址
https://github.com/LiangjunFeng/Machine-Learning/blob/master/6.AdaBoost.py

程序分段讲解，数据预处理

#!/usr/bin/env python3
# -*-coding: utf-8-*-
# Author : LiangjunFeng
# Blog : http://my.csdn.net/Liangjun_Feng
# GitHub : https://www.github.com/LiangjunFeng
# File : AdaBoost.py
# Date : 2017/09/17 11:12
# Version: 0.1
# Description: AdaBoost algorithm ,ensemble learning

import numpy
import math
from pandas import read_csv

def loadData():      #读取CSV格式数据文件
    dataSet = read_csv('/Users/zhuxiaoxiansheng/Desktop/data_set/pima-indians-diabetes/pima-indians-diabetes.csv',header = None)
    return dataSet

def dataPrepreocess(dataSet):   #数据预处理，将属性与标签分开，同时以中值填充缺少数据，将数据转化为矩阵格式
    dataSet[[0,1,2,3,4,5,6,7]] = dataSet[[0,1,2,3,4,5,6,7]].replace(0,numpy.NaN)
    data = dataSet[[0,1,2,3,4,5,6,7]]
    data.fillna(data.median(),inplace = True)              #以中值填充空白
    label = dataSet[8]         

    data = numpy.matrix(data.as_matrix(columns=None))      #转化为矩阵
    label = numpy.matrix(label.as_matrix(columns=None))    #转化为矩阵 

    return data,label.T

def dataSplit(data,label):      #将数据分为测试集和训练集
    for i in range(len(label)):
        if label[i,0] == 0:
            label[i,0] = -1
    mid = int(len(data)*0.68)    
    trainData = data[0:mid]     #前68%为训练集 
    testData = data[mid:]       #剩下的为测试集

    trainLabel = label[0:mid,0]
    testLabel = label[mid:,0]

    return trainData,trainLabel,testData,testLabel  #返回训练集、训练标签、测试集、测试标签

程序主体为两个类，决策树桩类与AdaBoost类

class decisionRoot:                                 #以决策树桩类作为基学习器
    def __init__(self):                     
        self._rootAttribute = 0                     #树根的分类属性
        self._thresholdValue = 0                    #分类属性的分类阈值
        self._minError = 0                          #存贮该分类器的分类误差
        self._operator = None                       #分类操作符，取值为‘le’或‘gt’
        self._estimateLabel = None                  #对训练样本的估计分类


    @classmethod
    def classify(cls,data,operator,thresholdValue):          #已知树根的分类属性、分类阈值、分类操作符后，用于实现样数据的二分类
        estimateLabel =  numpy.ones((data.shape[0],1))
        if operator == 'le':
            estimateLabel[data <= thresholdValue] = -1       #属性值小于等于阈值的样本标签设置为-1，其余的为1
        else:
            estimateLabel[data > thresholdValue] = -1        #属性值大于阈值的样本标签设置为-1，其余的为1
        return estimateLabel

    def buildTree(self,data,label,distribute):      #根据训练数据和样本分布训练取得最优分类树
        samples,attributes = data.shape
        estimateLabel = numpy.matrix(numpy.zeros((samples,1)))
        minError = numpy.inf                        #初始的最小误差为无限大
        stepNumber = 10.0                           #为决定属性的最优分类阈值，将样本的属性从最小值到最大值遍历，步数为10
        for rootAttribute in range(attributes):
            attributeMin = data[:,rootAttribute].min()
            attributeMax = data[:,rootAttribute].max()
            stepSize = (attributeMax - attributeMin)/stepNumber    #获得步长
            for j in range(int(stepNumber+1)):      #遍历属性，以求得最优分类属性
                for operator in ['le','gt']:        #选择操作符，获得最优操作符号
                    thresholdValue = attributeMin + j*stepSize     #分类阈值
                    estimateLabel = decisionRoot.classify(data[:,rootAttribute],operator,thresholdValue)      #估计标签
                    errLabel = numpy.matrix(numpy.ones((samples,1)))
                    errLabel[estimateLabel == label] = 0
                    error = float(distribute*errLabel)             #计算分类误差
                    if error < minError:
                        minError = error                           #将最小误差的参数记录
                        self._minError = minError
                        self._rootAttribute = rootAttribute
                        self._thresholdValue = thresholdValue
                        self._operator = operator
                        self._estimateLabel = estimateLabel.copy()

    def predict(self,data):                         #输入数据，预测结果
        samples = data.shape[0]
        result =  numpy.matrix(decisionRoot.classify(data[:,self._rootAttribute],self._operator,self._thresholdValue))
        return result


class AdaBoost:  
    def __init__(self):              
        self._rootNumber = 0               #训练分类树桩的数目
        self._decisionRootArray = []       #存储训练好的分类树桩
        self._alphaList = []               #分类树桩对应的alpha列表

    @classmethod
    def exp(cls,vector):                   #对向量里的所有成员使用exp函数
        for i in range(len(vector)):
            vector[i,0] = math.exp(vector[i,0])
        return vector

    def trainRoot(self,data,label,rootNumber = 41):     #串行训练树桩，并存储训练好的分类器
        samples,attributes = data.shape
        self._rootNumber = rootNumber
        distribute = numpy.matrix(numpy.ones((1,samples))/float(samples))
        for i in range(self._rootNumber):               #训练给定数目的基分类器
            root = decisionRoot()
            root.buildTree(data,label,distribute)       #建立分类树桩
            alpha = 0.5 * math.log((1.0 - root._minError)/max(root._minError,1e-16))
            self._alphaList.append(alpha)
            expValue = AdaBoost.exp(numpy.multiply(-1*alpha*label,root._estimateLabel))
            distribute = numpy.multiply(distribute,expValue.T)
            distribute = distribute/float(distribute.sum())            #更新分布 
            self._decisionRootArray.append(root)

    def vote(self,predictMatrix):          #投票法决定分类结果
        samples = predictMatrix[0].shape[0]
        result = []
        for i in range(samples):
            sign = 0
            for j in range(self._rootNumber):
                sign += predictMatrix[j][i,0] * self._alphaList[j]  #计算sign函数的输入值
            if sign >= 0:
                result.append(1)        
            else:
                result.append(-1)           #记录投票结果
        return result

    def predict(self,data):                #根据众多训练好的分类器，集成投票结果
        predictMatrix = []
        for i in range(self._rootNumber):  #遍历每一个分类器，得到分类值
            root = self._decisionRootArray[i]
            result = root.predict(data)
            predictMatrix.append(result)
        return numpy.matrix(self.vote(predictMatrix)).T       #返回各个分类器的投票结果

def assess(predictResult,actualLabel):      #评估分类器正确率
    count = 0
    for i in range(predictResult.shape[0]):
        if predictResult[i,0] == actualLabel[i,0]:
            count += 1
    return count/ float(predictResult.shape[0])

测试函数

if __name__ == '__main__': 
    dataSet = loadData()
    data,label = dataPrepreocess(dataSet)
    trainData,trainLabel,testData,testLabel = dataSplit(data,label) #获得训练集、测试集

    Ada = AdaBoost()           
    Ada.trainRoot(trainData,trainLabel)
    result = Ada.predict(testData)
    print(assess(result,testLabel))

代码运行结果，分类正确率为82.1%，之前用贝叶斯分类器分类结果正确率为70%，分类性能有明显提升
贝叶斯分类器判别皮马数据集
http://blog.csdn.net/liangjun_feng/article/details/78057753

四、AdaBoost算法性能的影响因素

4.1 结合策略

1）平均法
对数值型输出hi(x),最常见的结合策略是使用平均法，平均法又分为简单平均法和加权平均法，其公式可统一为

其中wi是基学习器的权重，通常要求wi >= 0,同时权重之和为1，简单平均法是加权平均法为wi = 1/T的特例。AdaBoost算法应用的就是这种加权平均法

2）投票法
对分类任务来说，学习器hi从类别标记集合{c1,c2,…,cN}中预测出一个标记，为方便讨论，我们将hi在样本x上的预测输出为一个N维向量

投票法有绝对多数投票法

即若某标记得票数过半，则预测为该标记；否则拒绝预测
相对多数投票法

即预测为得票最多的标记，若同时有多个标记获得最高票，则从中随机选取一个
加权投票法

与加权平均法类似，通常要求wi >= 0,同时权重之和为1

3）学习法
学习法相比于之前的两种方式较为复杂，需要先从初始数据集训练出初级学习器，然后“生成”一个新的数据集用于训练次级学习器，在这个新数据集中，初级学习器的输出被当作样例输入特征，而初始样本的标记仍被当作样例标记。这里不在过多赘述这种方法

4.2 多样性增强

1）数据样本扰动
给定数据集，可以从中产出不同的数据子集，再利用不同的数据子集训练出不同的个体学习器，数据样本扰动是基于采样法
数据样本扰动对于一些“不稳定的基学习器”较为有效，例如决策树、神经网络等等，训练样本稍加变化就会导致学习器有显著变动

2）输入属性扰动
训练样本通常由一组属性描述，不同子空间提供了数据的不同观察视角。显然，从不同子空间训练出的个体学习器必然有所不同，随机森林算法采用的就是这一策略

五、AdaBoost算法的优缺点

算法优点：
AdaBoost算法具有能够显著改善分类器预测精度、不需要先验知识、理论扎实等优点，但其更重要的意义在于为研究和解决实际问题带来了新的思想，在学大多数学习算法通过构造越来越复杂的分类器来提高预测精度时，AdaBoos却追求将最简单的、比随机猜测略好的弱分类器组合得到强分类器

算法缺点：
1） 对噪声数据敏感，Adaboost算法选择指数损失函数，这个函数过度的聚焦于始终难以被准确分类的样本，而这些样本通常是噪声和奇异值点，这一现象又会使分类器精度下降、出现“退化”问题
2） 与二分类问题相比，Boosting算法群的多分类理论并不完善，寻找更多适合多分类问题的损失函数，以及多分类下的精确弱分类条件都是值得继续研究的问题

六、随机森林算法简介

随机森林（Random Forest，RF）在以决策树为基学习器的基础上，进一步在决策树的训练过程中引入了随机属性选择。具体来说，传统决策树在选择划分属性时是在当前结点的属性集合（假定有d个属性）中选择一个最优属性；而在RF中，对基决策树的每个结点，先从该结点的属性集合中随机选择一个包含k个属性的子集，然后再从这个子集中选择一个最优属性用于划分，这里的参数k控制了随机性的引入程度。
随机森林简单、容易实现、计算开销小，令人惊奇的是，它在很多现实任务中展现出强大的性能，被誉为“代表集成学习技术水平的方法”。