周志华《机器学习》学习笔记——Logistic回归

前言

  《周志华《机器学习》学习笔记——线性回归》这篇文章介绍了线性回归，线性回归模型虽然简单，但却有着丰富的变化。例如对于样例 (x,y),y∈R ，当我们希望线性模型的预测值逼近真是标记 y 时，就得到了线性回归模型。

y=wTx+b

从回归到分类

  需要注意的是Logistic回归实际上是一种分类模型。上面讨论了如何使用线性模型进行回归学习，但若要做的是分类任务该怎么办呢？此时只需找到一个函数将分类任务的真是标记 y 与线性回归模型的预测值联系起来。

  考虑二分类任务，其输出标记 y∈{0,1} ，而线性回归模型产生的预测值 z=wTx+b ， z∈[−∞,+∞] 是连续值，于是，我们需要将连续值 z 转换为0/1值。最理想的是“单位阶跃函数”（unit-step function）

y=⎧⎩⎨⎪⎪0,z<00.5,z=01,z>0

即若预测值 z 大于零就判为正例，小于零就判为负例，预测值为临界值零则可任意判别，下图绘出了单位阶跃函数和对数几率函数
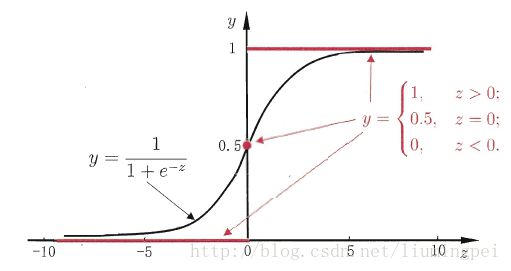
  从上图可以看出，单位阶跃函数不可导，而我们在模型求解的步骤中会对出现 y 对 z 的导数，这样单位阶跃函数就不可用了。于是我们希望找到能在一定程度上近似单位阶跃函数的“替代函数”，并希望它单调可微。对数几率函数（简称“对率函数”）正是这样一个常用的替代函数

y=11+e−z

  对数几率函数是一种“Sigmoid函数”，它将 z 值转化为一个接近0或1的 y 值，并且其输出值在 z=0 附近变化很陡。对数几率函数有个非常好的性质，就是它是任意阶可导的函数。

Logistic回归

  将对数几率函数作为判别函数代入到线性回归模型中，得到

y=11+e−(wTx+b)

   Logistic函数实现了任意实数到[0,1]的映射，这样我们的数据集 (x1,x2,...,xn) ，不管其输出 y 是大于1或者小于0，都可以映射到 [0,1] 区间进行分类。 实际上y给出了输出为1的概率，比如当 y=0.8 ，那么说明有80%的概率输出为1。输出为0的概率是输出为1的补集，也就是20%。
   若将 y 视为样本 x 作为正例的可能性，则 1−y 是其反例可能性，两者的比值

y1−y

称为“几率”（odds），反映了 x 作为正例的相对可能性。对几率取对数则得到“对数几率”（log odds，也称logit）

lny1−y=wTx+b

   由此可以看出，上式实际上是在用线性回归模型的预测结果去逼近真实标记的对数几率，因此，其对应的模型称为“对数几率回归”（logistic regression）。需要注意的是，虽然它的名字是“回归”，但实际确实一种分类方法。这种方法有很多优点：

1. 它是直接对分类可能性进行建模，无需事先假设数据分布，这样就避免了假设分布不准确所带来的问题；
2. 它不是仅预测出“类别”，二是可得到近似概率预测，这对许多需利用概率辅助决策的任务很有用；

3. 对数几率函数是任意阶可导的凸函数，有很好的数学性质，现有的许多数值优化算法都可以直接用于求取最优解，例如梯度下降法、拟牛顿法等。

      如果我们有合适的参数 w 和 b ，那么我们对样本 x 分类就可以通过上述公式计算出一个概率，如果这个概率大于0.5，我们就可以说样本是正样本，否则样本是负样本。举个例子，对于判断西瓜是否成熟的应用场景，对于给定的西瓜，我们定义成熟西瓜为正样本，生瓜为负样本。我们通过计算出的概率值即可判断西瓜是否成熟。
     下面我们来看看如何确定 w 和 b 。若将 y 视为类后验概率估计 p(y=1|x) ，则有

   lnp(y=1|x)p(y=0|x)=wTx+b
   
   简单起见，我们令
   hw(x)=11+e−(wTx+b)
   
   显然有
   p(y=1|x;w,b)=hw(x)=ewTx+b1+ewTx+b
   p(y=0|x;w,b)=1−hw(x)=11+ewTx+b
   上式即为在已知样本 x 和参数 w 和 b 的情况下，样本 x 属于正样本（ y=1 ）和负样本（ y=0 ）的条件概率。理想情况下，求出各个点的概率都为1，也就是所有点都分类正确。但是考虑到实际情况，求出的概率不可能完全等于1，这时候样本点的概率越接近1，分类效果就越好。比如一个样本属于正样本的概率为0.51，那么我们就可以说明这个样本属于正样本。另一个样本属于正样本的概率为0.99，那么我们也可以说明这个样本属于正样本。但是显然，第二个样本概率更高，更具说服力。我们可以把上述两个概率公式合二为一
   Cost(hw(x),y)=hw(x)y(1−hw(x))(1−y)
   
   合并出来的 Cost ，我们称之为代价函数。当 y=1 时，后面一项为零；当 y=0 时，前面一项为零。为了简化问题，我们对整个表达式求对数
   Cost(hw(x),y)=ylnhw(x)+(1−y)ln(1−hw(x))
   
     这个代价函数是对一个样本而说的，给定一个样本，通过这个公式就能求出样本所属类别的概率，而这个概率越大越好，所以也就是求解这个代价函数的最大值。这只是对一个样本来说的，而样本集的代价函数之和只需要将所有样本的代价函数累加即可，因此整个样本集的生成概率为
   J(w)=∑i=1m[y(i)ln(hw(xi))+(1−y(i))ln(1−hw(x(i)))]
   
     求 J(w) 的极大值等价于求 −J(w) 的最小值，注意到 J(w) 是关于 w 的高阶可导连续凸函数，根据凸优化理论，经典的数值优化算法如梯度下降法、牛顿法等都可以求得其最优解。这里我们以梯度下降法为例，求 J(w) 的极小值。

梯度下降法

梯度下降算法

模型求解

   既然已经知道了梯度下降算法的原理，下面我们就用该算法来求Logistic回归模型的参数，为方便起见，令 β=(w;b) ， xˆ=(x;1) ，则 wTx+b 可简写为 βxˆ 。求 −J(β) 的极小值，更新公式可以这样写

βj:=βj+α∂J(β)∂βj

:= 是赋值的意思，简单起见，这里我们还用 J(β) ，而不用其相反数，只需要将步长 α 取为负数即可，现在我们已经知道

J(β)=∑i=1m[y(i)ln(hβ(xˆi))+(1−y(i))ln(1−hβ(xˆ(i)))]

Sigmoid函数为

hβ(xˆ)=11+e−βxˆ

   现在，我们只需要求出 J(β) 对 βj 的偏导数，即可利用梯度下降法，求解 J(β) 的极小值了。
J(β) 对 βj 的偏导数求解过程如下：

∂J(β)∂βj=∂J(β)∂hβ(xˆ)×∂hβ(xˆ)∂βxˆ×∂βxˆ∂βj

其中第一项

∂J(β)∂hβ(xˆ)=y×1hβ(xˆ)+(y−1)11−hβ(xˆ)

第二项是对率函数的求导公式

∂hβ(xˆ)∂βxˆ=hβ(xˆ)(1−hβ(xˆ))

最后一项

∂βxˆ∂βj=∂(β1xˆ1+β2xˆ2+...+βnxˆn)∂βj=xˆj

因此梯度下降迭代公式为

βj:=βj+α(y(i)−hβ(xˆ(i)))xˆ(i)j

   知道了，梯度下降迭代公式，我们就可以计算最佳拟合参数了。