线性模型——机器学习(周志华)

C++实现线性回归

线性模型

$$f(\mathbf{x})={\omega }_1{x}_1+{\omega }_2{x}_2+{\omega }_3{x}_3+...+{\omega }_d{x}_d+b$$
$$f(\mathbf{x})={\mathbf{\omega }}^{\mathbf{T}}\mathbf{x}+b$$

其中$\mathbf{\omega }=({\omega }_1;{\omega }_2;{\omega }_3;....;{\omega }_d)，\mathbf{x}=(x_1;x_2;...;x_d{)}^T$

线性回归

线性回归试图学得

$$f({\mathbf{x}}_{\mathbf{i}})=\mathbf{\omega }{\mathbf{x}}_{\mathbf{i}}+b$$

使得

$$f({\mathbf{x}}_{\mathbf{i}})\simeq y_i$$

如何求得$\omega$和$b$，关键在于衡量$f({\mathbf{x}}_{\mathbf{i}})\simeq y_i$，他们之间相差越小，结果越好，于是有

$$({\omega }^{\ast },b^{\ast })=\underset{\mathbf{\omega },b}{\arg }min\sum _{i=1}^m(f({\mathbf{x}}_{\mathbf{i}})-y_i{)}^2=\underset{\mathbf{\omega },b}{\arg }min\sum _{i=1}^m(y_i-\mathbf{\omega }{\mathbf{x}}_{\mathbf{i}}-b{)}^2$$
化为一般式：
$${\mathbf{\omega }}^{\ast }=\underset{\mathbf{\omega }}{\arg }min(\mathbf{y}-\mathbf{X}\mathbf{\omega }{)}^T(\mathbf{y}-\mathbf{X}\mathbf{\omega })$$

对上式的$\mathbf{\omega }$和$b$求导，当${\mathbf{X}}^{\mathbf{T}}\mathbf{X}$为满秩矩阵或者正定矩阵式，令其等于零得到

$${\mathbf{\omega }}^{\ast }=({\mathbf{X}}^{\mathbf{T}}\mathbf{X}{)}^{-1}{\mathbf{X}}^{\mathbf{T}}\mathbf{y}$$

最后求的线性回归模型为：

$$f({\mathbf{x}}_i)={\mathbf{x}}_i({\mathbf{X}}^{\mathbf{T}}\mathbf{X}{)}^{-1}{\mathbf{X}}^{\mathbf{T}}\mathbf{y}$$

m为数据集个数，d为属性个数，其中$\mathbf{X}$为$(m\ast d)$, $\mathbf{y}$为$(m\ast 1)$

现实中${\mathbf{X}}^{\mathbf{T}}\mathbf{X}$往往不是满秩矩阵，会出现列数对于行数，${\mathbf{X}}^{\mathbf{T}}\mathbf{X}$显然不满秩，此时可解出多个$\mathbf{\omega }$, 他们都能使均方误差最小化，选择哪一个解作为输出，将有学习算法的归纳偏好决定，常见的做法是引入正则化项。

也可模型预测值逼近y的衍生物，比如示例所对应的输出标记是在指数尺度上的变化，那么可以将输出标记的对数作为线性模型逼近的目标：
$$lny={\mathbf{\omega }}^{\mathbf{T}}\mathbf{x}+b$$
这就是“对数线性回归”。

更一般的，考虑单调可微函数。令

$$y=g^{-1}({\mathbf{\omega }}^{\mathbf{T}}\mathbf{x}+b)$$

这样得到的模型成为“广义线性模型”。

对数几率回归（逻辑回归）

上面讨论了使用线性模型进行回归学习，但如果要做的时分类任务该如何？我们现在讨论二分类。

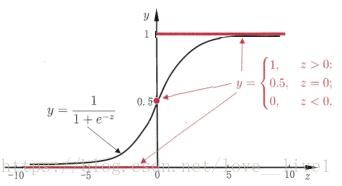
这时候就用到逻辑回归，与线性回归不一样的是，再线性回归($z={\mathbf{\omega }}^{\mathbf{T}}\mathbf{x}+b$)的基础上，外面包装了一个“sigmod”函数$y=\frac{1}{1+e^{-z}}$，函数图像如下。

若预测值z大于零判为正例，小于零判为负例，预测值为临界值则可任意判别。

1. 将z带入sigmod函数，得$y=\frac{1}{1+e^{-({\mathbf{\omega }}^{\mathbf{T}}\mathbf{x}+b)}}$
2. 然后化为 $ln\frac{y}{1-y}={\mathbf{\omega }}^{\mathbf{T}}\mathbf{x}+b$
3. 若将$y$视为$x$作为正例的可能性，则$1-y$是其反例的可能性，两者的比值成为“几率”。

接下去的看逻辑回归

线性判别分析（LDA）

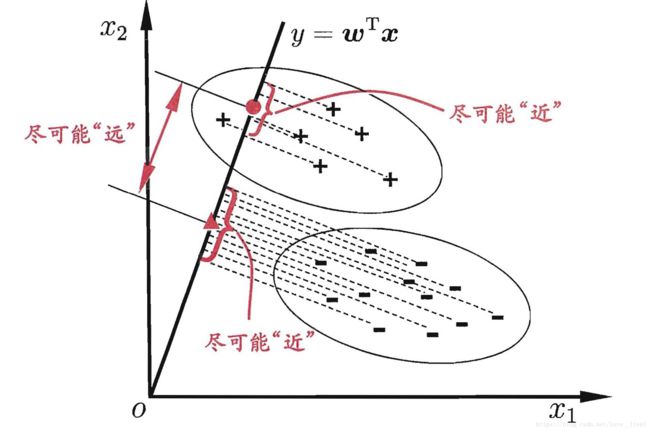
LDA的思想：给定训练集，设法将样例投影到一条直线上，是的同样类例的投影点尽可能接近、异类投影点尽可能远离；再对新样本进行分类时，将其同样投到这条直线上，再根据投影点的位置确定新样本的类别。

令$X_i、{\mu }_i、{\sum }_i$分别代表第$i\in \{0,1\}$类示例的集合、均值向量、协方差矩阵

• 两类样本的中心在直线上的投影分别为${\omega }^T{\mu }_0$和${\omega }^T{\mu }_1$;
• 若将所有样本点都投影到直线上，则两类样本的协方差分别为${\omega }^T{\sum }_0\omega$和${\omega }^T{\sum }_1\omega$;
• 我们的目的是${\omega }^T{\sum }_0\omega +{\omega }^T{\sum }_1\omega$尽可能小，使$||{\omega }^T{\mu }_0-{\omega }^T{\mu }_1|{|}_2^2$尽可能大;

$$\mathbf{J}=\frac{||{\mathbf{\omega }}^{\mathbf{T}}{\mathbf{\mu }}_0-{\mathbf{\omega }}^{\mathbf{T}}{\mathbf{\mu }}_1|{|}_2^2}{{\mathbf{\omega }}^{\mathbf{T}}{\sum }_0\mathbf{\omega }+{\mathbf{\omega }}^{\mathbf{T}}{\sum }_1\mathbf{\omega }}=\frac{{\mathbf{\omega }}^{\mathbf{T}}({\mathbf{\mu }}_0-{\mathbf{\mu }}_1)({\mathbf{\mu }}_0-{\mathbf{\mu }}_1{)}^{\mathbf{T}}\mathbf{\omega }}{{\mathbf{\omega }}^{\mathbf{T}}({\sum }_0+{\sum }_1)\mathbf{\omega }}$$

• 定义类内散度矩阵
  $${\mathbf{S}}_{\mathbf{w}}=\sum _0+\sum _1=\sum _{\mathbf{x}\in {\mathbf{X}}_0}(\mathbf{x}-{\mathbf{\mu }}_0)(\mathbf{x}-{\mathbf{\mu }}_0{)}^{\mathbf{T}}+\sum _{\mathbf{x}\in {\mathbf{X}}_0}(\mathbf{x}-{\mathbf{\mu }}_1)(\mathbf{x}-{\mathbf{\mu }}_1{)}^{\mathbf{T}}$$
• 定义类间散度矩阵
  $${\mathbf{S}}_{\mathbf{b}}=({\mathbf{\mu }}_0-{\mathbf{\mu }}_1)({\mathbf{\mu }}_0-{\mathbf{\mu }}_1{)}^{\mathbf{T}}$$
  $$\mathbf{J}=\frac{{\mathbf{\omega }}^{\mathbf{T}}{\mathbf{S}}_{\mathbf{b}}\mathbf{\omega }}{{\mathbf{\omega }}^{\mathbf{T}}{\mathbf{S}}_{\mathbf{w}}\mathbf{\omega }}$$
• 确定$\mathbf{\omega }$
  $$\begin{gathered} \mathbf{m}\mathbf{i}{\mathbf{n}}_{\mathbf{\omega }}-{\mathbf{\omega }}^{\mathbf{T}}{\mathbf{S}}_{\mathbf{b}}\mathbf{\omega } \\ s.t.{\mathbf{\omega }}^{\mathbf{T}}{\mathbf{S}}_{\mathbf{w}}\mathbf{\omega }=1 \end{gathered}$$
• 由拉格朗日乘子法，得
  $${\mathbf{S}}_{\mathbf{b}}\mathbf{\omega }=\mathbf{\lambda }{\mathbf{S}}_{\mathbf{\omega }}\mathbf{\omega }$$
• ${\mathbf{S}}_{\mathbf{b}}\mathbf{\omega }$的方向恒为${\mathbf{\mu }}_0-{\mathbf{\mu }}_1$，令
  $${\mathbf{S}}_{\mathbf{b}}\mathbf{\omega }=\mathbf{\lambda }({\mathbf{\mu }}_0-{\mathbf{\mu }}_1)$$
• 于是带入得
  $$\mathbf{\omega }={\mathbf{S}}_{\mathbf{\omega }}^{-1}({\mathbf{\mu }}_0-{\mathbf{\mu }}_1)$$

多分类学习

不失一般性，考虑N 个类别C1 ， C2 ，… ， CN ， 多分类学习的基本思路是"拆解法飞即将多分类任务拆为若干个二分类任务求解.具体来说，先对问题进行拆分，然后为拆出的每个二分类任务训练一个分类器;在测试时，对这些分类器的预测结果进行集成以获得最终的多分类结果。这里的关键是如何对多分类任务进行拆分，以及如何对多个分类器进行集成。

最经典的拆分策略有三种. “一对一” (One vs. One，简称OvO) 、“一对多” (One vs. Rest ，简称OvR)和"多对多" (Many vs. Many，简称MvM).

类别不平衡

加入有998个反例，2个正例，那么学习方法只需要放回一个永远将新样本预测为反例的学习器，就能达到99.8%的精度。

解决办法：

1. 对数据过多的一方进行欠采样
2. 对数据过少的一方进行过采样
3. 基于原始数据集进行学习，但是在用训练好的分类器进行预测时，加入一个策略到其决策过程，成为“阈值移动”。
   $$\frac{y^{{}^{\prime }}}{1-y^{{}^{\prime }}}=\frac{y}{1-y}\ast \frac{m^{-}}{m^{+}}$$

$m^{-}、m^{+}$分别为正反例数目