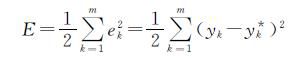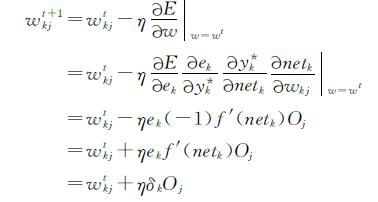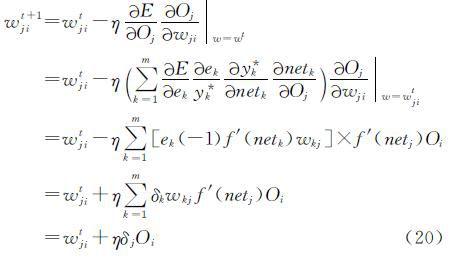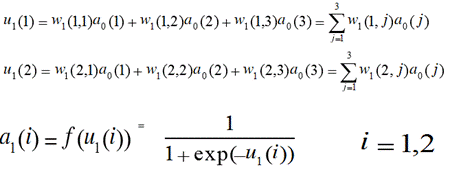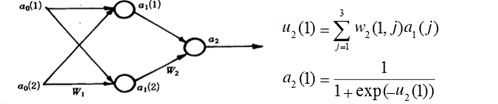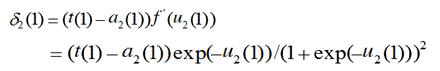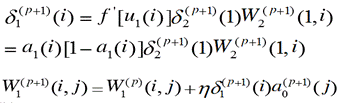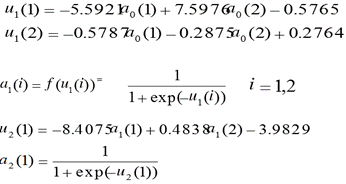BP神经网络(推荐)
神经网络由大量的节点(或称神经元)之间相互联接构成,每个节点代表一种特定的输出函数,称为激活函数(activation function);每两个节点间的连接都代表一个对于通过该连接信号的加权值,称之为权重(weight),神经网络就是通过这种方式来模拟人类的记忆。网络的输出则取决于网络的结构、网络的连接方式、权重和激活函数。而网络自身通常都是对自然界某种算法或者函数的逼近,也可能是对一种逻辑策略的表达,是对传统逻辑学演算的进一步延伸。
人工神经网络中,神经元处理单元可表示不同的对象,例如特征、字母、概念,或者一些有意义的抽象模式。网络中处理单元的类型分为三类:输入单元、输出单元和隐单元。输入单元接受外部世界的信号与数据;输出单元实现系统处理结果的输出;隐单元是处在输入和输出单元之间,不能由系统外部观察的单元。神经元间的连接权值反映了单元间的连接强度,信息的表示和处理体现在网络处理单元的连接关系中。
算法背景和发展
20世纪40年代,人们开始对神经网络研究。
1943 年,美国心理学家麦克洛奇(Mcculloch)和数学家皮兹(Pitts)提出了M-P模型,此模型比较简单,但是意义重大。在模型中,通过把神经元看作功能逻辑器件来实现算法,从此开创了神经网络模型的理论研究。
1949心理学家赫布(Hebb)提出Hebb法则,为构造有学习功能的神经网络模型奠定了基础。
1957 年,罗森勃拉特(Rosenblatt)以M-P 模型为基础,提出了感知器(Perceptron)模型;
1959年,美国著名工程师威德罗(B.Widrow)和霍夫(M.Hoff)等人提出ADALINE网络模型,ADALINE网络模型是一种连续取值的自适应线性神经元网络模型,可以用于自适应系统。
1972年,芬兰的KohonenT.教授,提出了自组织神经网络SOM(Self-Organizing feature map)。
1976年,美国Grossberg教授提出了著名的自适应共振理论ART(Adaptive Resonance Theory),其学习过程具有自组织和自稳定的特征。
1982年,美国物理学家霍普菲尔德(Hopfield)提出了一种离散神经网络,即离散Hopfield网络,从而有力地推动了神经网络的研究;
1984年,Hinton与年轻学者Sejnowski等合作提出了Boltzmann机模型;
1986年,儒默哈特(D.E.Ru melhart)等人在多层神经网络模型的基础上,提出了多层神经网络权值修正的反向传播学习算法----BP算法(Error Back-Propagation);
1988年,Chua和Yang提出了细胞神经网络(CNN)模型;
1994年,廖晓昕关于细胞神经网络的数学理论与基础的提出,带来了这个领域新的进展。通过拓广神经网络的激活函数类,给出了更一般的时滞细胞神经网络(DCNN)、Hopfield神经网络(HNN)、双向联想记忆网络(BAM)模型;
目录
反向传播模型也称B-P模型,是一种用于前向多层的反向传播学习算法。之所以称它是一种学习方法,是因为用它可以对组成前向多层网络的各人工神经元之间的连接权值进行不断的修改,从而使该前向多层网络能够将输入它的信息变换成所期望的输出信息。之所以将其称作为反向学习算法,是因为在修改各人工神经元的连接权值时,所依据的是该网络的实际输出与其期望的输出之差,将这一差值反向一层一层的向回传播,来决定连接权值的修改。
B-P算法的网络结构是一个前向多层网络,其基本思想是,学习过程由信号的正向传播与误差的反向传播两个过程组成。正向传播时,输入样本从输入层传入,经隐含层逐层处理后,传向输出层。若输出层的实际输出与期望输出不符,则转向误差的反向传播阶段。误差的反向传播是将输出误差以某种形式通过隐层向输入层逐层反传,并将误差分摊给各层的所有单元,从而获得各层单元的误差信号,此误差信号即作为修正各单元权值的依据。这种信号正向传播与误差反向传播的各层权值调整过程,是周而复始地进行。权值不断调整过程,也就是网络的学习训练过程。此过程一直进行到网络输出的误差减少到可以接受的程度,或进行到预先设定的学习次数为止。
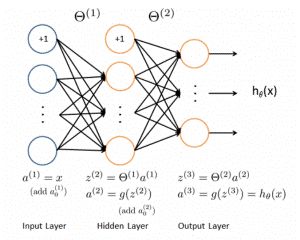
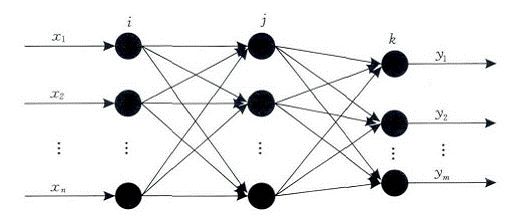
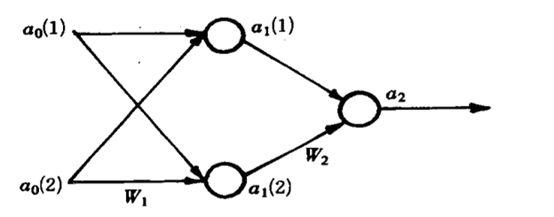
BP网络的拓扑结构包括输入层、隐层和输出层,它能够在事先不知道输入输出具体数学表达式的情况下,通过学习来存储这种复杂的映射关系.其网络中参数的学习通常采用反向传播的策略,借助最速梯度信息来寻找使网络误差最小化的参数组合.常见的3层BP网络模型如图所示.
其中,各节点的传递函数f必须满足处处可导的条件,最常用的为Sigmoid函数,第i个神经元的净输入为nwti,输出为Oi.如果网络输出层第k个神经元的期望输出为yk*,则网络的平方型误差函数为
由于BP算法按照误差函数E的负梯度修改权值,故权值的更新公式可表示为
其中,t表示迭代次数, 对于输出层神经元权值的更新公式为:
其中,δk称作输出层第k 个神经元的学习误差.对隐含层神经元权值的更新公式为:
其中,δj称作隐含层第j个神经元的学习误差.BP的误差反向传播思想可以概括为:利用输出层的误差来估计出其直接前导层的误差,再借助于这个新的误差来计算更前一层的误差,按照这样的方式逐层反传下去便可以得到所有各层的误差估计。
2相关应用应用领域:神经网络克服了传统人工智能方法对于直觉的缺陷,因而在神经专家系统、模式识别、智能控制、组合优化、预测等领域有成功的应用。
3参考资料1. Widrow B,Lehr M.30years of adaptive neural networks:Perceptron,madaline, and backpropagation.Proceedings of the IEEE,1990,78(9):1415-1442;
2. 焦李成,杨淑媛,刘芳,王士刚,冯志玺 神经网络七十年:回顾与展望吗,计算机学 报,2016,8(39):1697-1716;
3. 百度
4. 维基百科
5. 马克威分析系统使用教程,www.tenly.com.
4参考案例1.训练样本
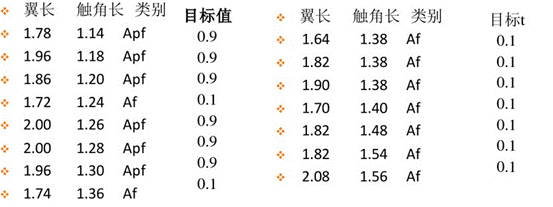
已知的两类蚊子的数据如下图
确定模型输入/输出结构:两输入、单输出
输入数据有15个,即p=1,2,……,15;j=1,2;对应15个输出。 建模:
(输入层、中间层、输出层、每层应选取多少个元素?) 建立神经网络
规定目标为: 当t(1)=0.9 时表示属于Apf类,规定目标为: 当t(1)=0.9 时表示属于Apf类。
具体训练步骤如下: 令p=0,p为样本编号 (1) 网络初始化
给各连接权值分别赋一个区间(0,1)内的随机数,设定误差函数E,给定计算精度值和最大学习次数M。
其中,![]() 表示第i层第j个神经元的阈值。
表示第i层第j个神经元的阈值。
(2)根据输入数据计算网络输出,取![]() ,将各个神经元的阈值作为固定值输入。
,将各个神经元的阈值作为固定值输入。
同理,输出神经元:
(3) 训练输出单元的权值
取学习速率η=0.1(或其他正数,可调整大小),计算![]() ,其中p为第p个样本,j=1,2,3…..
,其中p为第p个样本,j=1,2,3…..
(4) 训练隐藏单元的权值
PS:利用隐含层各神经元的误差项![]() 和输入层各神经元的输入来修正权值
和输入层各神经元的输入来修正权值
上述4个步骤为:使用第一个样本调整输出层和隐藏层各个神经元的权值
(5) 计算全局误差
当用完所有样本时,判断网络误差是否满足要求。
当误差达到预设精度或学习次数大于预
设最大次数,则结束算法。否则,返回(2),进入下一圈学习。
注:仅计算一圈(p=1,2,…,15)往往是不够的,直到误差达到预设精度或学习次数大于设定的最大次数时停止。本例中,共计算了147圈,迭代了2205次。 最后计算结果是:
网络模型的解为:
A、输入量的选择:
a、输入量必须选择那些对输出影响大且能够检测或提取的变量;
b、各输入量之间互不相关或相关性很小。从输入、输出量性质分类来看,可以分为两类:数值变量和语言变量。数值变量又分为连续变量或离散变量。如常见的温度、压力、电压、电流等就是连续变量;语言变量是用自然语言表示的概念。如红、绿、蓝;男、女;大、中、小、开、关、亮、暗等。一般来说,语言变量在网络处理时,需要转化为离散变量。
c、输入量的表示与提取:多数情况下,直接送给神经网络的输入量无法直接得到,常常需要用信号处理与特征提取技术从原始数据中提取能反映其特征的若干参数作为网络输入。
B、输出量选择与表示:
a、输出量一般代表系统要实现的功能目标,如分类问题的类别归属等;
b、输出量表示可以是数值也可是语言变量;
6相关条目感知机,人工神经网络,有监督学习,隐含层
7优缺点优点:理论基础牢固,推导过程严谨,物理概念清晰,通用性好等。所以,它是目前用来训练前向多层网络较好的算法。
缺点:(1)该学习算法的收敛速度慢;(2)网络中隐节点个数的选取尚无理论上的指导;(3)从数学角度看,B-P算法是一种梯度最速下降法,这就可能出现局部极小的问题。当出现局部极小时,从表面上看,误差符合要求,但这时所得到的解并不一定是问题的真正解。所以B-P算法是不完备的。
BP算法局限性:
(1)在误差曲面上有些区域平坦,此时误差对权值的变化不敏感,误差下降缓慢,调整时间长,影响收敛速度。这时误差的梯度变化很小,即使权值的调整量很大,误差仍然下降很慢。造成这种情况的原因与各节点的净输入过大有关。
(2)存在多个极小点。从两维权空间的误差曲面可以看出,其上存在许多凸凹不平,其低凹部分就是误差函数的极小点。可以想象多维权空间的误差曲面,会更加复杂,存在更多个局部极小点,它们的特点都是误差梯度为0。BP算法权值调整依据是误差梯度下降,当梯度为0时,BP算法无法辨别极小点性质,因此训练常陷入某个局部极小点而不能自拔,使训练难以收敛于给定误差。
BP算法改进:误差曲面的平坦区将使误差下降缓慢,调整时间加长,迭代次数增多,影响收敛速度;而误差曲面存在的多个极小点会使网络训练陷入局部极小,从而使网络训练无法收敛于给定误差。这两个问题是BP网络标准算法的固有缺陷。
针对此,国内外不少学者提出了许多改进算法,几种典型的改进算法:
(1)增加动量项:标准BP算法在调整权值时,只按t时刻误差的梯度下降方向调整,而没有考虑t时刻以前的梯度方向,从而常使训练过程发生振荡,收敛缓慢。为了提高训练速度,可以在权值调整公式中加一动量项。大多数BP算法中都增加了动量项,以至于有动量项的BP算法成为一种新的标准算法。
(2)可变学习速度的反向传播算法(variable learning rate back propagation,VLBP):多层网络的误差曲面不是二次函数。曲面的形状随参数空间区域的不同而不同。可以在学习过程中通过调整学习速度来提高收敛速度。技巧是决定何时改变学习速度和怎样改变学习速度。可变学习速度的VLBP算法有许多不同的方法来改变学习速度。
(3)学习速率的自适应调节:可变学习速度VLBP算法,需要设置多个参数,算法的性能对这些参数的改变往往十分敏感,另外,处理起来也较麻烦。此处给出一简洁的学习速率的自适应调节算法。学习率的调整只与网络总误差有关。学习速率η也称步长,在标准BP中是一常数,但在实际计算中,很难给定出一个从始至终都很合适的最佳学习速率。从误差曲面可以看出,在平坦区内η太小会使训练次数增加,这时候希望η值大一些;而在误差变化剧烈的区域,η太大会因调整过量而跨过较窄的“凹坑”处,使训练出现振荡,反而使迭代次数增加。为了加速收敛过程,最好是能自适应调整学习率η,使其该大则大,该小则小。比如可以根据网络总误差来调整.
(4)引入陡度因子----防止饱和:误差曲面上存在着平坦区。其权值调整缓慢的原因在于S转移函数具有饱和特性造成的。如果在调整进入平坦区后,设法压缩神经元的净输入,使其输出退出转移函数的饱和区,就可改变误差函数的形状,从而使调整脱离平坦区。实现这一思路的具体作法是在转移函数中引进一个陡度因子。
以上转自:http://www.markwaymall.com网,下面给出python实现:
待续……