人工智能算法(一)进化算法
我希望用这类文章,来尽可能通俗的解释一些听上去很“高大上”的人工智能算法,不仅可以帮助自己真正的理解,还能带来更多的思考。目前想写专家系统,神经网络,还有本篇进化算法。
不说大话,进入正题:
相信大部分对人工智能感兴趣的人都听说过进化算法(遗传算法,基因算法)。一篇文章当然不可能把进化算法的方方面面都说清楚,因此,本文只会介绍进化算法的原理,流程,以及少许应用。最主要的是在学习算法时,我自己的一些思考。
一、什么是进化算法
顾名思义,进化算法是模拟生物在自然界中的进化。达尔文的进化论指出“物竞天择,适者生存”。进化论几乎可以解释一切“为什么这种生物是这样的?”这一类的问题。那些更加适应环境的生物,更加容易留下自己的染色体。于是,在计算机中,我们模拟生物中的选择。我们做一次造物主,决定什么样的“生物”更适应环境,更有权利活下来。那么假想你现在是造物主,你想选择一些生物,需要定一些什么规则呢?大概可以总结成下面四个问题:
1、生物生活在什么样的环境中(换言之,什么样的生物才算是适应环境)。
2、生物繁衍后代的方式。
3、生物的种群的大小。
4、物种是否可以基因突变。
大致的设定好这些规则,就我们可以创造一个“种群”和一个选择它们的环境。
二、进化算法中的概念
1、染色体:染色体决定了“生物”的特征和适应环境的能力。一般,染色体是一串01的编码(这里有一个常犯的误区,并不是说染色体的基本组成单位是0和1,染色体由基因组成,基因由0和1组成,而且基因会因为具体问题的约束而会有固定的基因池,这里不理解没关系,后面会提到)。放在具体问题中时,染色体就是一个问题的可选方案。
2、基因池: 基因池就是基因的可选择范围,例如某个问题的定义域是0~4,我们用三位二进制01串表示。那么基因池有以下基因:|0 0 0 0| |0 0 0 1| |0 0 1 0| |0 0 1 1| |0 1 0 0| 。基因池可以说是问题的定义域,那么类似于|1 1 1 1| 这样的基因不属于基因池的基因不会出现在进化算法过程中。理由很简单,假设我们研究猴子的遗传病的时候,有只猴子有个基因突变,变成了人,那就没有研究意义了。
3、适应性函数:适应性函数可以说是进化算法的核心。它决定了上文中写得“规则”中的第一点。什么样的生物才算适应环境。适应性函数就是我们这些造物主筛选优势物种的过滤网。染色体输入到适应性函数中,函数就会输出染色体对环境的适应程度。我们用适应度这个量化概念来描述。
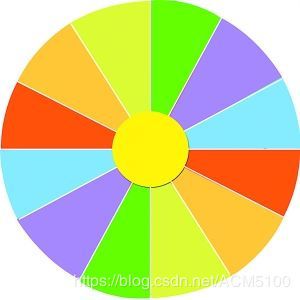
4、选择:就像自然界中一样,每个生物都有繁衍后代的可能性。但是越是适应环境的染色体,留下来的可能性越大。所以适应度越高的物种的染色体,越有可能性被选择。就像是轮盘选择,轮盘上面有一个指针和多个分割的扇形,我们摆动指针,最后指针指向哪一个扇形我们就选择哪一个生物的染色体来繁衍。适应度越高的物种,在轮盘中占得面积越大,自然被选择的可能性越大。
5、交叉:交叉就是染色体之间的基因交换。之前提到的染色体是一串01编码,交叉行为便是决定一个染色体断裂点(和第一点提到的误区一样,染色体可以断裂但是基因不可以断裂,因为基因断裂可能会产生基因池里没有的基因),两个染色体的断裂点相同。每个染色体断裂成两段之后,交换其中一段,从而产生两个新的染色体,替换掉原来的两个染色体。
6、突变:如果之前的描述是可以理解的,你可能发现无论怎么选择,群种当中的染色体组合方式是有限的,因为基因从整体上没有变化(很多基因池中的基因,都未曾出现在这个种群中)。也就是说,很多的基因组合都不可能出现,那么我们就只能选择出这个种群道中最有优势的染色体(局部最优解),而找不到真正的最优染色体(全局最优解)。我们称这种现象为收敛。为了防止这种情况,我们就需要让种群当中的染色体突变。突变的过程就是染色体上的某个基因变成基因池里的另一个基因。也许突变看上去这是微不足道的,但是生物界的进化正是由这种一点一点微不足道的突变叠加,才进化出了如此高级的物种。那么,需要设置一个突变的概率,在理论上突变的概率越高,进化的越快。顺带一提,突变往往是有害的,特别是在物种繁衍了多代之后,种群的平均适应度越高,突变有害的概率越大。
7、种群的大小:为了方便计算,种群的大小往往不变。新产生的基因替换原来的基因。
8、终止条件:利用限定繁衍代数或者其他的方式,来作为终止进化算法的条件。
三、进化算法的流程
我决定结合一个实际的例子来描述进化算法的流程。我就不画流程图了,因为在应用时,流程图肯定会不一样。
拿出最简单的例子,求函数的最大值。
引用计算机科学丛书《人工智能》里的一个例子,f(x)=15x-x^2,我们要求这个函数的最大值。
那么,x的不同取值,就是染色体。令x为0~15的整数。用01串来表示基因,例如x=5,那么基因就是0101。适应性函数就是函数本身。
1、设置一个种群大小N,交叉概率,突变概率,终止条件。
2、设置适应性函数,这里直接用原函数。
3、随机生成一个大小为N的种群,也就是N个染色体。
4、计算所以染色体的适应度。
5、利用上文提到的轮盘选择出两个染色体(这两个染色体可以相同)。
6、交叉两个染色体
假如选择出来的两个染色体,一个染色体X0为 |0 1 1 0| 另一个X1为 |0 0 0 1| 。随意选择一个交叉点(下划线处)。之前提到的两个染色体的交叉点必须为之一致。
那么X0被分割成 |0 1| 和 |1 0| X1 |0 0| 和 |0 1|
两者交换一段变成 |0 1 0 0| 和 |0 0 1 0| 加入并替换掉原来的X0 和 X1,种群数量不变。
7、上帝摇骰子,每个个体都有几率突变 ,例如 X2 |0 1 0 1| 突变成 |0 1 1 1| 。
重复 4~7的过程,直到算法结束。
四、对于算法的思考
你会不会想问,这么简单的函数,随便分析一下就可以找到其最大值的位置?这当然没错,但是如果函数是下面这种样子的,也许数学方法就没那么好用了。
![]() emmmmmm,这个公式编辑器有点问题,左括号漂到上面意思是括号内的是指数。总之就是很复杂。
emmmmmm,这个公式编辑器有点问题,左括号漂到上面意思是括号内的是指数。总之就是很复杂。
这个函数也可以利用基因算法在求最优解。这里就可以说明白基因和染色体的关系了。x 和 y 是函数的两个参数,一组x 和 y的取值就是染色体,那么x 和 y 就是组成染色体的两个基因。
1、审视基因和染色体
假设取 x 为 0~4 y也为 0~4 。 那么 x 和 y 的基因池都是固定的,那么x 和 y 都用三位01字符串表示。 | 0 0 1 0 0 1| 前面三位和为x 后面三位为 y 。那么在交叉时,我们只能以中间为断点,再次强调,基因不能交叉,因为这样会产生基因池以外的基因。例如 染色体|0 0 1 1 0 0| 和 染色体 |0 1 1 0 1 1| 假设在下划线位置交叉,那么会有一个后代 |0 0 1 1 1 1| 这样,y就超出了定义域。那么也可以理解,所谓的突变,也就是在基因池中选择突变对象。当然,如果我们研究的是极度复杂的工作,例如模拟人脑,那么我们也许可以打破这个规则。
2、基因算法可以解决什么问题
基因算法绝对不是仅仅来求个函数的最大值,而是利用可以求最优解这个特性来寻找很多优化问题的解。确定参数,就是基因算法的作用。基因算法的作用就是不停的寻找更加优秀的参数,那么说回来,也就是求一个适应性函数的最优参数。换言之,假如我们可以把具体问题转化成适应性函数,那么就可以利用基因算法求解。
另外我们在利用基因算法的时候,其实我们很难预设一个答案,加入我们想要解决的问题过于的复杂,那么最后问题的答案会是什么样子,我们一概不知。
3、基因算法的基础研究—模式定理
在深入研究基因算法的数学基础时,必定会碰到模式定理。它可以用来描述某种特定染色体的行为,在未来的学习中,这也是值得人们探究和发展的一门学问。
基因算法就写到这里,写的不好不对的地方,欢迎批评指正(别凶我QAQ)。