2016暑期集训16C星座
星座
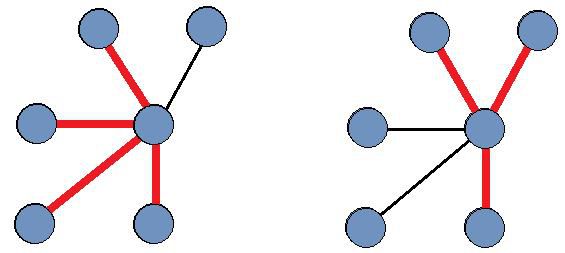
星空中有n颗星星,有n-1对星星间被人为地连上了线,每条连线有各自的长度。所有星星被连成了一个整体。现在,你要在星系中找到一个最大的十字形星座。即,你要找到两条星星构成的路径,使得它们恰好有一颗公共星(这颗公共星不能是某条路径的端点),且两条路径的长度和最大。
左图红线表示了一个合法的十字形星座,而右图的星座并不合法。
输入
第一行一个数n,表示星星的数量。
接下来n行,每行3个数x,y,z,表示第x颗星星和第y颗星星间有一条连线,它的长度是z。
输出
一行,包含一个整数,表示最大的路径长度和。若答案不存在,输出-1。
样例输入
10
3 8 6
9 3 5
1 9 2
4 8 6
2 3 3
10 4 8
5 9 5
7 2 3
6 9 1
样例输出
33
提示
20%的数据n<=1000
50%的数据n<=10,000
100%的数据n<=100,000,0<=z<=1000
其实自己静下来做一做还是简单的
这里的f与g数组十分jingmiao
20% 枚举公共点,求出它每个出度方向上到其它点的最长路径长度,取前4长的加起来。
50% 其实暴力是能过50%的数据的,只要在枚举公共点时先判断一下出度是否大于4即可。这是为了告诉大家就算写暴力也要把必要的优化加上。
100% 任选一个树根,DP,f[i,0..3]分别表示从i开始,向下走到某个叶子为止最长、第二长、第三长、第四长的路径长度。从叶子向树根的顺序DP,每次用f[i,0]去尝试更新i的父亲,可以很方便地求出f数组。用g[i]表示以i为起点,第一步向i的父亲方向走的最长路径长度。第一步从i走到i的父亲fa[i]后,第二步有两种选择, 第一种是继续往父亲走,则最长长度为g[fa[i]],第二种是向下走。为了使路径最长 首选当然是f[fa[i],0],但如果i处在f[fa[i],0]对应的那条路径上,那就只能选择f[fa[i],1]了。有了f数组和g数组后,枚举公共点i,答案为max{f[i,0]+f[i,1]+f[i,2]+f[i,3] , g[i]+f[i,0]+f[i,1]+f[i,2]}。
#include0] && f[y][0]+z>=f[x][1])
{
f[x][3]=f[x][2];
f[x][2]=f[x][1];
f[x][1]=f[y][0]+z;
}
else if (f[y][0]+z1] && f[y][0]+z>=f[x][2])
{
f[x][3]=f[x][2];
f[x][2]=f[y][0]+z;
}
else if (f[y][0]+z>=f[x][3]) f[x][3]=f[y][0]+z;
}
}
void dfs2(int x,int pre)
{
for (int i=head[x];i!=-1;i=Next[i])
{
int y=to[i],z=len[i];
if (y==pre) continue;
if (b[x]==y)
g[y]=max(g[x],f[x][1])+z;
else
g[y]=max(g[x],f[x][0])+z;
dfs2(y,x);
}
}
int main()
{
scanf("%d",&n);
for (int i=1;i<=n;i++)
head[i]=-1;
for (int i=1;iint x,y,z;
scanf("%d%d%d",&x,&y,&z);
du[x]++;
du[y]++;
add(x,y,z);
add(y,x,z);
}
dfs(1,-1);
dfs2(1,-1);
for (int i=1;i<=n;i++)
if (du[i]>=4)
{
ans=max(ans,max(f[i][0]+f[i][1]+f[i][2]+f[i][3],g[i]+f[i][0]+f[i][1]+f[i][2]));
}
printf("%d\n",ans);
return 0;
}