红黑树的理解
在JDK8中,为了防止HashMap出现最坏的情况
如果某个桶中的记录过 大的话(当前是TREEIFY_THRESHOLD = 8),HashMap会动态的使用一个专门的treemap实现来替换掉它。这样做的结果会更好,是O(logn),而不是糟糕的O(n)。它是如何工作 的?前面产生冲突的那些KEY对应的记录只是简单的追加到一个链表后面,这些记录只能通过遍历来进行查找。但是超过这个阈值后HashMap开始将列表升 级成一个二叉树,使用哈希值作为树的分支变量,如果两个哈希值不等,但指向同一个桶的话,较大的那个会插入到右子树里。如果哈希值相等,HashMap希 望key值最好是实现了Comparable接口的,这样它可以按照顺序来进行插入。这对HashMap的key来说并不是必须的,不过如果实现了当然最 好。如果没有实现这个接口,在出现严重的哈希碰撞的时候,你就并别指望能获得性能提升了。
这个性能提升有什么用处?比方说恶意的程序,如果它知道我们用的是哈希算法,它可能会发送大量的请求,导致产生严重的哈希碰撞。然后不停的访问这些 key就能显著的影响服务器的性能,这样就形成了一次拒绝服务攻击(DoS)。JDK 8中从O(n)到O(logn)的飞跃,可以有效地防止类似的攻击
这个性能提升有什么用处?比方说恶意的程序,如果它知道我们用的是哈希算法,它可能会发送大量的请求,导致产生严重的哈希碰撞。然后不停的访问这些 key就能显著的影响服务器的性能,这样就形成了一次拒绝服务攻击(DoS)。JDK 8中从O(n)到O(logn)的飞跃,可以有效地防止类似的攻击
以上这段转载自http://www.cnblogs.com/interdrp/p/3706056.html
下面这段转载自 http://blog.csdn.net/very_2/article/details/5722682
红黑树是二叉查找树的一种,它每个结点都被标上了颜色(红色或黑色),红黑树满足以下5个性质:
1、 每个结点的颜色只能是红色或黑色。
2、 根结点是黑色的。
3、 每个叶子结点都带有两个空的黑色结点(被称为黑哨兵),如果一个结点n的只有一个左孩子,那么n的右孩子是一个黑哨兵;如果结点n只有一个右孩子,那么n的左孩子是一个黑哨兵。
4、 如果一个结点是红的,则它的两个儿子都是黑的。也就是说在一条路径上不能出现相邻的两个红色结点。
5、 对于每个结点来说,从该结点到其子孙叶结点的所有路径上包含相同数目的黑结点。
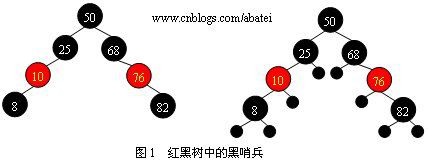
红黑树的这5个性质中,第3点是比较难理解的,但它却非常有必要。我们看图1中的左边这张图,如果不使用黑哨兵,它完全满足红黑树性质,结点50到两个叶结点8和叶结点82路径上的黑色结点数都为2个。但如果加入黑哨兵后(如图1右图中的小黑圆点),叶结点的个数变为8个黑哨兵,根结点50到这8个叶结点路径上的黑高度就不一样了,所以它并不是一棵红黑树。
上面这张图就是想解释第3点性质的作用,假如说,没有第3点的话,光看左图,是满足第5点性质的,但是这样的树结构是不合红黑树的实际要求的,所以加了第3点性质,来规范红黑树
红黑树上结点的插入
在讨论红黑树的插入操作之前必须要明白,任何一个即将插入的新结点的初始颜色都为红色。这一点很容易理解,因为插入黑点会增加某条路径上黑结点的数目,从而导致整棵树黑高度的不平衡。但如果新结点父结点为红色时(如图2所示),将会违返红黑树性质:一条路径上不能出现相邻的两个红色结点。这时就需要通过一系列操作来使红黑树保持平衡。
下面这些图引自于http://blog.csdn.net/v_JULY_v/article/details/6105630
当插入或删除节点,这时红黑树的性质有可能被破坏,所以要重新对节点进行着色与旋转操作(旋转操作其实就是改变指针的指向)
旋转有左旋与右转,
1.左旋
上图其实是Y节点进行左旋操作,即向左移动,由红黑树左小右大的性质可知,当Y节点向左移动时,取代pivot成为该子树的根节点,而pivot成为Y的左节点(因为Y本来就比pivot节点大),Y原先的右节点C保持不变,那Y原先的b节点呢?要放在哪?如果是Y-b-pivot这样的结构呢?这样的结构有个问题就是pivot是b的左节点还是右节点?因为这样的结构下,b只有pivot这一个节点,所以还是如上图那样,b成为了pivot的右节点(表示比pivot大)
2.右旋
同样的,Y节点向右移动
还有种叫双旋,无非就是先左旋再右旋或者先右旋再左旋
左旋右旋的原理知道了,那什么时候该进行左旋右旋,什么时候不用进行?
下面这段话引自 http://www.cnblogs.com/abatei/archive/2008/11/17/1335031.htm
每插入一个结点后,首先检查是否破坏了树的平衡性,如果因插入结点而破坏了二叉查找树的平衡,则找出离插入点最近的不平衡结点,然后将该不平衡结点为根的子树进行旋转操作,我们称该不平衡结点为旋转根,以该旋转根为根的子树称为最小不平衡子树,怎么判断哪个结点是最不平衡结点?
AVL树中的每个结点都有一个平衡因子(balance factor,以下用BF表示),它表示这个结点的左、右子树的高度差,也就是左子树的高度减去右子树的高度的结果值。AVL树上所有结点的BF值只能是-1、0、1。反之,只要二叉树上一个结点的BF的绝对值大于1,则该二叉树就不是平衡二叉树
虽然红黑树不是AVL树,但我觉得也可以用这套理论来理解,只要是红黑树上,这个结点的左树减右树的高度差的绝对值大于1,这个节点就是不平衡结点,就要进行旋转操作
我刚才看到一段话,通过对任何一条从根到叶子的路径上各个结点着色方式的限制,红黑树确保没有一条路径会比其它路径长出俩倍,就在想,要是某个子树的节点全都是黑色的呢?又想到这是不可能的,因为所有新生节点都是红色的(除了根节点),我想,又为了防止某个子树的节点全都是红色的,所以才加了红节点的子节点不能是红色这个要求,因为有了这个要求,红节点才有变成黑色节点的可能(重新着色)
为了清楚地表示插入操作以下在结点中使用“新”字表示一个新插入的结点;使用“父”字表示新插入点的父结点;使用“叔”字表示“父”结点的兄弟结点;使用“祖”字表示“父”结点的父结点。插入操作分为以下几种情况:
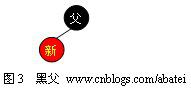
1、黑父
如图3所示,如果新点的父结点为黑色结点,那么插入一个红点将不会影响红黑树的平衡,此时插入操作完成。红黑树比AVL树优秀的地方之一在于黑父的情况比较常见,从而使红黑树需要旋转的几率相对AVL树来说会少一些。
2.红父
如果新点的父结点为红色,这时就需要进行一系列操作以保证整棵树红黑性质。如图3所示,由于父结点为红色,此时可以判定,祖父结点必定为黑色。这时需要根据叔父结点的颜色来决定做什么样的操作。青色结点表示颜色未知。由于有可能需要根结点到新点的路径上进行多次旋转操作,而每次进行不平衡判断的起始点(我们可将其视为新点)都不一样。所以我们在此使用一个蓝色箭头指向这个起始点,并称之为判定点。
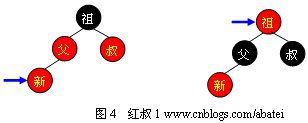
2.1 红叔
当叔父结点为红色时,如图4所示,无需进行旋转操作,只要将父和叔结点变为黑色,将祖父结点变为红色即可。但由于祖父结点的父结点有可能为红色,从而违反红黑树性质。此时必须将祖父结点作为新的判定点继续向上进行平衡操作。
需要注意,无论“父”在“叔”的左边还是右边,无论“新”是“父”的左孩子还是右孩子,它们的操作都完全一样。
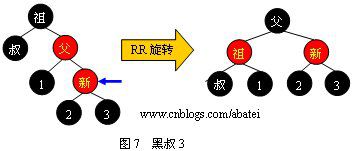
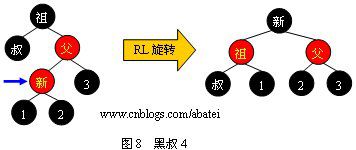
2.2 黑叔
当叔父结点为黑色时,需要进行旋转,以下图示了所有的旋转可能
这就是为什么要考虑叔父结果颜色的原因了,因为叔父结点是黑色的话,你再改变原来父节点的颜色,就会产生我们上面说的不平衡结点,因为原本父节点是红色的,现在要重新着色成黑色,那就意味着父节点这边的子树多了父节点这一个黑结点,那就打破平衡了
LL意思是新节点插在根节点的左孩子树的左子树里,RR,LR,RL同样道理
情形1:直接右旋再重新着色
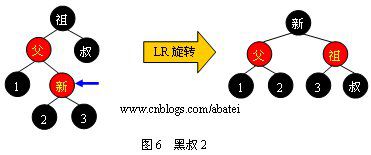
情形2:先左旋再右旋然后重新着色,先左旋就变成情况1那样子,然后像情况1那样右旋就好了
情形3:左旋再重新着色
情形4:先右旋再左旋,然后重新着色,
可以观察到,当旋转完成后,新的旋转根全部为黑色,此时不需要再向上回溯进行平衡操作,插入操作完成。需要注意,上面四张图的“叔”、“1”、“2”、“3”结点有可能为黑哨兵结点。
其实红黑树的插入操作不是很难,甚至比AVL树的插入操作还更简单些。但删除操作就远远比AVL树复杂得多,下面就介绍红黑树的删除操作。
先了解下二叉树的几个名词 先序 中序 后序 前驱 后继
树的遍历的三种情况,是根据左子树、右子树、根这3者的不同访问次序来定义的。
根左右(根先访问),则为先序遍历
左根右,则为中序遍历;
左右根,则为后序遍历
例如:求下面树的三种遍历
前序遍历:abdefgc
中序遍历:debgfac
后序遍历:edgfbca
拿中序来讲,为什么中序遍历的顺序是debgfac,我们要将上图分成几部分来看就理解了,首先 d-e是一个子树 g-f是一个子树,e-d-b-f-g是一个子树,因为中序是先从左子树取然后就是根然后才轮到右子树,d-e这个子树是整个大树中最左的,所以先从这取起,因为d-e没有左树,所以先从d这个根取起,de,然后从e-d-b-f-g这个子树来讲,左边的子树d-e已经取了,轮到根了,那就是b,所以就是deb,然后根取完了,就轮到右边这个子树了,在右边子树g-f中,g是左子树,所以先取,那就是debg了,然后左子树取完取中,即f,那就是debgf,之后的逻辑就是这样推了
前驱结点:节点val值小于该节点val值并且值最大的节点
后继节点:节点val值大于该节点val值并且值最小的节点
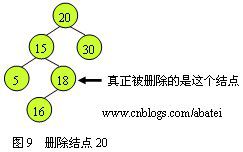
回归到红黑树的删除操作
在二叉查找树中删除一个给定的结点p有三种情况
(1) 结点p无左右子树,则直接删除该结点,修改父节点相应指针
(2) 结点p有左子树(右子树),则把p的左子树(右子树)接到p的父节点上
(3) 左右子树同时存在,则有三种处理方式
a. 找到结点p的中序直接前驱结点s,把结点s的数据转移到结点p,然后删除结点s,由于结点s为p的左子树中最右的结点,因而s无右子树,删除结点s可以归结到情况(2)。严蔚敏数据结构P230-231就是该处理方式。
b. 找到结点p的中序直接后继结点s,把结点s的数据转移到结点p,然后删除结点s,由于结点s为p的右子树总最左的结点,因而s无左子树,删除结点s可以归结到情况(2)。算法导论第2版P156-157该是该处理方式。
c. 找到p的中序直接前驱s,将p的左子树接到父节点上,将p的右子树接到s的右子树上,然后删除结点p。