Transformer-XL模型：Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context
参考链接
参考论文:https://arxiv.org/abs/1901.02860
参考博客:https://ai.googleblog.com/2019/01/transformer-xl-unleashing-potential
摘要
- Transformer网络具有学习更长期依赖性的潜力，但这种潜力往往会受到上下文长度固定 的限制。因此，我们提出了一种叫做 Transformer-XL 的新神经架构来解决这一问题，它可以在不破坏时间一致性的情况下，让Transformer超越固定长度学习依赖性。具体来说，它是由片段级的循环机制和全新的位置编码策略组成的。我们的方法不仅可以捕获更长的依赖关系，还可以解决上下文碎片化的问题。Transformer-XL 学习到的依赖性比RNN学习到的长80%，比Vanilla Transformer学到的长 450%，无论在长序列还是短序列中都得到了更好的结果，而且在评估时比Vanilla Transformer快 1800+ 倍。此外，我们还提升了bpc 和困惑度的当前最佳结果，在 enwiki8 上 bpc 从 1.06 提升至 0.99，在 text8 上从 1.13 提升至 1.08，在 WikiText-103 上困惑度从 20.5 提升到 18.3，在 One Billion Word 上从 23.7 提升到 21.8，在宾州树库（不经过微调的情况下）上从 55.3 提升到 54.5。我们的代码、预训练模型以及超参数在 TensorFlow 和 PyTorch 中都可以使用。
- 注意：论文Character-level language modeling with deeper self-attention中的Transform而称为Vanilla Transformer
模型架构
- 语料库中的样本表示为 x = ( x 1 , x 2 , … , x T ) x=(x_1,x_2,…,x_T ) x=(x1,x2,…,xT)；语言模型的任务是估计联合概率分布 P ( x ) P(x) P(x)；通过因式分解可以将联合概率分布分解为条件概率分布的乘积，即： P ( x ) = ∏ t P ( x t ∣ x < t ) P(x)=∏_tP(x_t |x_{<t}) P(x)=∏tP(xt∣x<t)；这样语言模型的任务变成评估条件概率分布；我们使用神经网络对条件概率进行建模，具体说就是：使用一个可训练的神经网络将上下文 x < t x_{<t} x<t编码到固定大小的隐藏层状态中去，然后将隐藏层状态乘以词embeding矩阵得到logits，再将logits经过一个softmax函数，得到下一个词的概率分布.
Vanilla Transformer Language Models
- 将Transformer应用于语言模型，关键的一点就是：如何训练Transformer有效的将任意长度的上下文编码到固定大小的 表示(expression) 中去。
- 若给定无限的存储和计算，一个简单的解决方案是：使用无条件的Transformer处理整个上下文序列，类似于前馈神经网络。但这一般情况下是不可行的。
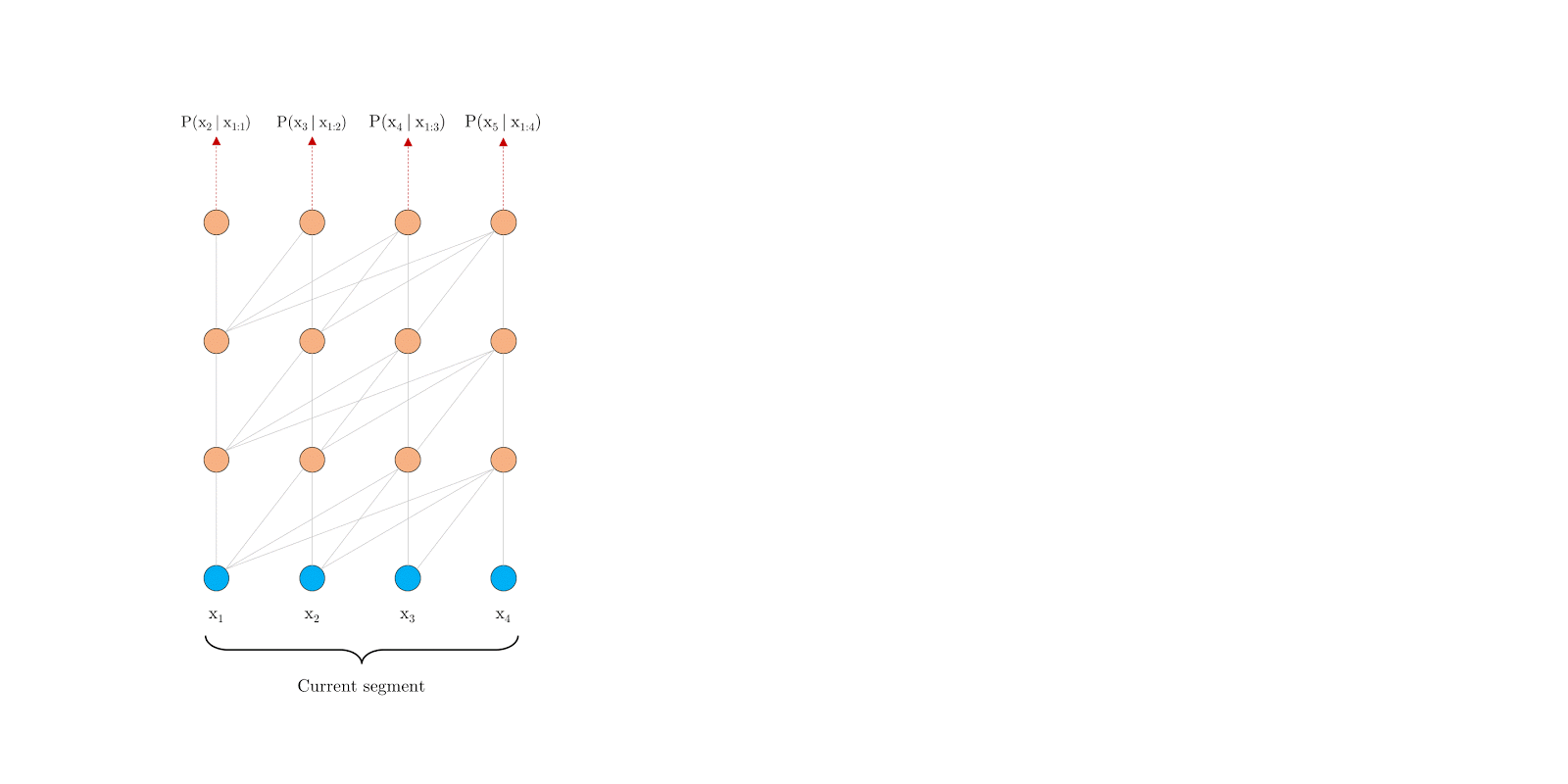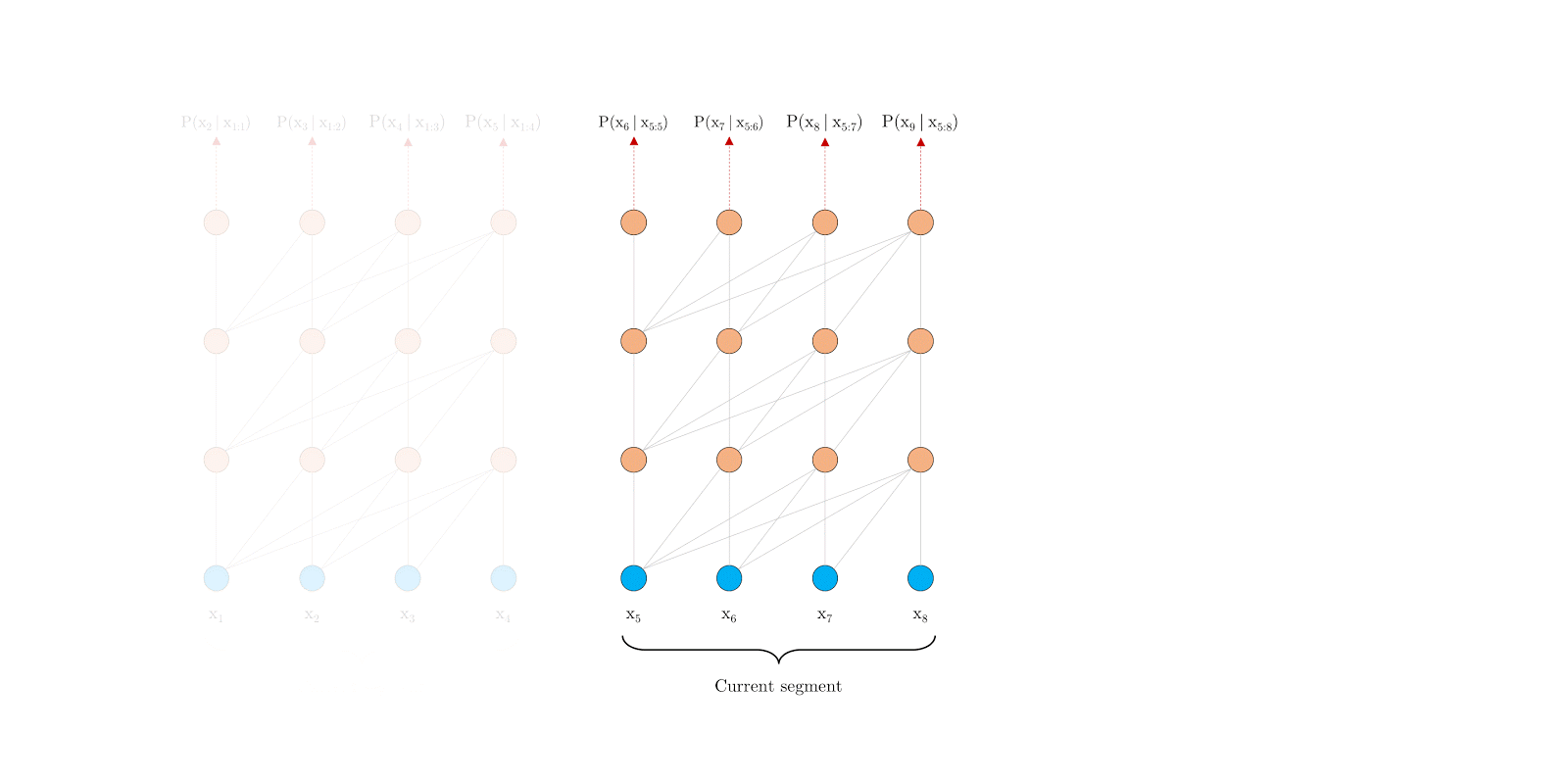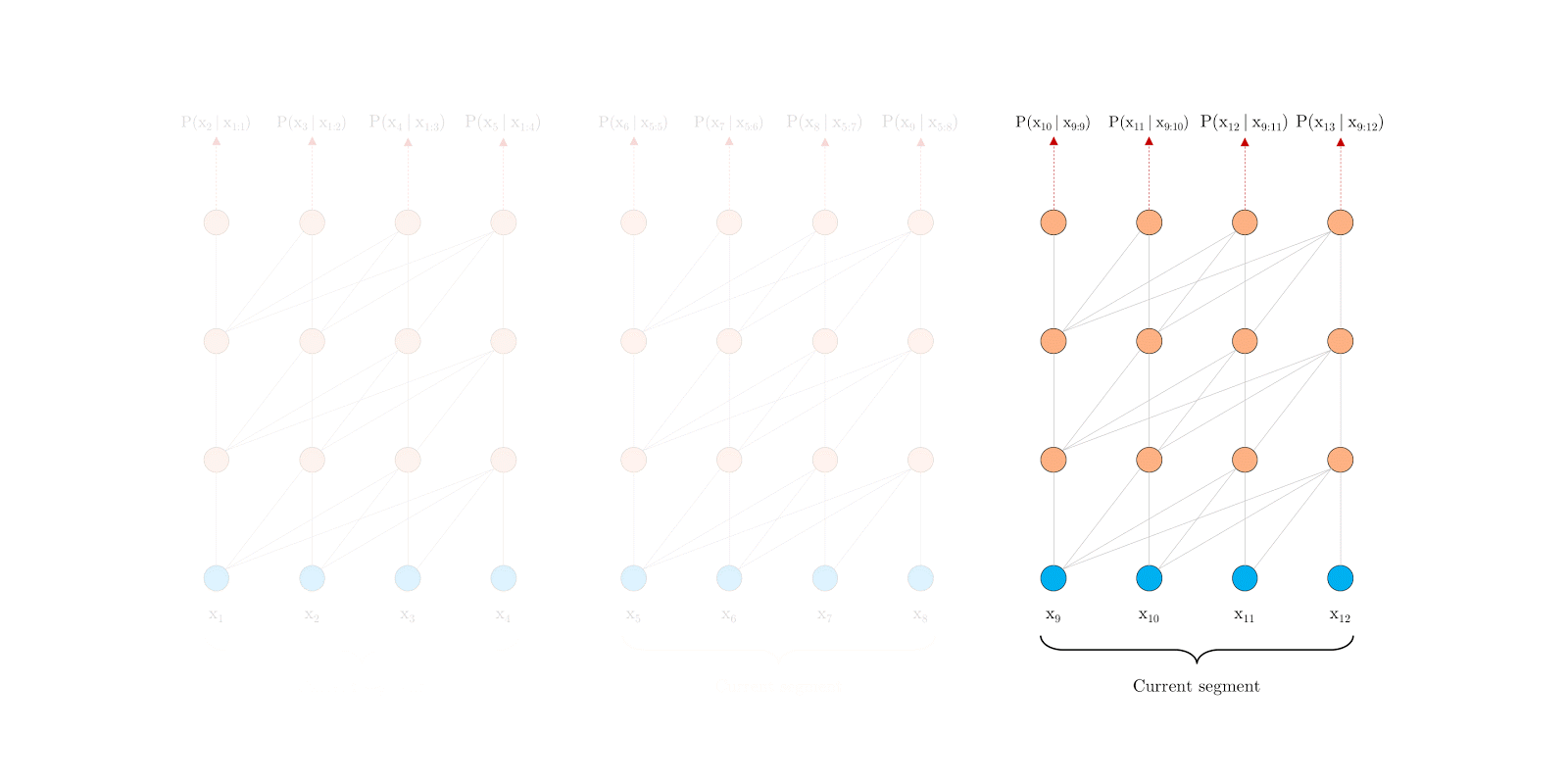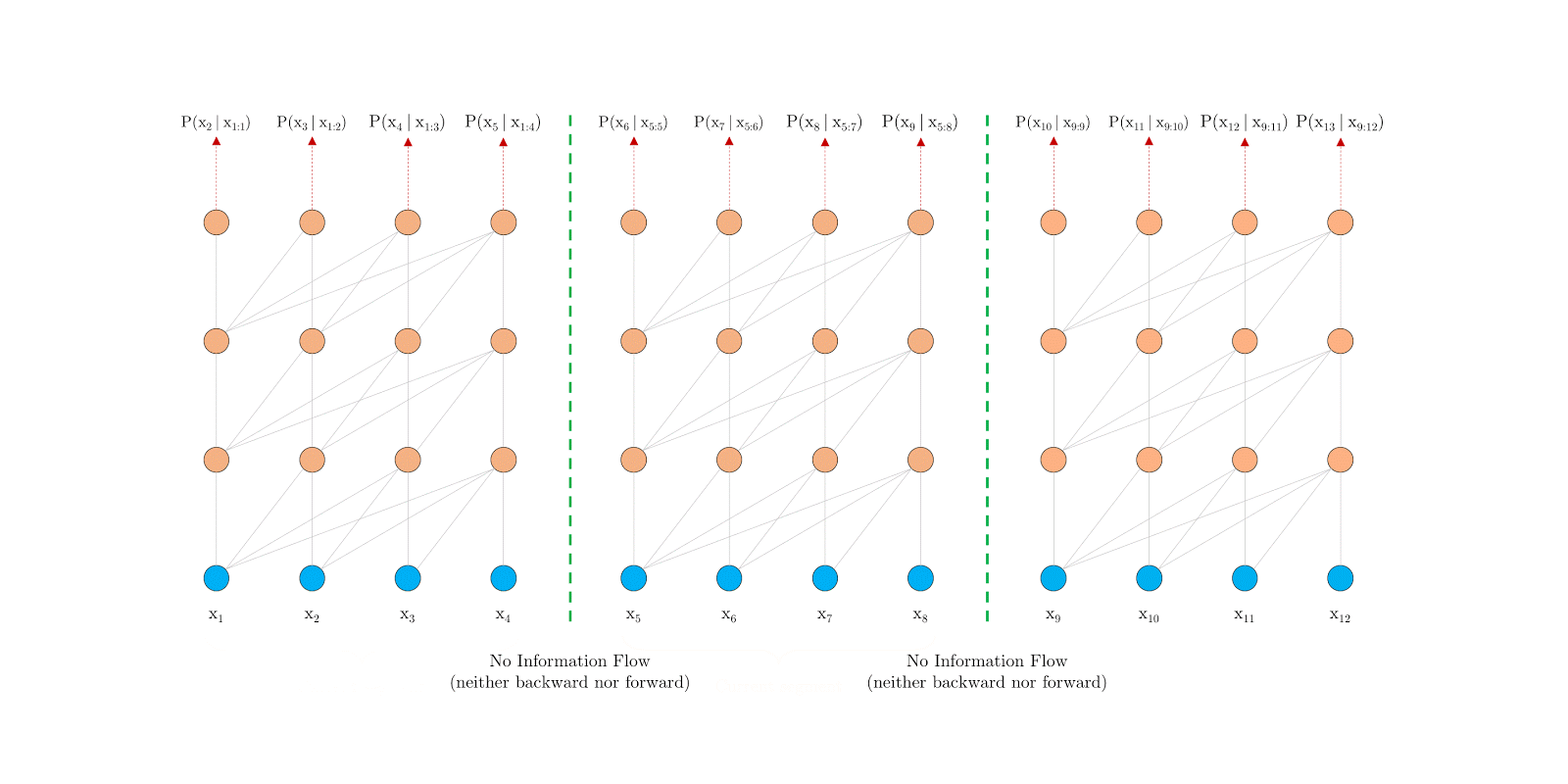
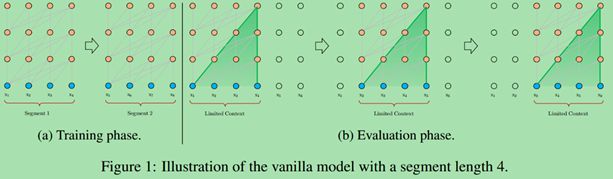
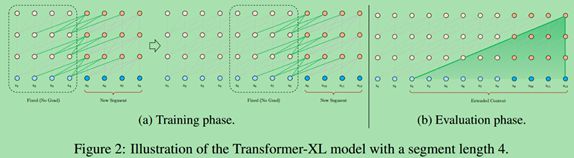
- 一个近似的方法：将整个语料库切分为更短的段，并且仅仅在每个段内进行训练，在每个段中忽略前一个段的信息。这是论“Character-level language modeling with deeper self-attention”中的做法，称改论文中的Transformer为Vanilla Transformer如下图所示：
- 使用固定长度段进行训练时的两个问题：
- 模型可能很大程度上依赖段长的最大值。
- 将长文本简化为固定长度的段将导致上下文断裂(context fragmentation)问题
- 在评估阶段，每一步在预测下一个词时都需要从新计算可获得的最大长度的上下文信息。这样可以解决训练阶段的下文断裂问题，但计算量巨大。
Segment-Level recurrence state reuse
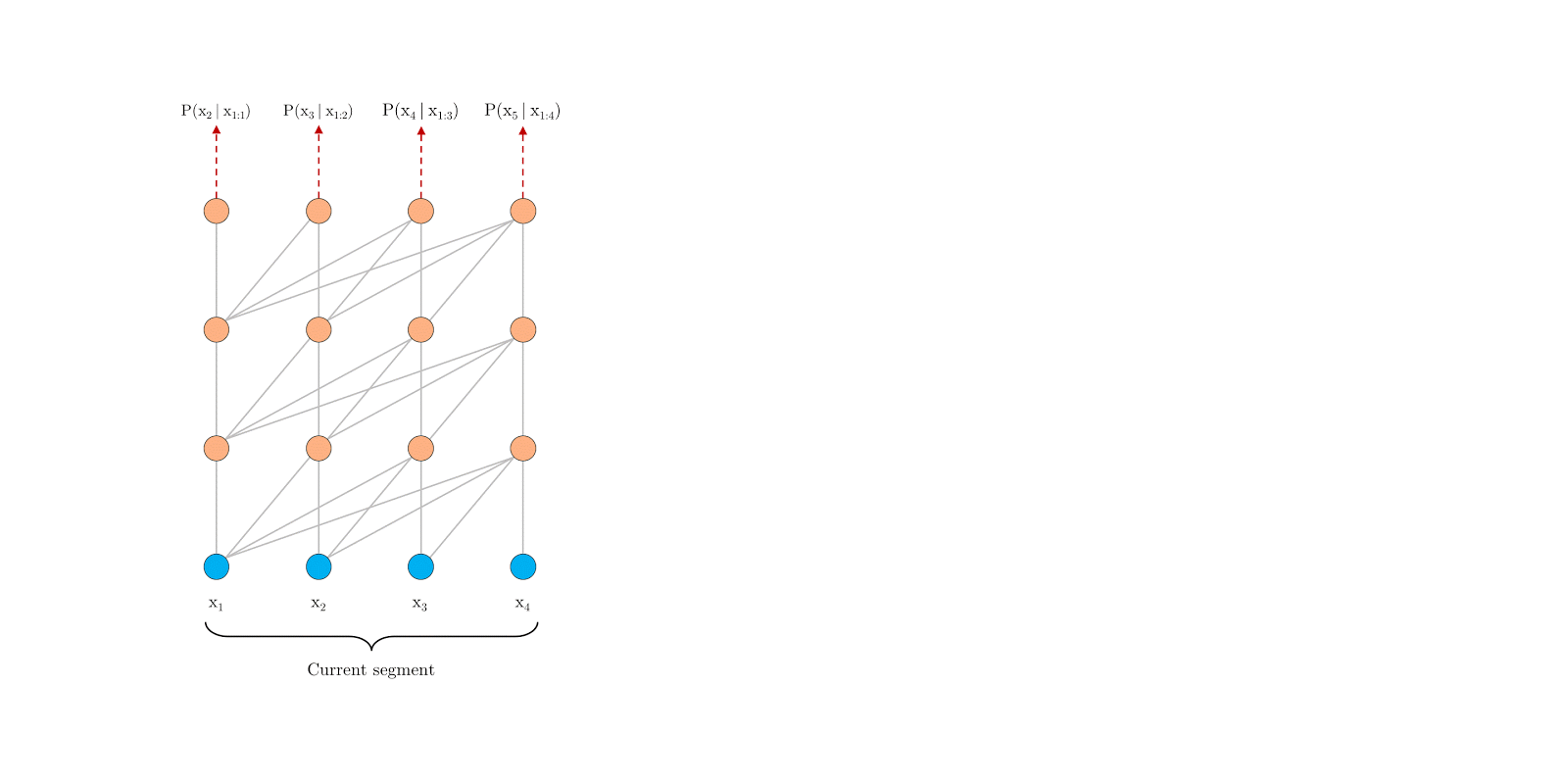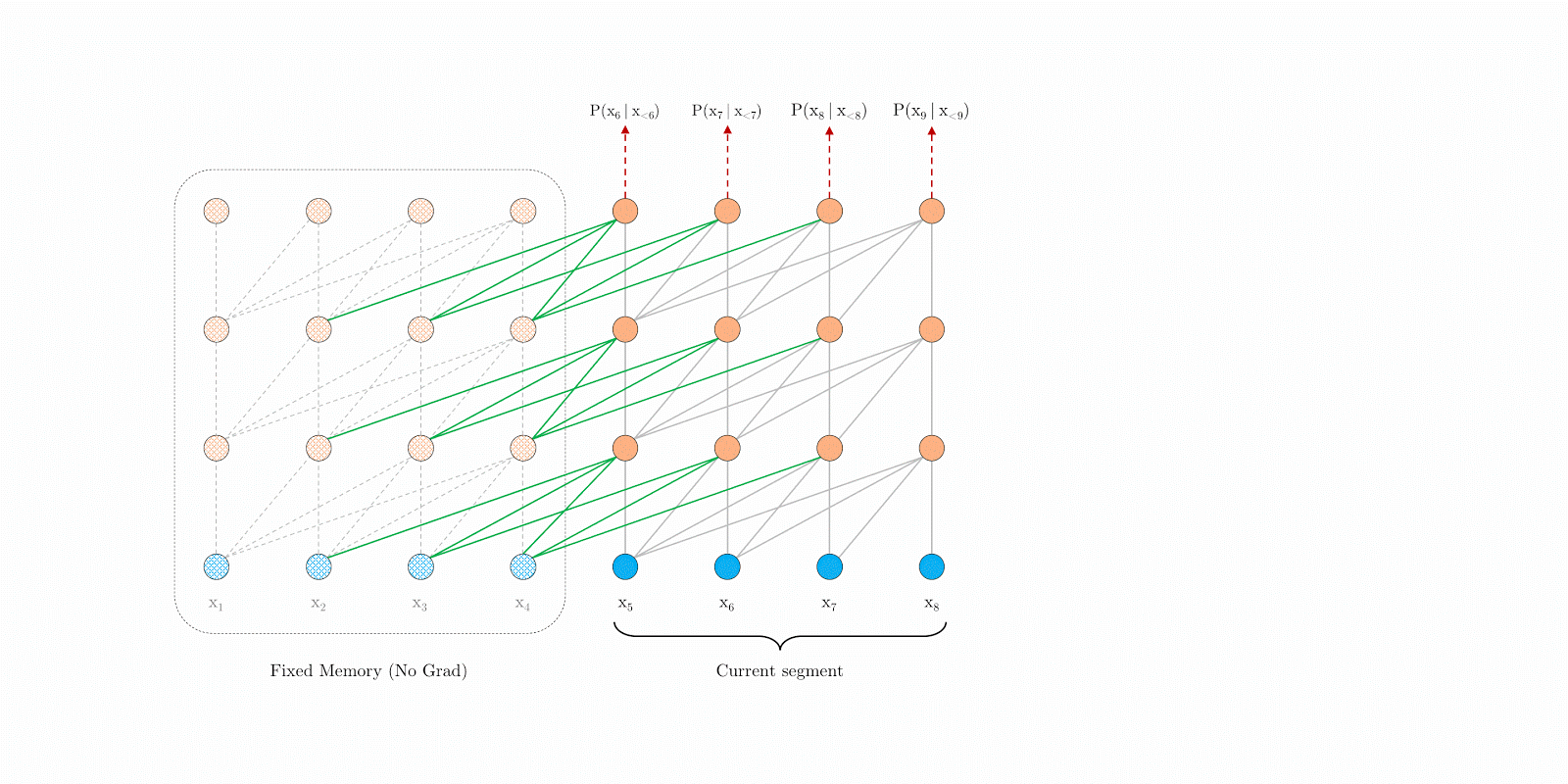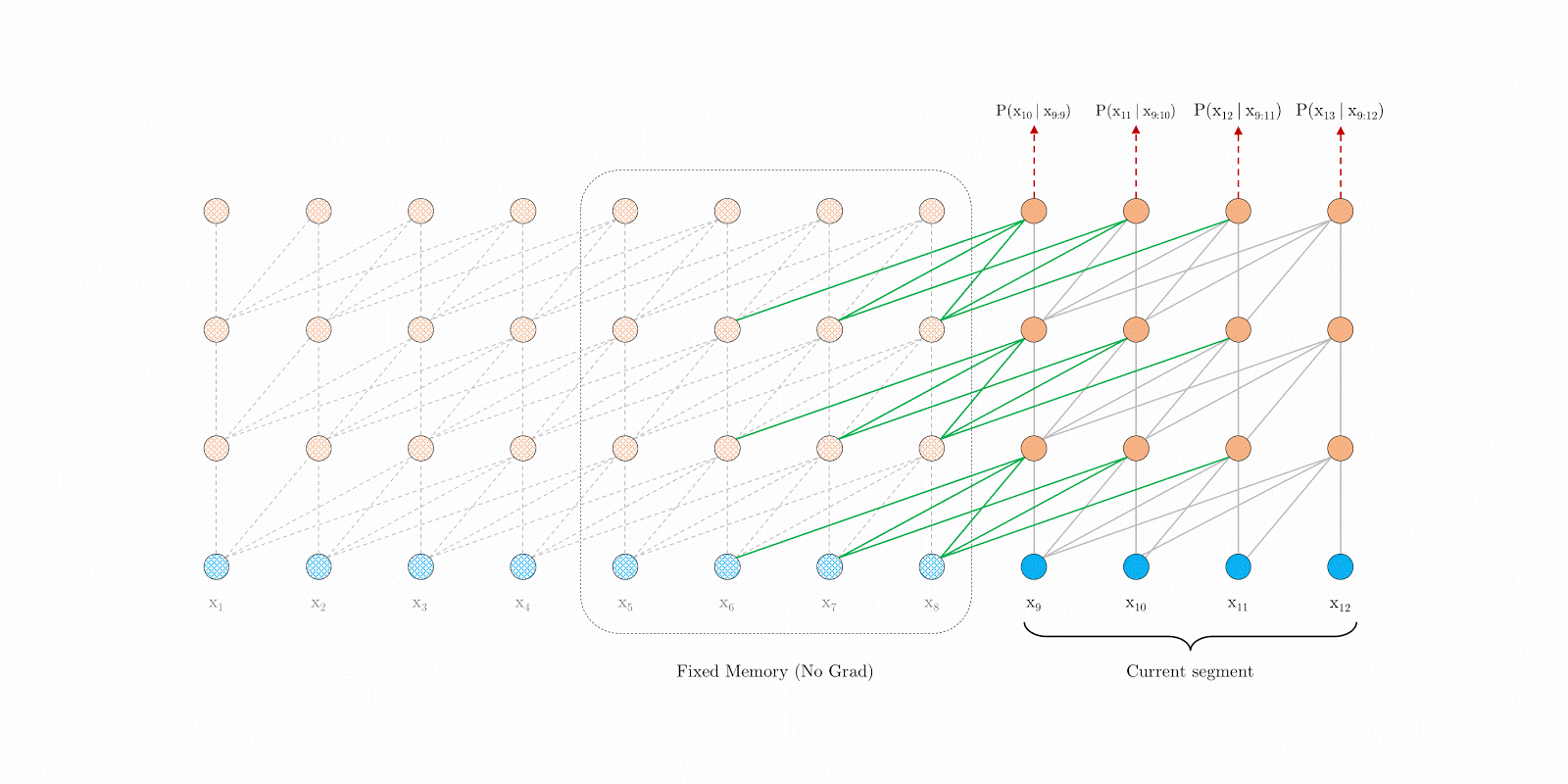
- 为了解决固定长度上下文的限制，我们提出在Transformer体系结构中引入循环机制。下图是这种模型的结构图：
- 在训练期间，处理每个段后，我们将其所以固定长度隐藏层状态序列存储起来，用来在处理下一段时作为上下文信息扩展。但是从图上我们可以看到：每个位置都只拿其前面segment_length个词的隐藏层状态向量做上下文信息。但是我们知道这个范围的隐藏层状态向量也包含了前面不再这个范围的上下文信息，因此它能够建模长期依赖信息，并且避免上下文碎片。
- 公式表示如下：
- 令：段长为L;相邻的两个段为： S t = [ x t , 1 , x t , 2 , … , x t , L ] S_t=[x_{t,1},x_{t,2},…,x_{t,L}] St=[xt,1,xt,2,…,xt,L]和 S t + 1 = [ x t + 1 , 1 , x t + 1 , 2 , … , x t + 1 , L ] S_{t+1}=[x_{t+1,1},x_{t+1,2},…,x_{t+1,L}] St+1=[xt+1,1,xt+1,2,…,xt+1,L]; S t S_t St的产生的第n层的隐藏层状态序列为： h t n ∈ R L × d h_t^n∈R^{L×d} htn∈RL×d， d d d是隐藏层的维度；然后 S t + 1 S_{t+1} St+1的第 n n n层的隐藏层序列计算公式如下：
其中： S G ( ⋅ ) SG(·) SG(⋅)表示梯度停止(stop-gradient), [ h u ◦ h v ] [hu◦hv] [hu◦hv]表示隐藏层状态序列的拼接； W W W标售的是模型的参数
- 令：段长为L;相邻的两个段为： S t = [ x t , 1 , x t , 2 , … , x t , L ] S_t=[x_{t,1},x_{t,2},…,x_{t,L}] St=[xt,1,xt,2,…,xt,L]和 S t + 1 = [ x t + 1 , 1 , x t + 1 , 2 , … , x t + 1 , L ] S_{t+1}=[x_{t+1,1},x_{t+1,2},…,x_{t+1,L}] St+1=[xt+1,1,xt+1,2,…,xt+1,L]; S t S_t St的产生的第n层的隐藏层状态序列为： h t n ∈ R L × d h_t^n∈R^{L×d} htn∈RL×d， d d d是隐藏层的维度；然后 S t + 1 S_{t+1} St+1的第 n n n层的隐藏层序列计算公式如下：
- 这个循环机制被应用到语料库中的每两个相邻的段上，这本质上是一个段级的循环机制。
- 从模型图上我们可以看到段之间的上下文信息是每经过一段会向上传递一层，因此最大可能的依赖长度随模型层数和段长线性增长，就像上图的b部分一样。
- 循环架构带来的另一个好处就是加快的模型验证的速度。
- 循环架构仅限于相邻两段之间。理论上，在GPU内存允许的条件下，可以缓存多个先前段的隐藏层状态序列，并在处理当前段时将所有段重用为额外的上下文。 在论文的实验中训练期间只缓存一段，在测试期间缓存多段。同时我们将缓存的序列统一记为： m t n ∈ R M × d m_t^n∈R^{M×d} mtn∈RM×d其中M是段长的倍数。
Relative position encodings
- 为了使用缓存的历史隐藏层状态信息，我们还需要解决一个关键的问题：在我们使用这些缓存的历史信息时，如何保持连贯的位置信息。这会使我们回想起标准的Transformer，它是使用位置编码来表示序列中字符的位置信息，具体的做法是使用一个位置编码矩阵 U ∈ R L m a x × d U∈R^{L_{max×d}} U∈RLmax×d,矩阵的第 i i i行表示的就是句子中的第 i i i个词的决定位置信息， L m a x L_max Lmax表示的是最大句子长度，最后Transformer的输入是词embeding和位置embeding的逐元素的和。如果我们简单的将这个思想使用到我们的模型中可以得到下面的公式： h t + 1 = f ( h t , E s t + 1 + U 1 : L ) h_{t+1}=f(h_t,E_{s_{t+1} }+U_{1:L} ) ht+1=f(ht,Est+1+U1:L) h t = f ( h t − 1 , E s t + U 1 : L ) h_t=f(h_{t-1},E_{s_t }+U_{1:L} ) ht=f(ht−1,Est+U1:L)其中： E s t ∈ R L × d 为 s t E_{s_t }∈R^{L×d}为s_t Est∈RL×d为st的embeding矩阵。 f f f为Transformation函数， U 1 : L U_{1:L} U1:L为位置 1 − L 1-L 1−L的编码。
- 由上面公式我们可以看出 E s t + 1 E_{s_{t+1}} Est+1和 E s t E_{s_t} Est使用相同的位置编码 U 1 : L U_{1:L} U1:L，这会导致模型无法区分 x t , j x_{t,j} xt,j和 x t + 1 , j x_{t+1,j} xt+1,j的位置。
- 为了避免上面的问题，基本思想是仅对隐藏状态的相对位置信息进行编码。不是将位置embeding静态地加入到词embeding中去，而是将位置embeding信息加入到每层的注意力分数中去，即将embeding信息加入到每层隐藏层状态序列中去。
- 例如，当查询(query)向量 q t , i q_{t,i} qt,i去关注(attends)key向量 k t , ≤ i k_{t,≤i} kt,≤i时，它不需要知道每个key向量的绝对位置，相反它只要知道每个key相邻与自己的相对距离就ok了。
- 实际上，可以创建一个相对位置编码 R ∈ R L m a x × d R∈R^{L_{max}×d} R∈RLmax×d矩阵，其中第 i i i行表示两个位置之间相对距离为 i i i。通过将相对距离动态地注入关注分数(attention score)中，查询向量可以容易地区分 x t , j x_{t,j} xt,j和 x t + 1 , j x_{t+1,j} xt+1,j，因为它们相对查询向量的距离不一样。这样使得状态重用机制可行。
- 对于标准的Transformer，注意力分数的计算公式如下：
A i , j a b s = q i T k j A_{i,j}^{abs}=q_i^T k_j Ai,jabs=qiTkj = E x i T W q T W k E x j + E x i T W q T W k U j + U i T W q T W k E x j + U i T W q T W k U j =E_{x_i}^T W_q^T W_k E_{x_j }+E_{x_i}^T W_q^T W_k U_j+U_i^T W_q^T W_k E_{x_j }+U_i^T W_q^T W_k U_j =ExiTWqTWkExj+ExiTWqTWkUj+UiTWqTWkExj+UiTWqTWkUj = [ W q ( E x i + U i ) ] T ∗ [ W k ( E x j + U j ) ] =[W_q (E_{x_i }+U_i )]^T*[W_k (E_{x_j}+U_j)] =[Wq(Exi+Ui)]T∗[Wk(Exj+Uj)] - 我们修改后的Transformer，注意力分数的计算公式如下： A i , j r e l = E x i T W q T W k , E E x j + E x i T W q T W k , R R i − j + u T W k , E E x j + v T W k , R R i − j A_{i,j}^{rel}=E_{x_i}^T W_q^T W_{k,E} E_{x_j }+E_{x_i}^T W_q^T W_{k,R} R_{i-j}+u^T W_{k,E} E_{x_j }+v^T W_{k,R} R_{i-j} Ai,jrel=ExiTWqTWk,EExj+ExiTWqTWk,RRi−j+uTWk,EExj+vTWk,RRi−j = ( E x i T W q T + u T ) ( W k , E E x j ) + （ E x i T W q T + v T ） ( W k , R R i − j ) =(E_{x_i}^T W_q^T+u^T )(W_{k,E} E_{x_j } )+（E_{x_i}^T W_q^T+v^T ）(W_{k,R} R_{i-j} ) =(ExiTWqT+uT)(Wk,EExj)+（ExiTWqT+vT）(Wk,RRi−j) = ( W q E x i + u ) T ( W k , E E x j ) + （ W q E x i + v T ( W k , R R i − j ) =(W_q E_{x_i }+u)^T (W_{k,E} E_{x_j} )+（W_q E_{x_i }+v^T (W_{k,R} R_{i-j} ) =(WqExi+u)T(Wk,EExj)+（WqExi+vT(Wk,RRi−j)
- 其中R是正弦编码的矩阵，是不可学习的参数。并且 W q E x i , u , v , W k , E E x j , W k , R R i − j W_q E_{x_i },u,v,W_{k,E} E_{x_j },W_{k,R} R_{i-j} WqExi,u,v,Wk,EExj,Wk,RRi−j一般都是长度相同的列向量，这点需要注意。
- 这里我们将key向量的线性映射矩阵写成了两部分： W k , E ， W k , R W_{k,E}，W_{k,R} Wk,E，Wk,R,分别来生成词embeding的key向量和相对位置的embeding的key向量。
- 我们使用可训练的uT和vT向量代替查询词x_i的位置embeding的查询向量： W q U i W_q U_i WqUi，原因：询词 x i x_i xi对于待询词 x j x_j xj是一样的,因此 x i x_i xi位置已经不重要了。
所以：对所有的查询 x i x_i xi向量，使用同一个可以训练的向量 [ u , v ] [u,v] [u,v]来替代 x i x_i xi的位置embeding的生成的查询向量： W q U i W_q U_i WqUi - 整个模型的公式总结： h ^ t n − 1 = [ S G ( m t n − 1 ) ∗ h t n − 1 ] \hat{h}_t^{n-1}=[SG(m_t^{n-1} )*h_t^{n-1}] h^tn−1=[SG(mtn−1)∗htn−1] q t n , k t n , v t n = h t n − 1 W q n T , h ^ t n − 1 W k , E n T , h ^ t n − 1 W v n T q_t^n ,k_t^n ,v_t^n=h_t^{n-1} W_q^{n^T},\hat{h}_t^{n-1} W_{k,E}^{n^T},\hat{h}_t^{n-1} W_v^{n^T} qtn,ktn,vtn=htn−1WqnT,h^tn−1Wk,EnT,h^tn−1WvnT A t , i , j n = q t , i n T k t , j n + q t , i n T W k , R n R i − j + u T k t , j n + v T W k , R n R i − j A_{t,i,j}^n=q_{t,i}^{n^T} k_{t,j}^n+q_{t,i}^{n^T} W_{k,R}^n R_{i-j}+u^T k_{t,j}^n+v^T W_{k,R}^n R_{i-j} At,i,jn=qt,inTkt,jn+qt,inTWk,RnRi−j+uTkt,jn+vTWk,RnRi−j a t n = M a s k e d − S o f t m a x ( A t n ) v t n a_t^n=Masked-Softmax(A_t^n ) v_t^n atn=Masked−Softmax(Atn)vtn 0 t n = L a y e r N o r m ( L i n e a r ( a t n ) + h t n − 1 ) 0_t^n=LayerNorm(Linear(a_t^n)+h_t^{n-1}) 0tn=LayerNorm(Linear(atn)+htn−1) h t n = P o s i t i o n w i s e − F e e d − F o r w a r d ( 0 t n ) h_t^n=Positionwise-Feed-Forward(0_t^n) htn=Positionwise−Feed−Forward(0tn)其中 h t 0 = E s t h_t^0=E_{s_t} ht0=Est
个人的理解：
- 对于标准的Transformer，我们将词embeding+绝对位置embeding输入到Transformer，在输入后不再向Transformer添加任何的位置信息。
- Transformer-XL模型并不是这样的，它在每一层输入时，都会将input(第0层为词embeding)+相对位置embeding输入到Transformer-XL的上一层，但是相对位置embeding是不可训练的。
- 为了更好的理解该模型我改写上面的公式：
- 个张量的维度如下：
- h t n ∈ R L × d , m t n ∈ R M × d h_t^n∈R^{L×d},m_t^n∈R^{M×d} htn∈RL×d,mtn∈RM×d每一行一个词
- h ^ t n − 1 ∈ R ( M + L ) × d \hat{h}_t^{n-1}∈R^{(M+L)×d} h^tn−1∈R(M+L)×d
- q t n ∈ R L × d 1 ; k t n , v t n ∈ R M + L × d 1 ; W q n , W k , E n , W k , R n , W v n ∈ R d 1 × d q_t^n∈R^{L×d_1 };k_t^n ,v_t^n∈R^{M+L×d_1 };W_q^n,W_{k,E}^n,W_{k,R}^n,W_v^n∈R^{d_1×d} qtn∈RL×d1;ktn,vtn∈RM+L×d1;Wqn,Wk,En,Wk,Rn,Wvn∈Rd1×d
- R i − j = R ∈ R L m a x × d R_{i-j}=R∈R^{L_{max}×d} Ri−j=R∈RLmax×d 第 ( i − j ) (i-j) (i−j)行
- u , v ∈ R d u,v∈R^d u,v∈Rd
- A t n ∈ R L × ( L + M ) A_{t}^n\in R^{L×(L+M)} Atn∈RL×(L+M)
- 根据上面维度的假设, A t , i , j n A_{t,i,j}^n At,i,jn公式如下： A t , i , j n = q t , i n k t , j n T + q t , i n ( R i − j W k , R n T ) T + u k t , j n T + v ( R i − j W k , R n T ) T A_{t,i,j}^n=q_{t,i}^n k_{t,j}^{n^T} +q_{t,i}^n (R_{i-j}W_{k,R}^{n^T})^T+u k_{t,j}^{n^T}+v (R_{i-j} W_{k,R}^{n^T})^T At,i,jn=qt,inkt,jnT+qt,in(Ri−jWk,RnT)T+ukt,jnT+v(Ri−jWk,RnT)T其中这个式子中的每一项都是一个实数， A t , i , j n A_{t,i,j}^n At,i,jn表示的是当前位置的词 x i x_i xi对上下文 x j x_j xj的attention 分数。下面给出矩阵运算： A t n = q t n k t n T + q t n ( R i − j W k , R n T ) T + u k t n T + v ( R i − j W k , R n T ) T A_{t}^n=q_{t}^n k_{t}^{n^T} +q_{t}^n (R_{i-j}W_{k,R}^{n^T})^T+u k_{t}^{n^T}+v (R_{i-j} W_{k,R}^{n^T})^T Atn=qtnktnT+qtn(Ri−jWk,RnT)T+uktnT+v(Ri−jWk,RnT)T A t n A_{t}^n Atn是L×(L+M)的矩阵，即 A t n ∈ R L × ( L + M ) A_{t}^n\in R^{L×(L+M)} Atn∈RL×(L+M)
- 现在为了更好的理解我们将 W k , E n 和 W k , R n W_{k,E}^n和W_{k,R}^n Wk,En和Wk,Rn，统一为 W k n W_k^n Wkn；并且令 u = v = z W q n T u=v=zW_q^{n^T} u=v=zWqnT,则可以得到： A t , i , j n = ( h t , i n − 1 W q n T + z W q n T ) T [ ( h ^ t , j n − 1 W k , E n T ) + ( R i − j W k , R n T ) ] = [ ( h t , i n − 1 + z ) W q n T ] T [ ( h ^ t , j n − 1 + R i − j ) W k n T ] A_{t,i,j}^n=(h_{t,i}^{n-1} W_q^{n^T}+zW_q^{n^T} )^T [(\hat{h} _{t,j}^{n-1} W_{k,E}^{n^T} )+(R_{i-j} W_{k,R}^{n^T})] =[(h_{t,i}^{n-1}+z) W_q^{n^T}]^T [(\hat{h}_{t,j}^{n-1}+R_{i-j} ) W_k^{n^T} ] At,i,jn=(ht,in−1WqnT+zWqnT)T[(h^t,jn−1Wk,EnT)+(Ri−jWk,RnT)]=[(ht,in−1+z)WqnT]T[(h^t,jn−1+Ri−j)WknT]这个公式可以理解为：在每一层输入时当前词 x i x_i xi加上一个全局的位置embeding z z z,改词前面的词都加上一个相对位置embeding，然后输入Transform。
- 个张量的维度如下：